Изучение алгоритма сортировки Шелла. Обменная сортировка (сортировка методом «пузырька»)

1.  Цель

Изучение алгоритма сортировки Шелла.

2.  Вариант задания №9.

Сортировка Шелла. Частичную сортировку с заданным шагом, начиная с заданного элемента оформить в виде функции. Алгоритм частичной сортировки - обменная (методом «пузырька»).

3.  Теория

Обменная сортировка (сортировка методом «пузырька»)

Суть ее заключается в следующем: производится попарное сравнение соседних элементов 0-1,1-2 и т.д. и перестановка, если пара расположена не в порядке возрастания. Просмотр повторяется до тех пор, пока перестановок больше не будет. Метод получил свое название за то, что "более весомые" элементы сдвигаются в процессе сортировки к концу массива.

Сортировка разделением.

Сортировки, основанные на принципе разделения массива разделяют его на две части относительно некоторого значения, называемого медианой. Сами части не упорядочены, но обладают таким свойством, что элементы в левой части меньше медианы, а элементы правой - больше. Благодаря такому свойству эти части можно сортировать независимо. Для этого нужно вызвать ту же самую функцию сортировки, но уже не по отношению к массиву, а к его частям. Функции, вызывающие сами себя, называются рекурсивными. Рекурсивный вызов продолжается до тех пор, пока очередная часть массива не станет содержать единственный элемент.

Сортировка подсчетом.

Путем сравнения всех пар элементов массива для каждого из них подсчитывается количество элементов, меньших его. Это дает новое местоположение этого элемента в выходном массиве.

Сортировка выбором.

В массиве выбирается меньший элемент из 0...n и обменивается с нулевым. Затем то же самое повторяется с элементами от 1 до n-1 и т.д.

Сортировки вставками.

Простая вставка: определяется место в отсортированной части массива, куда должен помещаться элемент. Элементы от данной позиции сдвигаются вверх и на освободившееся место помещается элемент.

Вставка погружением: очередной элемент путем ряда обменов “погружается” до требуемой позиции в уже упорядоченную часть массива.

Сортировка Шелла.

Существенными в сортировках вставками (или обмена) являются затраты на обмены или сдвиги элементов. Для их уменьшения желательно сначала производить погружение с большим шагом, сразу определяя элемент «по месту», а затем делать точную «подгонку». Так поступает сортировка Шелла: исходный массив разбивается на m частей, в каждую из которых попадают элементы с шагом m, начиная от 0,1,...,m-1 соответственно, то есть

  0 , m  , 2m  , 3m  ,...

  1 , m+1, 2m+1, 3m+1,...

  2 , m+2, 2m+2, 3m+2,...

Каждая часть сортируется отдельно с использованием алгоритма вставок. Затем выбирается меньший шаг, и алгоритм повторяется. Шаг может быть выбран равным степеням 2, например 64,32,16,8,4,2,1. В данном случае я выбрал шаг равный n/2.

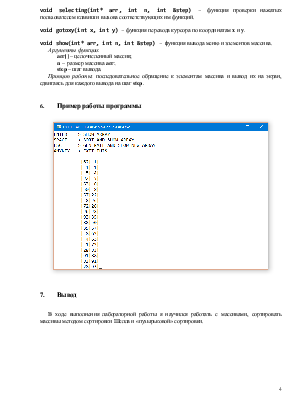
4.  Анализ задачи и алгоритм

1)  Анализ задачи

Входные данные: целочисленный массив, сформированный случайным образом.

Результат: упорядоченный массив.

Метод решения: сортировка Шелла.

2)  Алгоритм решения задачи

·  Формирование массива;

·  Задаём начальные границы сортировки (нулевой и последний элементы);

·  Определяем шаг, с которым массив будет делиться на части;

·  Сортируем эти части с помощью сортировки «Пузырёк»;

·  Вывод отсортированного массива.

5.  Описание программной реализации

1) Используемые переменные

arr[] – исходный массив (int);

n – размер массива (int);

k – индекс начала сортировки по группам (int);

m – шаг сортировки (int);

tmp – переменная – третий стакан (int);

keyb – символьная переменная (char), в которую функция getch() возвращает код нажатой пользователем клавиши;

step – очередной шаг вывода на экран (int).

2) Используемые функции

voidgen(int* arr, intn) – функция формирования массива.

Аргументы функции:

arr[] – целочисленный массив;

n –  размер массива arr.

Принцип работы: с помощью библиотечной функции rand() генерируется случайное число и присваивается очередному элементу массива arr[].

void sortShell(int* arr, int n) – функция сортировки  Шелла.

Аргументы функции:

arr[] – целочисленный массив;

n –  размер массива.

Принцип работы: два вложенных цикла предназначены для передачи в функцию bubble() значений шага сортировки m и индекса начала пузырьковой сортировки k.

voidbubble(int* arr, intk, intm, intn) – функция обменной сортировки