1. Цель работы
Приобретение навыков реализации алгоритмов ЦОС на отладочном комплекте ADSP-BF533 EZ-KIT Lite на примере систем дискретной фильтрации
2. Краткие теоретические сведения.
2.1. Описание КИХ-фильтров
Дискретный фильтр — это произвольная система обработки дискретного сигнала, обладающая свойствами линейности и стационарности. Линейность означает, что выходная реакция на сумму сигналов равна сумме реакций на эти сигналы, поданные на вход по отдельности, а стационарность — что задержка входного сигнала приводит лишь к такой же задержке выходного сигнала, не меняя его формы. Любой фильтр обладает определенной частотной характеристикой. Чтобы она была нетривиальной, то есть, чтобы коэффициент передачи фильтра на разных частотах был разным, выходной сигнал фильтра y(k) должен зависеть от нескольких отсчетов входного сигнала x(k). Таким образом, дискретный фильтр должен обладать памятью.
Чтобы обеспечить линейность и стационарность, производимые фильтром математические операции должны ограничиваться сложением и умножением на константы.
Уравнение фильтрации для КИХ-фильтра выглядит следующим образом.
![]() (2.1)
(2.1)
Из формулы видно, что в вычислении выходного отсчета фильтра принимают участие только входные отсчеты, но не используются предыдущие выходные. Количество используемых коэффициентов и предыдущих отсчетов m называется порядком фильтра. Структурная схема, реализующая формулу (2.1), приведена на рис. 2.1. Некоторое количество предыдущих отсчетов входного сигнала хранится в ячейках памяти, которые образуют дискретную линию задержки. Эти отсчеты умножаются на коэффициенты bi, и суммируются, формируя выходной отсчет y(k).
Так как при вычислениях не используются предыдущие отсчеты выходного сигнала, в схеме отсутствуют обратные связи. Поэтому такие фильтры называются нерекурсивными (nonrecursive). Применяется также термин «трансверсальный фильтр» (от английского transversal — поперечный).
Импульсная характеристика нерекурсивного цифрового фильтра (НЦФ) определяется очень просто. Подставим в уравнение (2.1) единичный импульс x0(k) в качестве входного сигнала:
![]() (2.2)
(2.2)
Но отсчет x0(k – i) равен нулю для всех k, кроме k = i, когда этот отсчет равен единице. Поэтому мы получаем очень простой результат:
![]() (2.3)
(2.3)
То есть коэффициенты bi, являются отсчетами импульсной характеристики фильтра. Это можно наглядно пояснить с помощью рис. 2.1. При подаче на вход единичного импульса он будет перемешаться по линии задержки, умножаться на коэффициенты b0, b1, b2 … и проходить на выход устройства (ведь все остальные входные сигналы сумматора при этом равны нулю).
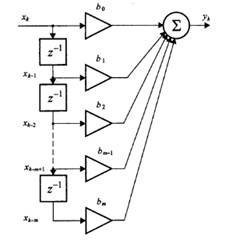
Рис. 2.1. Нерекурсивный фильтр
Очевидно, что в реальном устройстве линия задержки содержит конечное число элементов, поэтому импульсная характеристика нерекурсивного фильтра также является конечной по длительности. Это обусловило еще одно название таких фильтров — фильтры с конечной импульсной характеристикой (КИХ-фильтры; английский термин — finite impulse response, FIR).
Вследствие отсутствия обратных связей, любой нерекурсивный фильтр является устойчивым — ведь каковы бы ни были начальные условия (то есть отсчеты, хранящиеся в линии задержки), при отсутствии сигнала на входе (x(k) = 0) выходной сигнал (свободные колебания) будет отличен от нуля в течение не более чем m тактов, необходимых для очистки линии задержки.
Простота анализа и реализации, а также наглядная связь коэффициентов фильта с отсчетами его импульсной характеристики и абсолютная устойчивость привели к тому, что нерекурсивные фильтры широко применяются на практике. Однако для получения хороших частотных характеристик (например, полосовых фильтров с высокой прямоугольностью АЧХ) необходимы нерекурсивные фильтры высокого порядка – до нескольких сотен и даже тысяч.
2.2. Описание программы, реализующей алгоритм нерекурсивного фильтра
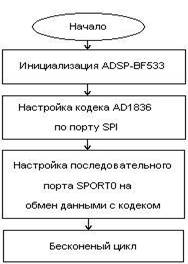
Алгоритм демонстрационной программы реализации КИХ-фильтра приведен на рис. 2.2
Алгоритм работы КИХ-фильтра
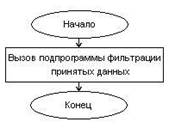
Прерывание по приему данных SPORT0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.