Расчет фильтра нижних частот Баттерворта, полосового фильтра Чебышева и активного фильтра

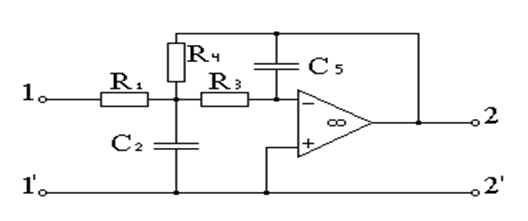
Рассмотрим общие принципы реализации передаточной функции второго порядка

                                     (1)

с помощью ОУ, охваченного обратной связью (ОС). Пассивная часть схемы представляет собой многополюсник, состоящий из резистивных и емкостных элементов (рис.1)

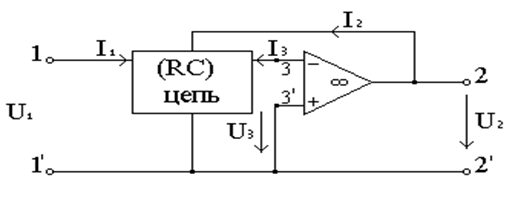Рис.1 Электронная схема на основе ОУ с ОС

Составим уравнение пассивного трехполюсника в Y-форме.

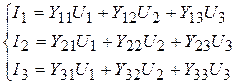                                                                 (2)

При условии идеального ОУ его входная цепь (зажимы 3-3’) не потребляет тока, т.е. I₃ = 0. Учитывая, что U₂ = - K₀U₃, из третьего уравнения системы (2) получим

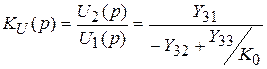 .                                                  (3)

При K ® ¥ передаточная функция цепи определяется только параметрами RC-цепи:

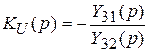  .                                                                       (4)

Предположим, что RC-многополюсник имеет структуру, показанную на рис.2б и состоящую из пяти пассивных компонентов (R-  и C-элементов)

Воспользуемся свойствами идеального ОУ: разность потенциалов между его входными зажимами равна нулю, т.е. U₃ = 0 (см.рис.2). Это означает, что потенциал зажима 3 равен нулю. Составим уравнение узлов 4 и 3:

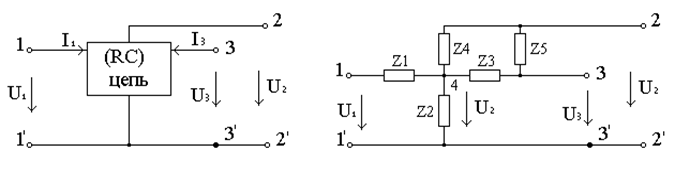
                     а)                                                               б)

Рис.2. Пассивный трехполюсник (а) и его 5-элементная конфигурация (б)

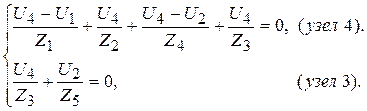
Разрешая второе уравнение этой системы относительно выходного напряжения U₂, т.е. 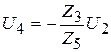, и подставляя результат в первое уравнение, после не сложных преобразований получим выражение для коэффициента передачи по напряжению:

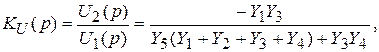                                     (5)

где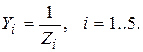

Задавая в качестве проводимостей Y_i проводимость емкости pC_i или проводимость сопротивления 1/R_i, можно составить требуемый вид передаточной функции K_U(p).

1.1  НЧ-фильтр второго порядка. Его передаточная функция имеет вид:

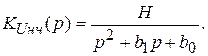                                                              (6)

Чтобы правая часть уравнения (5) соответствовала дроби (6), следует выбрать в качестве ёмкостей элементы Y₂ и Y₅, остальные представить сопротивлениями. Тогда передаточная функция может быть выражена через параметры элементов (RC)-схемы (рис.3):

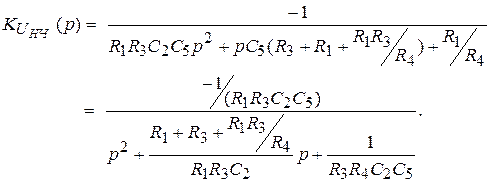     (7)

Таким образом, из сопоставления функций (6) и (7) выводится система из трех уравнений для определения параметров элементов пассивного трехполюсника:

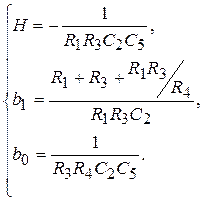                                                     (8)

Поскольку неизвестных параметров пять, то два из них могут задаваться произвольно. Обычно выбирается какая-то ёмкость, например, C₂ = C₀ из нормального ряда параметров и постоянная времени t₀ = R₁C₂, т.е. R₁ = t₀ / C₀. Параметры остальных элементов находятся подстановкой C₂ и R₁ в систему (8) с последующим её решением:

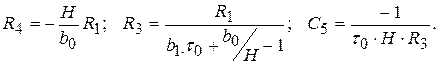                  (9)    

Глава 2. Расчетная часть

                 1. Расчет фильтра нижних частот Баттерворта

Исходные  данные:

·  f₁= 1 кГц

·  ∆A=0.5 Дб

·  f_s=2,5 кГц

·  A_s=30 Дб

·  R_н =500 Ом

1.1Расчет с помощью  таблиц

Определим нормированную частоту:

Ω_s=f_s/f₁ (1.1)

Ω_s=2,5/1=2,5 (1.2)

n=A_s-10lg(10^0.1*∆A-1)/20lg Ω_s (1.3)

n=30-10lg(10^0.05-1)/20lg2,5=30-10*0.049/20*0.39=4.91 (1.4)

округлим это число, увеличивая его  до ближайшего целого и получим n=5

схема фильтра будет следующей:

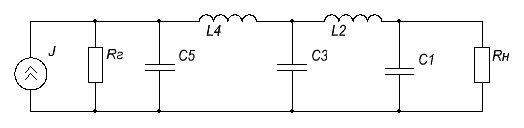
Выпишем из таблицы 9 параметры элементов схемы:

c₁=c₅=0.618

l₂=l₄=1.618

c₃=2

Денормируем эти элементы по следующим схемам:

L= K_l* l  (1.5)    

C= K_l* c (1.6)

Где:

K_l=R_Н/2*π*f₁ (1.7)

K_c=1/R_н*2*π*f₁ (1.8)

K_l=500/6.28*1000=0.07957

 K_c=1/6.28*1000*500=318,3*10^-9

С₁=С₅=0.618*318,3*10^-9=196,7 нФ

L₂=L₄=1.618*0.07957= 128,74 мГн

С₃=2*318,3*10^-9=636,6 нФ

Частота f₀ вычисляется по формуле:

f₀ =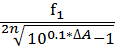

 f₀ =  =  =1234 Гц

Передаточную функцию по напряжению записываем на основании таблицы 7:

H(p)=1/a₅(p)=1/p⁵ + 3.2361p⁴ +5.2361p³ +5.2361p² +3.2361p + 1

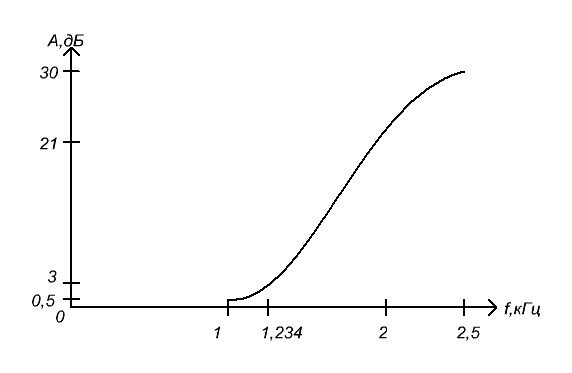
Проведем расчет ослабления фильтра:

A_Ω= 10lg(1+(10^0.1*∆A-1)Ω²ⁿ)

Расчет проведем для частот f₁ ,f₀ , 2f₁ , f_s :

A_f1= 10lg(1+(10^0.1*0.5-1)¹⁰)=0.5 дБ

A_2f1= 10lg(1+(1.122-1)¹⁰) =21 дБ

A_f0= 10lg(1+(10^0.1*0.5-1)¹⁰)=3 дБ

A_fs= 10lg(1+(10^0.1*0.5-1)¹⁰)=30,6 дБ

                                      1.2 Аналитический метод

Вычисляем S_k  для нечетных n по следующей формуле:

S_k=cos (k*π/5) + j*sin(k*π/5)

Где к=1,2,…2n

Выберем те S_k которые имеют отрицательные вещественные части. Это будет при к=3,4,5,6,7.

n=5           k=3

S₃=S₇=cos (3*π/5) + jsin (3*π/5) = -3,09017*10^-1 + j9,5105655*10^-1

n=5           k=4

S₄=S₆=cos (4*π/5) + jsin (4*π/5) = -8,09017*10^-1 + j5,8778529*10^-1

n=5           k=5

S₅= cos (5*π/5) + jsin (5*π/5) = -1

Вычислим знаменатель передаточной функции:

V(S)=(S-S₃)(S-S₇)(S-S₃)(S-S₆)(S-S₅) =(S+3,09017*10^-1 -j9,5105655*10^-1)*(S+3,09017*10^-1 - j9,5105655*10^-1)*(S+8,09017*10^-1 - j5,8778529*10^-1)*(S+8,09017*10^-1 -j5,8778529*10^-1)*(S+1) = S⁵ + 3.23607S⁴ + 5.223607S³ + 5.223607S² + 3.23607S + 1

Из этого выражения видно, что значения совпадают с таблицей 7.

Функция фильтрации h(s) = s⁵.

Вычислим нормированное входное сопротивление, беря верхние знаки:

Z _ВХ=V(S)-h(S)/ V(S) +h(S) = 2S⁵ + 3.23607S⁴ + 5.223607S³ + 5.223607S² + 3.23607S + 1/ 3.23607S⁴ + 5.223607S³ + 5.223607S² + 3.23607S + 1

Разложим полученное в цепную дробь:

а) делим числитель на знаменатель:

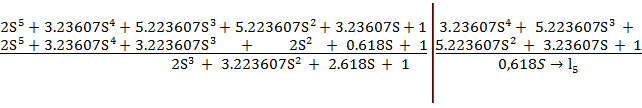
б) делим делитель на первый остаток:

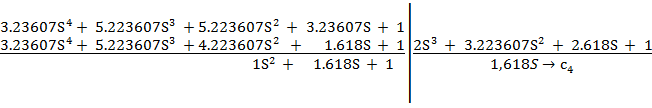
в) делим второй делитель на второй остаток:

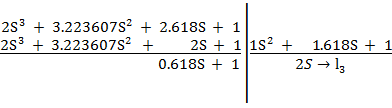
г) делим третий делитель на 3-й остаток:

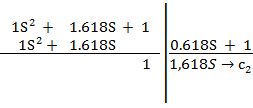
д) делим четвертый делитель на четвертый остаток:

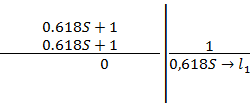
Таким образом, мы получили полное соответствие расчетных значений табличным значениям.

2 Расчет полосового фильтра Чебышева

Исходные данные

·  f_-1=10 кГц

·  f₁=14.4 кГц

·  ∆f=4.4 кГц

·  f_s2=16 кГц

·  A_s2=28 дБ

·  ∆A= 0.5 дБ

Найдем среднюю геометрическую полосу пропускания фильтра:

f₀=

f₁ и f_-1 – граничные частоты полосы пропускания фильтра

f₀===12 кГц

Найдем нормированную частоту фильтра:

Ω_s=k*(f_s/f₀ – f₀/f_s) , где k=f₀/∆f

k=12/4.4=2.72

Ω_s=2.72(16/12 – 12/16)=1.59

определим порядок фильтра:

n≥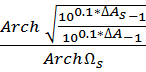

n≥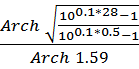==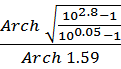==3.84

Итак, порядок фильтра должен быть равен 5. Согласно рис. 7б схема фильтра-прототипа низких частот будет следующей:

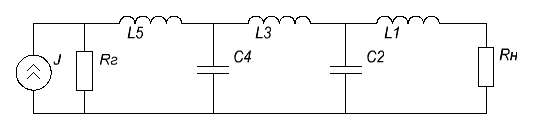
По таблице 10 для ∆A= 0.5 Дб и n=5 нормированные элементы ФПНЧ имеют значения:

l₁=1.706

c₂=1.230

l₃=2.541

c₄=1.230

l₅=1.706

От схемы на рис….. согласно формулам и рисункам 30в, переходим к реальной схеме ПФ путем замены каждого индуктивного элемента последовательным соединением индуктивности l_i индуктивностью l_in=kl_i  и емкостью c_in=1/kl_i , а каждой емкости с_j – заменой параллельным соединением емкости c_jn=kc_j и индуктивности l_jn=1/kc_j :

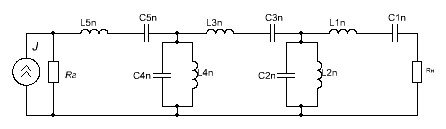
L_1n=L_5n=1.706*2.727=4.65

С_1n=C_5n=1/1.706*2.727=0.215

L_2n=L_4n=1/1.230*2.727=0.298  

C_2n=C_4n=1.230*2.727=3.35

L_3n=2.541*2.727=6.93

C_3n=1/2.541*2.727=0.144

Перейдем к номинальным значениям элементов схемы:

L= K_l* l 

C= K_l* c

Где:

K_l=R_Н/2*π*f₀

K_c=1/R_н*2*π*f₀

L_1n=L_5n=4,65* 0,00663=30,8 мГн

С_1n=C_5n=0.215* 0,02653*10^-6=5,7 нФ

L_2n=L_4n=0.298*0,00663=1,97 мГн

C_2n=C_4n=3,35*0,02653*10^-6=88,8 нФ

L_3n=6,93*0,00663=45,95 мГн

C_3n=0.144*0,02653*10^-6=3,8 нФ

Вычислим затухание фильтра на частотах f₀ ,f_-1 , f₁ , f_s , 2f_s

A=10lg[1+(10^0.1*∆A-1)*Tn²(Ω)]

где

Tn(Ω)=ch(n*Arch Ω)

при f₀=12 кГц

Ω=12/4.4*(12/12-12/12)=0

при f_-1=10 кГц

Ω=12/4.4*(10/12-12/10)=-1

 при f₁=14,4 кГц

Ω=12/4.4*(14,4/12-12/14,4)=1

при f_s=16 кГц

Ω=12/4.4*(16/12-12/16)=1,59

при 2f_s=32 кГц

Ω=12/4.4*(32/12-12/32)=6.25

при 1.5f_s=24 кГц

Ω=12/4.4*(24/12-12/24)=4.09

 =10lg[1+(10^0.1*0.5-1)* (5*Arch 0)]=0 дБ

 =10lg[1+(10^0.1*0.5-1)* (5*Arch 1)]=0.5 дБ

 =10lg[1+(10^0.1*0.5-1)* (5*Arch 1.59)]=30 дБ

 =10lg[1+(10^0.1*0.5-1)* (5*Arch 4.09)]=35 дБ

 =10lg[1+(10^0.1*0.5-1)* (5*Arch 6.25)]=38 дБ

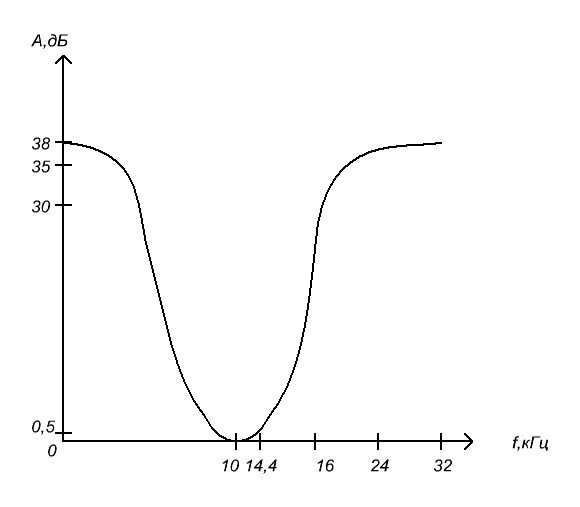
3. Расчет активного фильтра Чебышева

Исходные данные:

f₁=20 кГц

∆A=1 дБ

f_s=30 кГц

A_s=20 дБ

K=10

Прежде всего определим порядок фильтра вычислив его по формуле:

n≥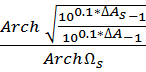

n≥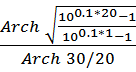==5,0729

Принимаем порядок фильтра равным 6, следовательно, мой фильтр состоит из трех звеньев второго порядка. Коэффициент усиления распределим следующим образом: для первого