Расчет преобразователя двоичного кода в двоично-десятичный на основе делителя, разработка логической схемы

Склеиваются наборы, отличающиеся друг от друга значением одного разряда. Такие наборы называются соседними. Карно закодировал клетки своей карты так, что в соседних клетках оказались соседние, а значит, склеивающиеся наборы. Соседними могут быть не только отдельные клетки, которые мы назовем элементарными квадратами Карно, но и целые группы соседних клеток (назовем их прямоугольниками Карно). Под прямоугольником Карно будем понимать некоторую, зачастую разрозненную фигуру покрытия, все соседние клетки которой закодированы соседними наборами.

Алгоритм графической минимизации логических функции:

1. Заполнить карту Карно нулями и единицами в соответствии с таблицей истинности;

2. Покрыть все единичные наборы минимальным количеством прямоугольников Карно, каждый из которых имеет максимальную площадь.

3. Каждому прямоугольнику Карно соответствует одна импликанта, причем, если в границах прямоугольника Карно какая-либо переменная принимает значения как 0, так и 1, то она склеивается.

Если в карте Карно нулей окажется меньше, чем единиц, то удобнее прямоугольниками Карно покрыть все нулевые наборы. В результате мы получим инверсию минимизируемой функции.

Сущность метода достаточно прозрачна. Стремление к минимальному количеству прямоугольников Карно приводит в результате к минимальному количеству слагаемых в булевой функции. Требование получения максимальной площади прямоугольника Карно вызвано стремлением минимизировать длину каждого слагаемого булевой функции.

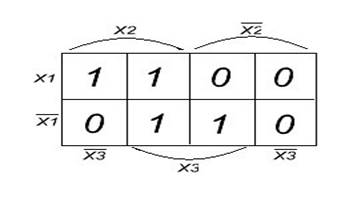
Другим методом минимизации является минимизация с помощью диаграмм Вейча. Правила получения МДНФ с помощью диаграммы Вейча:Все клетки диаграммы Вейча, содержащие единицы объединяются в замкнутые области, при этом каждая область должна представлять собой прямоугольник с числом клеток 2^к  (к=1,2…..n). Области с единицами могут пересекаться и одни и те же клетки могут входить в разные области. При охвате клеток замкнутыми областями следует стремиться, чтобы число их было минимальным. При этом минимальным будет число членов МДНФ логической функции. А каждая область  содержала возможно большее число клеток с единицами. Пример:

y=    +     + _{1  3}  + ₁    

                                                                                               После минимизации получим:   y= ₁  +    

Разработка логической схемы на базе заданной таблицы истинности

Условие первого задания приведено в таблице 1.

Таблица 1.

На основании данных, представленных в таблице истинности выпишем все наборы, на которых функция принимает значение 1 или единичные наборы, которых хватает, чтобы описать функцию Y:

1.  _{4  3    1} =1

2.    =1

3.   =1

    =1

5.    =1 

6.    =1 

7.      =1 

8.      =1 

9.      =1

10.       =1

11.      =1  

y=_{4  3    1} +     +       +      +    +

+ +       +     +     +      +                      +        (1)

Полученная форма функции называется совершенной дизъюнктивной нормальной формой (СДНФ), так как каждое слагаемое представляет собой конъюнкцию всех аргументов прямом или инверсном виде.

Структурная схема устройства до минимизации показана на рис. 1 в приложении.

Применим карту Карно для минимизации данной функции:

Составим выражение согласно карте Карно

y=  _{4  3    1} ++  ₁ +       (2)

Выражение (2) представляет собой дизъюнктивную нормальную форму (ДНФ).

Применив теорему Де Моргана можно реализовать булевые функции (1) и (2) на базисе И-НЕ:

y= *

*

(3)

y=     (4)

Количество логических элементов после минимизации значительно сократилось. Подсчитаем коэффициент сложности К_с приведенных схем:

для схемы до минимизации: К_с=32+11=43;

для схемы после минимизации К_с =11+4=15.

Реализация функции по СДНФ потребует 5 корпусов ИС (  ), а по минимальной форме 1.3625 (  ). Таким образом минимизация дала нам выигрыш более чем в 3 раз.

С целью получения сравнительно высокого быстродействия и низкого значения потребляемой мощности, для реализации схемы на рис.2 выберем ИС  SN74S10N, которая представляет из себя микросхему серии ТТЛШ, которые позволяют повысить быстродействие за счет применения эффекта Шоттки. Эта ИС при токе потребления 27 мА позволяет получить быстродействие 4,5 нс. Микросхема состоит из трех элементов 3И-НЕ, поэтому для реализации схемы необходимо применить три микросхемы. Окончательны вариант схемы приведен в приложении на рис.2.

Преобразователь двоичного кода в двоично-десятичный

В этой части задания необходимо произвести расчет делителя на 22 Необходимо преобразовать двоичные числа в двоично-десятичные. Цифра 22 не преобразуется, так как  . Таблица истинности делителя приведена в таблице 2.

 Таблица 2

составим функцию и проведем ее минимизацию  для каждого