Прочностной расчет деталей гидромашины (материал пластин – сталь Р18, материал корпусных деталей – чугун)

5. Прочностной расчет деталей машин

Используя рекомендации назначаем следующие материалы для изготовления деталей гидромашины:

·  материал пластин – сталь Р18;

·  материал статора – сталь 20Х с цианированием;

·  материал ротора – сталь 20Х с цианированием;

·  материал  распределительных дисков – латунь;

·  материал подшипников скольжения – сплавы на основе бронзы;

·  материал корпусных деталей – чугун.

5.1 Расчет пластины

Введем следующие допущения:

·  пренебрегаем действием силы трения (трение пластины о статорное кольцо) и центробежной силой, вследствие их малости в сравнении с силой давления жидкости;

·  пластина подвергается чистому изгибу;

·  часть пластины находящаяся в пазу ротора не подвергается действию изгибающего момента.

С учетом введенных допущений, можно составить расчетную схему, показанную на рисунке 11.

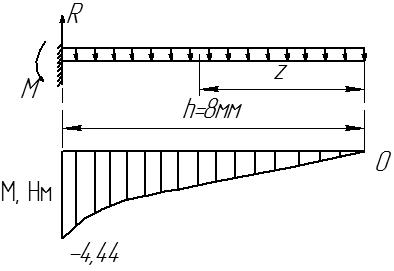
Рисунок 11 – Расчетная схема пластины

Сила действующая на пластину:

Представим силу в виде распределенной нагрузки:

Определим реакцию :

Далее определим момент М:

Далее строим эпюру изгибающего момента (рисунок 12). Изгибающий момент определяем по следующим формулам:

Далее определяем  толщину пластины (), из следующего условия [9, с.301]:

где  момент сопротивления.

Преобразовав получаем:

для легированной стали Р18   Тогда получаем:

Принимаем

Использование стали Р18 оправдывается тем, что значительно уменьшается износ пластин.

Далее рассчитаем радиус закругления кромки пластины. Максимальное напряжение возникаемое в пятне контакта пластины со статором:

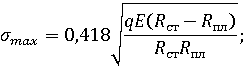
Отсюда получаем выражение для радиуса закругления пластины:

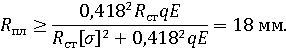
Принимаем 

5.2 Расчет толщины  статорного кольца

Вводя допущения, что жидкость оказывает равномерное давление на всю внутреннею поверхность статора, воспользуемся методикой расчета толстостенных оболочек. Воспользуемся формулой, которая выражает зависимость между внутренним и внешним радиусом статора [9,  c.661, (20.26)]:

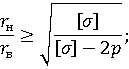
тогда наружный радиус равен:

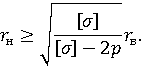
 для стали 20Х;  

Принимаем

5.3 Расчет вала

Определим  диаметр вала насоса:

Требуемый диаметр  выходного конца  вала  определим при расчёте на  чистое  кручение  по допустимым  напряжениям: [] =

Принимаем  []=20∙10⁶ Па

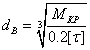
Момент на валу определяется по формуле:

,    принимаем  равным 0,9.

Тогда     

Следовательно   

Принимаем диаметр вала равным 30мм:

Считаем , что на вал насажена шестерня, создающая реактивную силу F_r и окружную F_t,  принимаем диаметр начальной окружности d =28 мм  угол  зацепления .

Вал  передает  момент  М_кр= 50,16Нм

Неуравновешенная  составляющая  силы, передаваемой  муфтой:

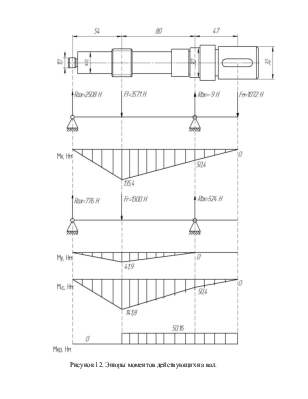
Опорные реакции в вертикальной плоскости:

;   ;  

;     ;   

Проверка: 776 – 1300 +524 = 0;

Строим эпюру изгибающих моментов в вертикальной плоскости (рисунок 12)

Опорные  реакции  в  горизонтальной  плоскости :

Проверка  2508 – 3571 –9+1072 = 0;

Строим эпюру изгибающих моментов в горизонтальной плоскости (рисунок 12)

Находим  опасное сечение, вычислив суммарный изгибающий и момент крутящий. Опасным сечением является сечение 2.

Из условия на прочность . Определим необходимый диаметр вала в опасном сечении

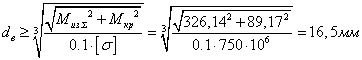; принимаем  d =25 мм

Данный  диаметр  вала  обеспечивает  безотказную  работу  насоса ,  так  как  выдерживает  необходимые  нагрузки.

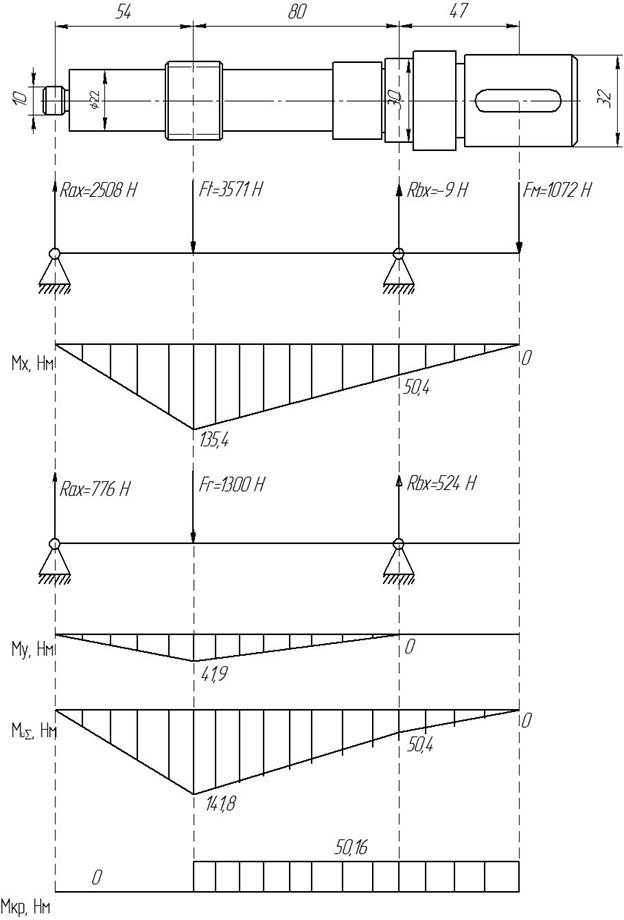
Рисунок 12. Эпюры моментов действующих на вал.

5.4 Выбор подшипников

Расчет проводим по радиальной нагрузке P

P=V∙F_R;

V=1-при вращении внутреннего кольца по отношению n направления нагрузки.

L₁₀=10^-6∙60∙n∙L_k

L₁₀-требуемая долговечность;

L_k-требуемый срок службы подшипника, принимаем  L_k=40000  часов

L₁₀=10^-6∙60∙1500∙40000=3600

Расчет подшипников опоры А:

P_r=1∙223.8=223.8H

-требуемая динамическая грузоподъемность

Принимаем подшипник 301

Расчет подшипников опоры Б:

=668.4

Принимаем подшипник 304, обеспечивающий нормальную работу насоса .

Принятые подшипники, обеспечивают нормальную работу насоса свыше 40000 часов