Константы фазового равновесия определяем по уравнению для идеальных растворов:
![]() .
.
Давления насыщенных паров компонентов определяем по формуле Ашворта:
 , где
, где ![]() .
.
Давление
в колонне переведем в атмосферы: ![]() атм.
атм.
В качестве первого приближения выберем температуру 120оС.
Для
фракции 130 – 140 (![]() оС):
оС):
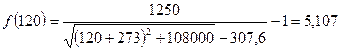 ,
,
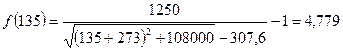 .
.
ДНП
при 120оС ![]() .
.
Константа
фазового равновесия: ![]() .
.
Величина
![]() .
.
Температура
второго приближения: ![]() оС.
оС.
Величина
![]() и
т.д.
и
т.д.
С
помощью 12 итераций определяем, что температура сырья ![]() оС.
оС.
При
данной температуре определяем факторы отпарки всех компонентов сырья ![]() по
уравнению:
по
уравнению:
![]() .
.
Для фракции 130 – 140оС константа фазового равновесия при температуре питания равна 1,326. Фактор отпарки равен:
![]() .
.
Итерационным решением уравнения (5.13) определим рабочее флегмовое
число, принимая в качестве первого приближения ![]() .
.
Определим фактор отпарки условного компонента на температурной границе деления смеси при температуре питания. По формуле Ашворта:
![]() ,
,
![]() .
.
![]() .
.
Определяем константу фазового равновесия условного компонента на
температурной границе деления смеси (компонента с нормальной температурой
кипения 120оС и коэффициентом распределения между дистиллятом и
остатком ![]() ).
Вычисление производим по уравнению (5.10).
).
Вычисление производим по уравнению (5.10).
![]() ,
,
![]()
![]() .
.
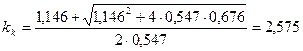 .
.
Эффективную температуру определим из уравнения Ашворта:
![]() ,
,
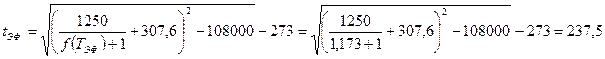 .
.
Определяем константы равновесия всех условных компонентов при эффективной температуре. Например, для фракции 130 – 140оС:
![]() ,
,
![]() .
.
Определяем факторы абсорбции и отпарки всех компонентов при эффективной температуре по уравнениям (5.7) – (5.9) и
![]() .
.
Для фракции 130 – 140оС:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Коэффициенты распределения компонентов определяем по уравнению (5.1):
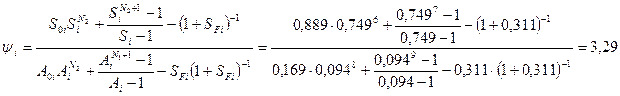 .
.
Примем мольный расход сырья ![]() кмоль/ч.
Тогда мольный расход компонентов определится по формуле:
кмоль/ч.
Тогда мольный расход компонентов определится по формуле:
![]() .
.
Для
фракции 130 – 140 оС ![]() кмоль/ч.
кмоль/ч.
Определяем относительную ошибку вычисления выхода дистиллята:
![]() .
.
![]() .
.
Расход
дистиллята таким образом: ![]() кмоль/ч.
кмоль/ч.
Расход
остатка: ![]() кмоль/ч.
кмоль/ч.
Покомпонентый расход дистиллята и остатка:
![]() ,
,
![]() .
.
Состав дистиллята и остатка:
![]() ,
,
![]() .
.
Результаты расчетов материального баланса колонны отбензинивания приведены в таблице 5.1.2.
|
Фрак-ции, оС |
Моль-ная масса |
SFi |
kiпри tЭФ |
A0i |
S0i |
Ai |
Si |
ψi |
α=Σdi |
α=Σbi |
|||||||
|
xFi, мол. доли |
fi, кмоль/ч |
α=Σfi |
di, кмоль/ч |
yDi, мол. доли |
bi, кмоль/ч |
xWi, мол. доли |
|||||||||||
|
До 28 |
37 |
0,019 |
0,018 |
0,018 |
3,514 |
30,13 |
0,027 |
5,564 |
0,015 |
4,761 |
3,406х х105 |
0,018 |
3,984х х10-4 |
3,984х х10-4 |
5,139х х10-8 |
9,165х х10-10 |
9,165х х10-10 |
|
28–60 |
84,87 |
0,034 |
6,08 |
6,098 |
2,074 |
20,149 |
0,04 |
3,781 |
0,022 |
3,184 |
1,568х х104 |
6,079 |
0,138 |
0,139 |
3,878х х10-4 |
6,917х х10-6 |
6,918х х10-6 |
|
60–80 |
94,19 |
0,036 |
6,068 |
12,165 |
1,263 |
13,803 |
0,058 |
2,59 |
0,032 |
2,181 |
1,002х х103 |
6,062 |
0,138 |
0,277 |
6,051х х10-3 |
1,079х х10-4 |
1,148х х10-4 |
|
80–90 |
100,37 |
0,02 |
3,264 |
15,429 |
0,933 |
10,957 |
0,073 |
2,056 |
0,041 |
1,731 |
209,496 |
3,248 |
0,074 |
0,351 |
0,016 |
2,765х х10-4 |
3,914х х10-4 |
|
90–100 |
104,81 |
0,02 |
3,097 |
18,526 |
0,758 |
9,345 |
0,086 |
1,754 |
0,048 |
1,477 |
76,942 |
3,057 |
0,07 |
0,42 |
0,04 |
7,087х х10-4 |
1,1х х10-3 |
|
100-110 |
109,51 |
0,034 |
5,1 |
23,626 |
0,612 |
7,937 |
0,101 |
1,489 |
0,056 |
1,254 |
30,064 |
4,936 |
0,112 |
0,533 |
0,164 |
2,928х х10-3 |
4,029х х10-3 |
|
110-120 |
114,46 |
0,032 |
4,72 |
28,346 |
0,491 |
6,713 |
0,119 |
1,26 |
0,066 |
1,061 |
12,853 |
4,379 |
0,1 |
0,632 |
0,341 |
6,077х х10-3 |
0,01 |
|
120-130 |
119,68 |
0,021 |
2,921 |
31,267 |
0,392 |
5,653 |
0,142 |
1,061 |
0,079 |
0,893 |
6,14 |
2,512 |
0,057 |
0,689 |
0,409 |
7,296х х10-3 |
0,017 |
|
130-140 |
125,12 |
0,027 |
3,664 |
34,932 |
0,311 |
4,739 |
0,169 |
0,889 |
0,094 |
0,749 |
3,29 |
2,81 |
0,064 |
0,753 |
0,854 |
0,015 |
0,033 |
|
140-150 |
130,75 |
0,038 |
4,964 |
39,895 |
0,246 |
3,956 |
0,202 |
0,742 |
0,112 |
0,625 |
1,947 |
3,279 |
0,075 |
0,828 |
1,685 |
0,03 |
0,063 |
|
150-170 |
139,48 |
0,056 |
6,907 |
46,802 |
0,17 |
2,992 |
0,267 |
0,561 |
0,149 |
0,473 |
1,009 |
3,469 |
0,079 |
0,907 |
3,438 |
0,061 |
0,124 |
|
170-190 |
151,4 |
0,059 |
6,807 |
53,609 |
0,102 |
2,029 |
0,394 |
0,381 |
0,219 |
0,321 |
0,475 |
2,193 |
0,05 |
0,957 |
4,614 |
0,082 |
0,206 |
|
190-220 |
166,79 |
0,09 |
9,671 |
63,28 |
0,052 |
1,215 |
0,658 |
0,228 |
0,366 |
0,192 |
0,188 |
1,531 |
0,035 |
0,992 |
8,139 |
0,145 |
0,351 |
|
220-250 |
187,33 |
0,095 |
9,191 |
72,471 |
0,022 |
0,631 |
1,269 |
0,118 |
0,705 |
0,1 |
0,04 |
0,354 |
8,066х х10-3 |
~1 |
8,837 |
0,158 |
0,509 |
|
250-280 |
211,83 |
0,084 |
7,326 |
79,797 |
8,787х х10-3 |
0,312 |
2,565 |
0,059 |
1,425 |
0,049 |
6,158х х10-4 |
4,509х х10-3 |
1,026х х10-4 |
~1 |
7,321 |
0,131 |
0,64 |
|
280-310 |
240 |
0,071 |
5,587 |
85,384 |
3,265х х10-3 |
0,147 |
5,46 |
0,027 |
3,033 |
0,023 |
5,414х х10-7 |
3,025х х10-6 |
6,884х х10-8 |
~1 |
5,587 |
0,1 |
0,739 |
|
310-340 |
270,48 |
0,075 |
5,265 |
90,649 |
1,128х х10-3 |
0,065 |
12,283 |
0,012 |
6,824 |
0,01 |
1,822х х10-10 |
9,594х х10-10 |
2,184х х10-11 |
~1 |
5,265 |
0,094 |
0,833 |
|
340-370 |
302,98 |
0,035 |
2,241 |
92,89 |
3,6х х10-4 |
0,027 |
29,351 |
5,115х х10-3 |
16,306 |
4,307х х10-3 |
3,082х х10-14 |
6,907х х10-14 |
1,572х х10-15 |
~1 |
2,241 |
0,04 |
0,873 |
|
370-400 |
337,52 |
0,038 |
2,2 |
95,09 |
1,054х х10-4 |
0,011 |
74,918 |
2,004х х10-3 |
41,621 |
1,687х х10-3 |
2,625х х10-18 |
5,777х х10-18 |
1,315х х10-19 |
~1 |
2,2 |
0,039 |
0,912 |
|
400-430 |
374,09 |
0,038 |
2,05 |
97,141 |
2,807х х10-5 |
3,891х х10-3 |
205,583 |
7,302х х10-4 |
114,213 |
6,149х х10-4 |
1,075х х10-22 |
2,205х х10-22 |
5,019х х10-24 |
~1 |
2,05 |
0,037 |
0,949 |
|
430-460 |
412,69 |
0,039 |
1,997 |
99,138 |
6,731х х10-6 |
1,309х х10-3 |
611,102 |
2,457х х10-4 |
339,501 |
2,068х х10-4 |
1,977х х10-27 |
3,949х х10-27 |
8,989х х10-29 |
~1 |
1,997 |
0,036 |
0,985 |
|
460-490 |
453,328 |
0,042 |
0,862 |
100 |
1,437х х10-3 |
4,03х х10-4 |
1,985х х103 |
7,562х х10-5 |
1,103х х103 |
6,368х х10-5 |
1,498х х10-32 |
1,292х х10-32 |
2,94х х10-34 |
~1 |
0,862 |
0,015 |
1 |
Изменение относительной ошибки вычисления выхода дистиллята при
разных флегмовых числах можно наблюдать на графике ![]() .
.
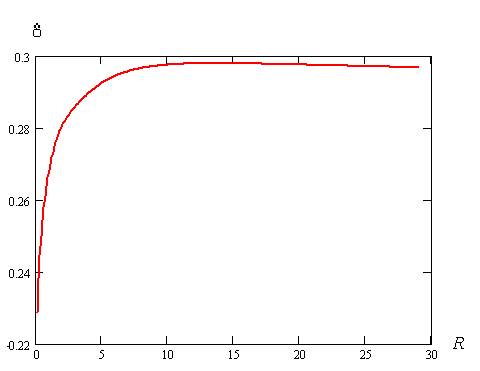
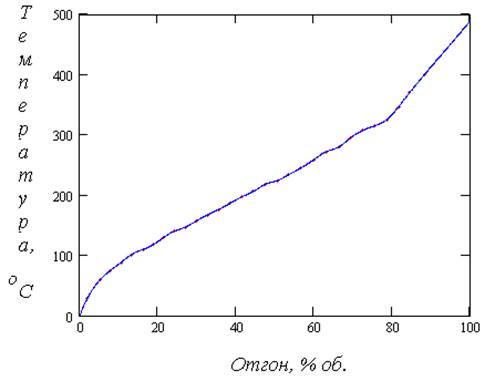
Рис. 5.1.1. ИТК Некрасовской нефти (в % об.).
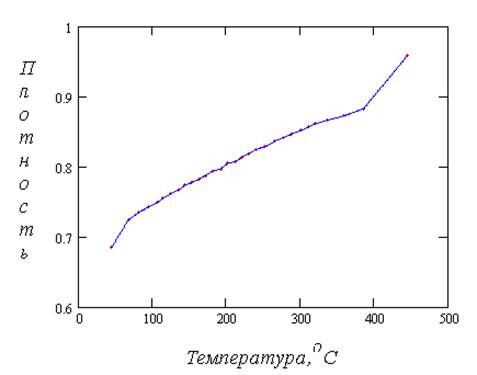
Рис. 5.1.2. Зависимость плотности от средней температуры кипения.
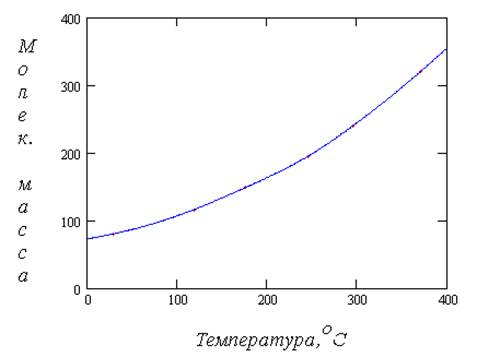
Рис. 5.1.3. Зависимость молекулярной массы от средней температуры кипения
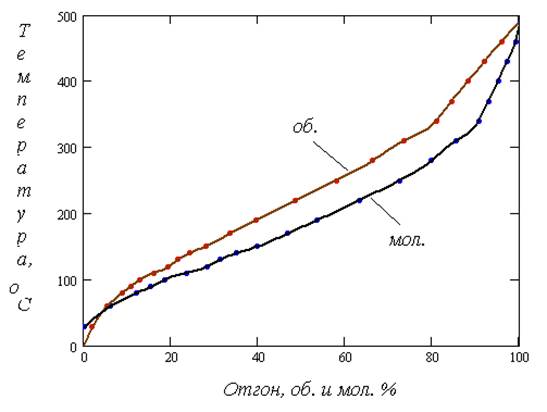
Рис. 5.1.4. ИТК Некрасовской нефти (об. и мол. %).
_________________________________________________________________________
Расчет методом температурной границы. Основные уравнения этого метода записываются по аналогии с уравнением Фенске, в соответствии с которым в режиме бесконечного орошения существует следующая зависимость между числом теоретических тарелок и содержанием в дистилляте и остатке двух компонентов:
![]() ,
(5.16)
,
(5.16)
где
![]() .
.
Если в качестве j-того компонента принять реальный или
условный равнораспределенный между дистиллятом и остатком компонент, для
которого ![]() ,
то нормальная температура кипения этого компонента будет соответствовать
температурной границе деления исходной смеси. При этом уравнение (5.16)
запишется следующим образом:
,
то нормальная температура кипения этого компонента будет соответствовать
температурной границе деления исходной смеси. При этом уравнение (5.16)
запишется следующим образом:
![]() .
(5.17)
.
(5.17)
В режиме с конечным орошением для компонентов, расположенных вблизи температурной границы деления смеси, уравнение (5.17) выполняется в виде аналогичной зависимости
![]() ,
(5.18)
,
(5.18)
где n – индекс фракционирования, принимающий различные значения для компонентов, расположенных слева и справа от температурной границы деления смеси.
Рассмотрим порядок и особенности выполнения проектного расчета процесса ректификации многокомпонентных или непрерывных смесей при заданном разделении двух компонентов в дистиллят или остаток одновременно или порознь.
Используем четыре
степени свободы проектирования процесса ректификации в полной колонне; в
качестве исходных данных выбираем величины ![]() ,
,
![]() (извлечения
компонентов в дистиллят и остаток), β, положение тарелки питания
(извлечения
компонентов в дистиллят и остаток), β, положение тарелки питания ![]() ,
а также состав сырья, его температуру и давление в колонне. В результате
расчета должны быть найдены выход дистиллята е, флегмовое число R, потребное число тарелок N и полные
составы продуктов
,
а также состав сырья, его температуру и давление в колонне. В результате
расчета должны быть найдены выход дистиллята е, флегмовое число R, потребное число тарелок N и полные
составы продуктов ![]() и
и
![]() .
.
В такой постановке задачи расчет ректификации многокомпонентных смесей полностью идентичен расчету ректификации бинарных смесей.
При расчете ректификации
непрерывных смесей в качестве условных компонентов с заданным разделением в дистиллят
и остаток могут быть приняты наиболее легкокипящий и высококипящий компоненты,
которые являются практически нераспределяемыми; это соответственно компоненты в
точках С и А на кривой ИТК (рис. 5.1). Процент
отгона этих компонентов из исходной смеси может быть вычислен в зависимости от
заданных, условий разделения: температурной границы деления смеси по кривой ИТК (![]() )
и налегания температур (
)
и налегания температур (![]() )
конца и начала кипения соседних фракций:
)
конца и начала кипения соседних фракций:
![]() ,
,
![]() , где
, где ![]() -
угол наклона кривой ИТК сырья, оС/% отгона;
-
угол наклона кривой ИТК сырья, оС/% отгона;
![]() -
отбор дистиллята, соответствующий температурной границе деления смеси по кривой
ИТК.
-
отбор дистиллята, соответствующий температурной границе деления смеси по кривой
ИТК.
Извлечение легкокипящего и высококипящего компонентов соответственно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.