Полученные таким образом усилия в сечениях балки соответствуют упругой работе материала. При эксплуатации железобетонных конструкций помимо упругих могут развиться и пластические неупругие деформации. В изгибаемых элементах по мере увеличения внешней нагрузки в растянутых зонах в бетоне появляются трещины, нарушается сцепление, напряжения растянутой арматуры достигают предела текучести, образуется пластический шарнир. Текучесть арматуры сопровождается нарастанием прогибов элемента и взаимным поворотом сечений. При этом момент, воспринимаемый пластическим шарниром остается постоянным. При дальнейшем увеличении нагрузки в статически неопределимых системах происходит перераспределение усилий на другие сечения, при этом соблюдается правило – сумма пролетного и полусумма опорных изгибающих моментов равна моменту в балке, свободно лежащей на двух опорах («балочный момент»). При расчете неразрезных балок появляется возможность корректировать «упругую» эпюру изгибающих моментов, выравнивая их опорные и пролетные значения. Для ограничения раскрытия трещин нормы рекомендуют перераспределять моменты так, чтобы выровненный момент отличался от момента в упругой стадии не более чем на 30 %.
Надежная работа сечений обеспечивается также более жестким ограничением высоты сжатой зоны:
ξ ≤ ξR = 0,37
Перераспределение изгибающих моментов позволяет уменьшить высоту балок, экономить до 20…30% стали.
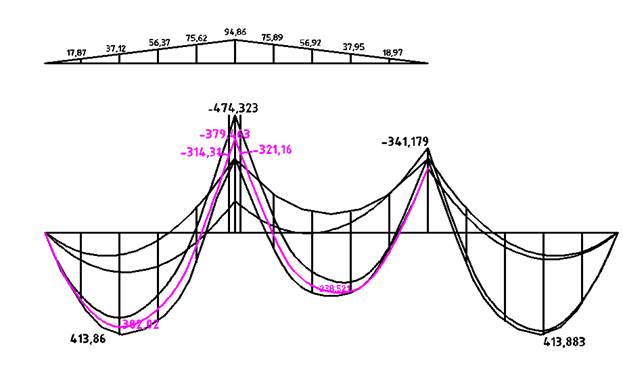
Рисунок 8. Перераспределение изгибающих моментов
После уменьшения моментов строим огибающие эпюры.
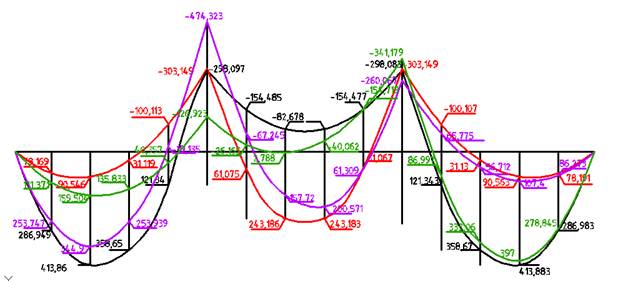
Рисунок 9. Эпюры моментов от сочетания нагрузок
После уменьшения моментов строим огибающие эпюры.
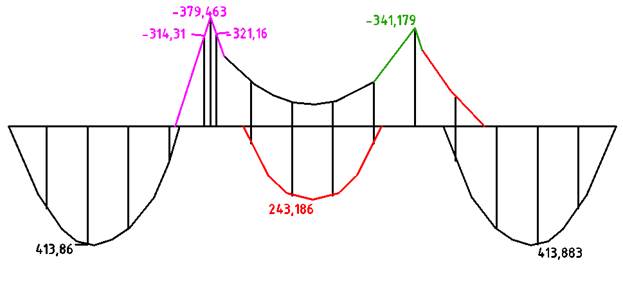
Рисунок 10. Огибающая эпюра моментов
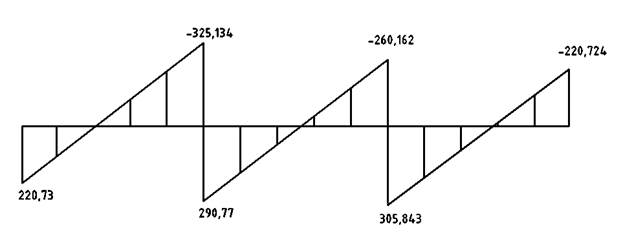
Рисунок 11. Огибающая эпюра поперечных сил
Расчет главной балки по нормальным сечениям
1. Опора
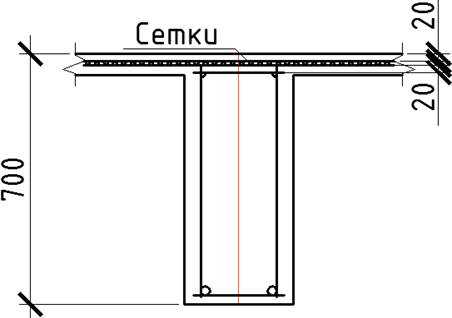
Рисунок 12. Сечение главной балки к расчету армирования на опоре
класс бетона B 20 – Rb = 11,5 МПа
γb1 * Rb = 0,9 * 11,5 = 10,35 МПа арматура класса А 400 – Rs = 350 Мпа
Mоп = 321,16 кН * м
1. h0 = h – a= 700 –80= 620мм – рабочая высота сечения
2. αm =
=
=
0,269
3.ξ = 1 - √1 – 2 * αm = 1 - √1 – 2 * 0,269 = 0,32 – относительная высота сжатой зоны
Для сечений, в которых предусмотрено образование пластического шарнира должно выполняться условие:
ξ < ξR = 0,37
ξ = 0,32 < ξR = 0,37 – условие выполняется
4.
η = 1 - 
=
1
- 
=
0,84
5. As
= 
=
=
1761,9 мм2 – требуемая площадь сечения арматуры
В качестве армирования принимаем стержневую арматуру 4Ø 25,
As = 1963 мм2
a = 20 + 4+ 4+ 4 +20 + 25 + 25/2 = 89,5 мм
h0 = h – a = 700 – 89,5 = 610,5 мм
Проверка несущей способности:
xф
= 
=
=
221,27 мм
Mu
= γb1* Rb * b * xф
* (h0 - 
)
Mu=
10,35 * 103 *0,3 * 0,22127 * (0,6105 - 
)
= 343,43 кН*м
343,43 >321,16 кН*м . Прочность арматуры достаточна.
2. Пролет 1
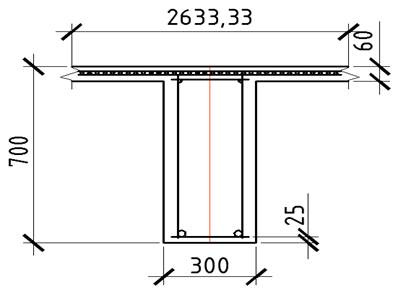
Рисунок 13. Сечение главной балки к расчету армирования в пролете 1
класс бетона B 20 Rb = 11,5 МПа
γb1 * Rb = 0,9 * 11,5 = 10,35 МПа арматура класса А 400 – Rs = 350 МПа
Mпр1 = 413,86 кН * м
1. a = 25 + 25/2 = 37,5 мм
2. h0 = h – a= 700 – 37,5 = 662,5 мм – рабочая высота сечения
3.
γb1
* Rb * bf | * hf | * (h0
- 
)
= 10,35 * 103 * 2,63333 * 0,06 * (0,6625 - 
)
= = 1034,33 кН
Mпр1 = 413,86 кН * м < 1034,33 кН => x в полке
4.
αm
=
=
=
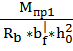0,0346
5. ξ = 1 - √1 – 2 * αm = 1 - √1 – 2 * 0,0346 = 0,0352 – относительная высота сжатой зоны
6.
η = 1 - =
1
- 
=
0,98
7.
As
= 
=
= 1821,27
мм – требуемая площадь сечения арматуры
В качестве армирования принимаем стержневую арматуру 4Ø 25,
As = 1963 мм2 .
a = aз.с. + d + d/2 = 25 + 25 + 25/2 = 62,5 мм
h0 = h – a= 700 – 62,5 = 637,5 мм
Проверка несущей способности:
xф
= 
=
=
25,2 мм
Mu
= γb1*
Rb *
bf |
* xф
* (h0
- )
= 10,35 * 103 * 2,63333 * 0,0252 * (0,6375 -
-
)
= 429,2 кН* м > Mпр1
= 413,86 кН * м, прочность арматуры достаточна.
3. Пролет 2
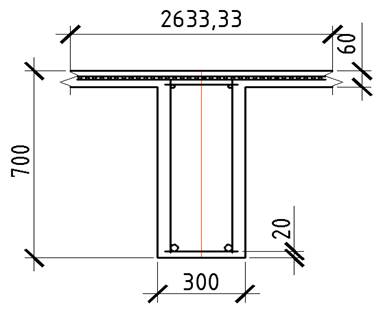
Рисунок 14. Сечение главной балки к расчету армирования в пролете 2
класс бетона B 20 Rb = 11,5 МПа
γb1 * Rb = 0,9 * 11,5 = 10,35 МПа арматура класса А 400 – Rs = 350 МПа
Mпр2 = 243,186 кН * м
1. a = 25 + 25/2 = 37,5 мм
2. h0 = h – a= 700 – 37,5 = 662,5 мм – рабочая высота сечения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.