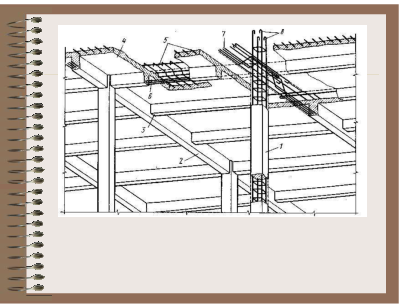
Расчет элементов железобетонных конструкций по II группе предельных состояний

РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО II ГРУППЕ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ

Основные гипотезы расчета по трещинообразованию :

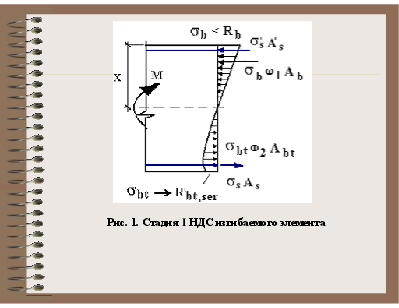
1. Перед образованием трещин напряжения в растянутом бетоне принимаются равными расчетному сопротивлению растяжению по 2 группе предельных состояний, т.е. 2. При расчете по образованию трещин действует принцип суперпозиции – принцип независимости действия сил. 3. Действует гипотеза плоских сечений. 4. Относительную деформацию крайнего растянутого волокна бетона принимают равной ее предельному значению εbt,ult при кратковременном действии нагрузки. 5. Напряжения в арматуре принимают в зависимости от относительных деформаций как для упругого тела.

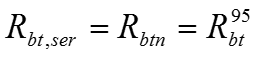
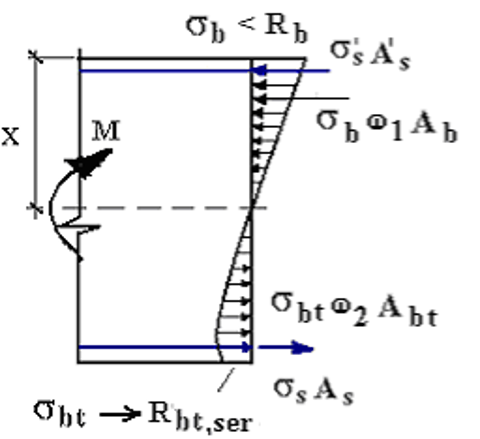
Рис. 1. Стадия I НДС изгибаемого элемента

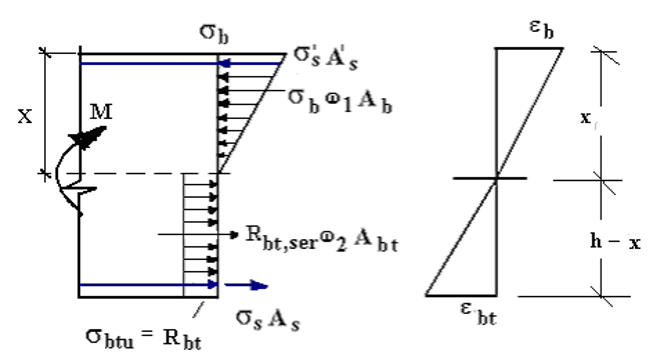
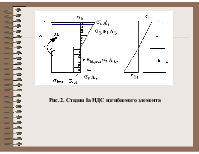
Рис. 2. Стадия Iа НДС изгибаемого элемента

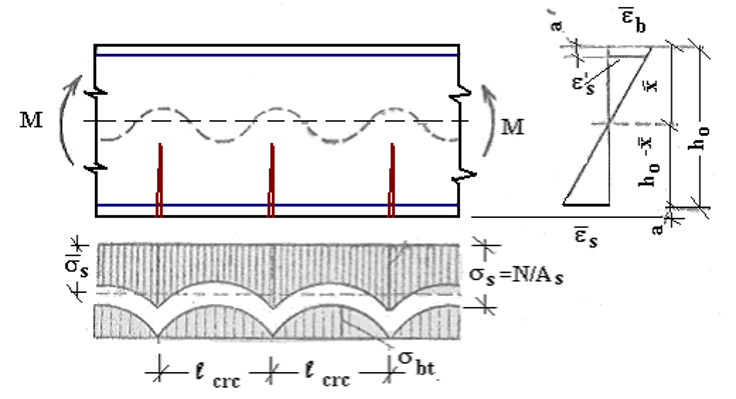
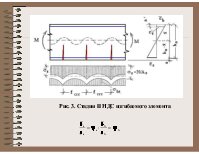
Рис. 3. Стадия II НДС изгибаемого элемента

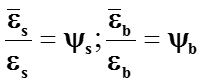
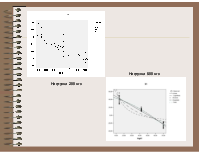
Нагрузка 600 кгс

Нагрузка 200 кгс

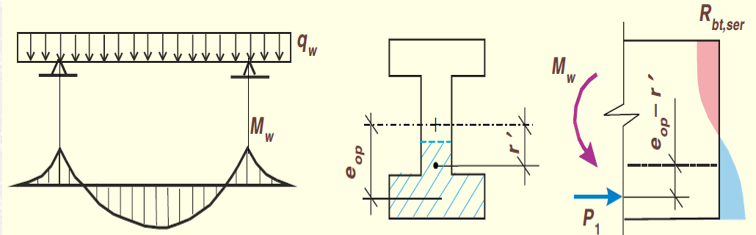
Определение ширины раскрытия трещин Ширина раскрытия трещин, нормальных к продольной оси элемента, представляет собой разность удлинений арматуры и растянутого бетона на участке между трещинами длиной , т.е.

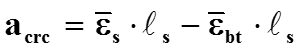
Средней деформацией растянутого бетона как величиной малой в сравнении со средней деформацией растянутой арматуры обычно пренебрегают и принимают

или

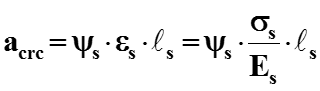
По СП 63.13330.2012 по п.8.2.15 ширину раскрытия трещин, нормальных к продольной оси элемента , определяют:

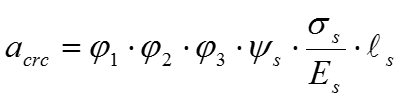
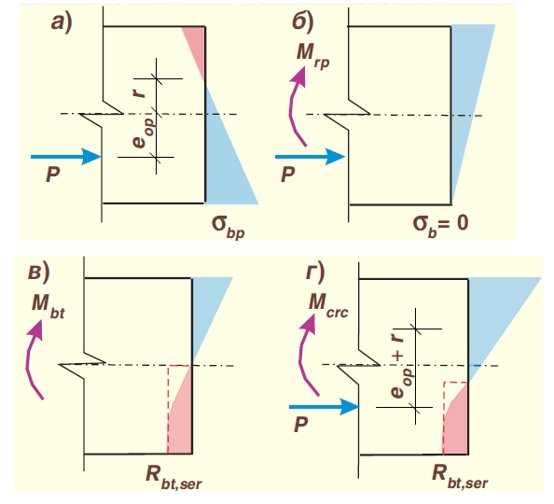
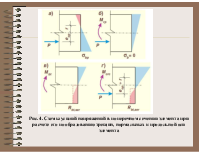
Рис. 4. Схемы усилий напряжений в поперечном сечении элемента при расчете его по образованию трещин, нормальных к продольной оси элемента

В практике проектирования встречаются случаи, когда по расчету Mcrc  Mu. Чаще всего подобное происходит в преднапряженных конструкциях с центральным армированием (сваях, дорожных бортовых камнях и т.п.), которым арматура требуется только на период перевозки и монтажа и у которых она расположена по оси сечения, т.е. вблизи нейтральной оси. Объясняется это явление следующими причинами.

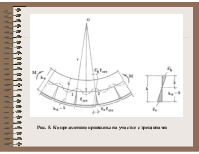
В момент образования трещины растягивающее усилие в бетоне передается арматуре при соблюдении условия: Mcrc= Nbt z1 = Ns z2 (рис. 5) – для простоты рассуждений работа арматуры до образования трещины здесь не учтена.

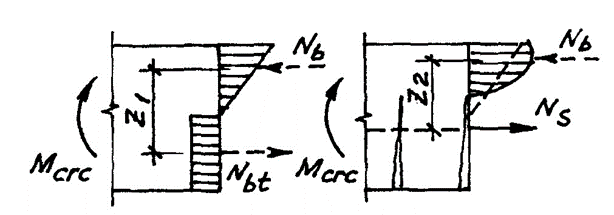
рис. 5

Если окажется, что Ns = Rs As  Nbt z1 / z2, то одновременно с образованием трещин происходит и разрушение элемента, что подтверждается многочисленными экспериментами. Для некоторых конструкций такая ситуация может оказаться чреватой внезапным обрушением, поэтому Свод Правил в этих случаях предписывает увеличить на 15 % площадь сечения арматуры, если она подобрана расчетом по прочности. Напрягаемая арматура может быть и поперечной, т.к. она создает поперечное обжатие, увеличивая напряжения y, которые, в свою очередь, уменьшают напряжения mt и повышают, тем самым, трещиностойкость наклонных сечений.

mt = (x + y)/2 + (x – y)2/4 – 2xy,

х  нормальные напряжения от действия силы обжатия Р и изгибающего момента М от внешней нагрузки;

y  вертикальные напряжения от местного действия опорных реакций и сосредоточенных сил, а также от усилия обжатия преднапряженными хомутами (поперечной арматурой) или отогнутой арматурой; xy  касательные напряжения от действия Q и от усилия обжатия преднапряженной отогнутой арматурой.

Отогнутая арматура, кроме того, уменьшает значения xy, что также благоприятно влияет на трещиностойкость. Без такой арматуры очень трудно обеспечить трещиностойкость наклонных сечений элементов 1-й категории.

Расчет на закрытие трещин У элементов 2-й категории трещиностойкости при действии полной нормативной нагрузки в сечениях возникают усилия (например, при изгибе Мtot), при которых допускается ограниченное по ширине раскрытие трещин. Когда снимается кратковременная нагрузка и остается только постоянная и длительная, то усилия уменьшаются (Мl) и трещины закрываются. Чтобы быть уверенными в их надежном закрытии, нужно обеспечить сжатие растянутой грани напряжениями b от совместного действия усилий Мl и силы обжатия Р2 (с учетом всех потерь и при коэффициенте точности натяжения sp= 1). В Своде Правил минимальное значение b установлено равным