![]()
![]() k
k
 |
T2 t
7 Звено чистого запаздывания.
Д.у. ![]()
ПФ: ![]()
h(t)
![]() 1(t)
1(t)
![]() h(t)=1 (t-
h(t)=1 (t-![]() )
)
 |
g(t)
t
![]()
![]()
![]()
![]()
![]()
![]()
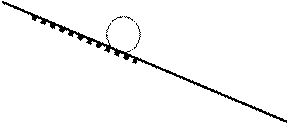
Звено запаздывания осуществляет
операцию сдвига входного сигнала g(t)
на время ![]() “назад”, т.е. выходной сигнал y(t) равен входному, но отодвинутому на
“назад”, т.е. выходной сигнал y(t) равен входному, но отодвинутому на ![]() в прошлое.
в прошлое.
Пример: магнитофон с лентой или магнитным барабаном, транспортер и др.
![]() АФЧХ:
АФЧХ: ![]() y(t),g(t)
y(t),g(t)

 АЧХ:
АЧХ: ![]()
ФЧХ: ![]() g(t)
g(t)
![]() ЛАХ:
ЛАХ: ![]() y(t)=g(t-
y(t)=g(t-![]() )
)
![]()
![]()
![]()
t
0
Последовательное соединение динамических звеньев.
Полагаем звенья однонаправленными и независимыми. Это значит, что подключение к звену следующего звена не изменяет значений выходной входной переменных. Для Эл. цепей это означает бесконечно малое выходное и бесконечно большое входное сопротивления. Сигнал распространяется только в одном направлении – от входа к выходу.
![]()
![]()
![]() g1(p)
g2(p) g3(p) g4(p)
g1(p)
g2(p) g3(p) g4(p)
![]()
![]()
![]()
![]() W1(p) W2(p) W3(p)
W1(p) W2(p) W3(p)
![]() .
.
Очевидно, ![]() , т.е. ПФ-я последовательно
соединенных звеньев равна произведению их ПФ-ций.
, т.е. ПФ-я последовательно
соединенных звеньев равна произведению их ПФ-ций.
Подставим вместо pàjw: ![]() Очевидно, что
АЧХ последовательного соединения:
Очевидно, что
АЧХ последовательного соединения: ![]()
ФЧХ последовательного соединения: ![]()
ЛА ФЧХ последовательного соединения:
![]()
Пример: ![]() . Последовательно
соединенное интегральное звено и форсирующее звено с k=1.
. Последовательно
соединенное интегральное звено и форсирующее звено с k=1.
![]()
![]()
![]()
![]()
![]() g
y
g
y
k/p 1+pT
Строим ЛАХ и ФЧХ каждого из звеньев, а затем геометрически суммируем их.
L(w)
 |
 -1 ∑
-1 ∑![]() (w)
(w)
![]()
![]()
![]()
![]() k/p 1+pT
k/p 1+pT
![]()
![]() w=k
w=k
![]()
![]()
![]() lgw
lgw
1/T
![]()
![]()

![]()

![]() 900
900
1/T lgw
∑![]() (w)
(w)
![]() -900
-900
k/p
Метод построения ЛАХ последовательного соединения.
1) Определяют
сопрягающие частоты ![]() ;
;
2) Слева от
первой сопрягающей частоты проводят прямую с наклоном ![]() , если в ПФ имеется
, если в ПФ имеется ![]() диф. звеньев или с наклоном
+m, если в ПФ имеется m
дифференцирующих звеньев. Эти прямsе пересекают ось
абсцисс в точках:
диф. звеньев или с наклоном
+m, если в ПФ имеется m
дифференцирующих звеньев. Эти прямsе пересекают ось
абсцисс в точках:
- для диф. звена ![]()
![]() - для диф. звена
- для диф. звена ![]()
![]()
![]()
![]()
![]()
![]() 3) На сопрягающих частотах
изменяется наклон асимптотической ЛАХ на
3) На сопрягающих частотах
изменяется наклон асимптотической ЛАХ на ![]() 1
при подключении форсирующего +1 или апериодического -1 звеньев или на
1
при подключении форсирующего +1 или апериодического -1 звеньев или на ![]() 2 для форсирующего +2
или колебательного -2 звена II порядка.
2 для форсирующего +2
или колебательного -2 звена II порядка.
4) Уточняют полученную асимптотическую ЛАХ.
Пример: ![]() , k=200,
w2=1, w1=0.1,
w3=50.
, k=200,
w2=1, w1=0.1,
w3=50.
![]() Пусть T1>T2>T3 à w1<w2<w3 (wi=Ti-1). Начинаем с построения ЛАХ диф.
звена. Из (+) w=k проводим
-1 . Определяем и откладываем w1,w2,w3. Начальный
участок ФЧХ определяется количествам диф. звеньев. Затем проявляется аТ звено,
потом перегиб за счет форсирующего и, наконец, последнее аТ звено.
Пусть T1>T2>T3 à w1<w2<w3 (wi=Ti-1). Начинаем с построения ЛАХ диф.
звена. Из (+) w=k проводим
-1 . Определяем и откладываем w1,w2,w3. Начальный
участок ФЧХ определяется количествам диф. звеньев. Затем проявляется аТ звено,
потом перегиб за счет форсирующего и, наконец, последнее аТ звено.
![]()

![]() L
L
-1
 |
![]()
![]() -2
-2
 -1
-1
![]() w1 w2
20 w=k=20 w
w1 w2
20 w=k=20 w
![]() 0.1 1 w3=50
0.1 1 w3=50
 |
-2
![]()
![]()

![]() 900
900
450 ![]() 2
2


![]() w
w
![]()
![]() -450 -450
-450 -450
![]() 1
1
 |
∑![]() (w)
(w)
-1800
Определение значения АЧХ на некоторой частоте wх по передаточной функции.
Значение W(wx) не зависит от последующих звеньев, сопрягающие частоты которых больше wx.
ПРАВИЛО: 1. В W(p) вместо р подставляют wx ; W(p) à W(wx).
2. Отбрасывают в W(wx) звенья, сопрягающая частота которых расположена за wx (справа).
3. В оставшихся звеньях W(wx) отбрасывают единицу
(н/ч асимптоту), а в звеньях II порядка отбрасывают и
члены вида ![]() (W(w)=k/(wT)2).
(W(w)=k/(wT)2).
Пример: ![]()
![]() раза, (12дБ).
раза, (12дБ).
Определение частоты среза по W(p).
Из ЛАХ находим приближенное значение wc. Если неизвестно, где wc, прибегают к методу проб.
W(w)>1 при w<wc; W(w)<1 при w>wc.
ПРАВИЛО: 1. В W(p) вместо р поставляем wc.
2. Отбрасываем звенья с сопрягающей частотой больше wc.
3. В оставшихся звеньях
отбрасывают 1 и ![]() .
.
4. В левой части уравнения вместо W(w) записывают 1 и решают уравнение относительно wc.
Пример: ![]() -
из ЛАХ.
-
из ЛАХ.
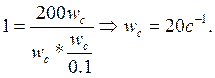
Определение фазы на заданной частоте.
При наличии калькулятора – прямой
расчет: ![]()
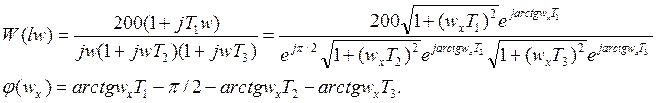
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.