Трехкомнатный двухквартирный жилой дом (Расчетно-конструктивный раздел дипломного проекта)

2. РАСЧЕТНО – КОНСТРУКТИВНЫЙ РАЗДЕЛ

2.1 Расчет стропильной ноги

Конструкция выполнена из ели – 1-го сорта;

Тепловлажностный режим эксплуатации – А- ΙΙ;

Класс ответственности здания — П. γn = 0,95;

Угол наклона кровли к горизонту — α = 41°.

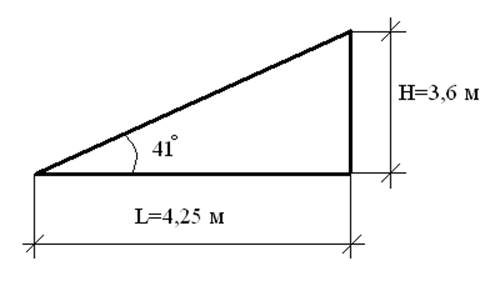
tg α = 3,6/4,25 = 0,85 = 41°

cos α = 41°= 0,75; sin α = 41°= 0,66

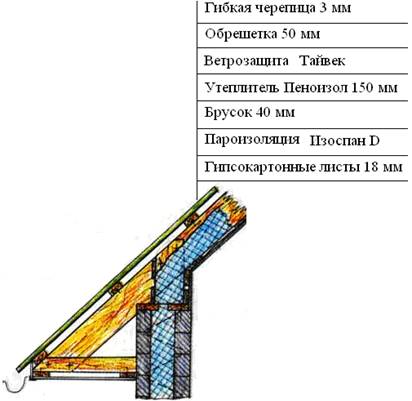
2.1.1 Нагрузка на 1 м² покрытия

Таблица 2.1

Нормативная нагрузка	Подсчет нагрузки	Норма-тивная нагруз-ка, кПа	γf	Расчетная нагрузка, кПа
Ι. Постоянная: 1. Гибкая черепица и  обрешетка 2. Ветрозащита 3. Утеплитель 4. Брусок 5. Пароизоляция 6. ГКЛ	δ•γ=0,15м•0,15 кН/м³ δ•γ=0,04м*5кН/м³ δ•γ=0,018м*8кН/м³	gnтаб1= 0,054 - 0,023 0,2 - 0,144	1,2 1,1 1,1	gтаб1= 0,062 - 0,028 0,22 - 0,158
Итого постоянная:		gn =0,421		g =0,468
—Sg =3,2 кПа —П снеговой район	Sg•μ•cosα= 3,2кПа•0,54•0,75	Sn =1,296	1,3	S=1,685
		qn =1,717		q=2,153

 

Собственный вес стропильной ноги принимаем ориентировочно в размере 5% веса всего покрытия, включая снег (К = 1,05)

2.1.2 Нагрузка на 1 м стропильной ноги, включая ее собственный вес — расчетная: q (кН/м) = q (кПа)• l2 (м)•К•γn•cosα, где l2 – шаг стропильных ног (м);

q =2,153•0,8•1,05•0,95•0,75=1,289 кН/м

2.1.3 Стропильную ногу рассчитываем как однопролетную наклонную балку по наибольшему пролету между опорами (опорами считаются: мауэрлат, прогон; ригель не является опорой)

Наибольший пролет — l₃= 5,09 м

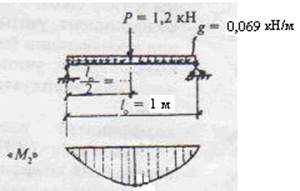
Стропильную ногу рассчитываем на поперечный изгиб на нагрузки от собственного веса кровли и снега (q) и веса человека с инструментом Р=1,2кН.

Расчетная схема

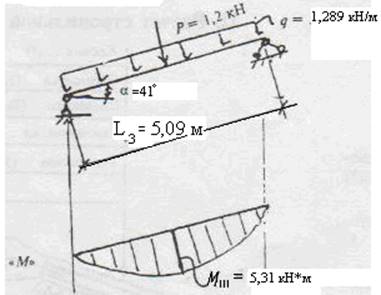
2.1.4 Определяем изгибающий момент:

МΙΙΙ= q•l²3/8+ Р•l3•cosα/4;

МΙΙΙ= 1,289•5,09²/8+1,2•4,25•0,75/4=5,31 кН•м =531 кН•см;

2.1.5 Расчетное сопротивление древесины стропильной ноги:

Ru = Ru таб•mт•mв•mб•mп , где Ru — расчетное сопротивление древесины изгибу;

mв — коэффициент, учитывающий условия эксплуатации;

 

mт — коэффициент, учитывающий температуру эксплуатации;

mб — коэффициент условий работы;

mп — коэффициент, учитывающий породу древесины;

Ru = 14•1•1•1•0,8 = 11,2 МПа=1,12 кН/см²

2.1.6 Требуемый момент сопротивления:

Wтр = МΙΙΙ / Ru = 531/1,12 = 474,1 см³;

По сортаменту досок принимаем сечение b×h = 100×180 мм;

Wx = b•h²/6 = 10•18²/6 = 540 см³;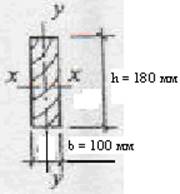                    

Ix = b•h³/12 = 10•18³/12 = 4860 см⁴;

2.1.7 Определение прогиба стропильной ноги

f = (5•qn • l⁴3)/(384•Е•Ix)+ (Рn • l³3 •cosα)/(48•Е•Ix), где qn – нормативная нагрузка на 1 м стропильной ноги, включая ее собственный вес

qn (кН/м) = q n (кПа)• l2 (м)•γn•cosα + b•h•ρ0;

qn (кН/м) = 1,717•0,8•0,95•0,75+0,1•0,18•6= 1,09 кН/м;

Е=10кН/м²;

Рn =1 кН;

f=(5•1,09•5,09⁴)/(384•10•281•10)+(1•5,09³•0,75)/(48•10•281•10)= 0,04 м;

Относительный прогиб стропильной ноги

f/l3 = 0,04/5,09 = 0,008 ≤ l3/n0 =5,09/200 = 0,025

Вывод: жесткость стропильной ноги достаточна.

 

2.2 Расчет балки перекрытия

2.2.1 Нагрузка на 1 м² перекрытия

Таблица 2.2

Нормативная нагрузка	Подсчет нагрузки	Норма-тивная нагруз-ка, кПа	γf	Расчетная нагрузка, кПа
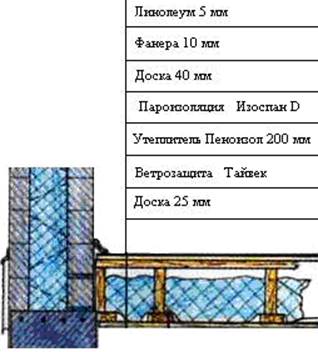
Ι. Постоянная: 1. Линолеум 2. Фанера 3. Доска 40 мм 4. Пароизоляция 5.Утеплитель Пеноизол 6. Ветрозащита 7 .Доска 25 мм	δ•γ=0,005м•18 кН/м³ δ•γ=0,01м•6кН/м³ δ•γ=0,04м•5кН/м³ δ•γ=0,2м•0,15кН/м³ δ•γ=0,025м•5кН/м³	0,09 0,06 0,2 0,03 0,125	1,1 1,1 1,1 1,2 1,1	0,099 0,066 0,22 0,036 0,138
Итого постоянная:		gn =0,505		g =0,559
— р = 1,5 кН/м²(т. 3, стр. 5 СНиП 2.01.07-85 «Нагрузки и воздействия»)	р•l2, где l2 – расстояние между балок, 1,5кПа•0,8м	рn =1,5	1,3	р=1,95
		qn =2,005		q=2,509

 

Собственный вес балки перекрытия принимаем ориентировочно в размере 5% веса всего перекрытия, включая нагрузку (К = 1,05);

2.2.2 Нагрузка на 1 м балки перекрытия, включая ее собственный вес — расчетная: q (кН/м) = q (кПа)• l2 (м)•К,

l2 – шаг балок перекрытий;

q =2,509•0,8•1,05 = 2,11 кН/м

2.2.3 Балку перекрытия рассчитываем как однопролетную балку по наибольшему пролету между опорами.

Наибольший пролет — l₃= 5,3 м

Балку перекрытия рассчитываем на поперечный изгиб на нагрузки от собственного веса и временной нагрузки

Расчетная схема

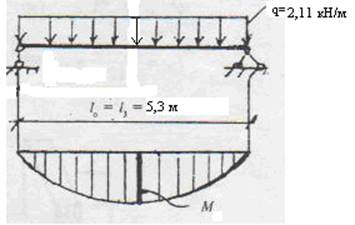
2.2.4 Определяем изгибающий момент:

М= q•l²3/8;

М= 2,11•5,3²/8=7,41 кН•м = 741 кН•см;

2.2.5 Расчетное сопротивление древесины балки перекрытия:

Ru = Ru таб•mт•mв•mб•mп , где Ru — расчетное сопротивление древесины изгибу;

mв — коэффициент, учитывающий условия эксплуатации;

mт — коэффициент, учитывающий температуру эксплуатации;

mб — коэффициент условий работы;

mп — коэффициент, учитывающий породу древесины;

Ru = 14•1•1•1•0,8 = 11,2 МПа=1,12 кН/см²;

2.2.6 Требуемый момент сопротивления:

Wx = М / R = 741/1,12 = 661,6 см³

По сортаменту досок принимаем сечение b×h = 100×220 мм;

Wx = b•h²/6 = 10•22²/6 = 806,7 см³                     

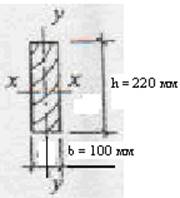
Ix = b•h³/12 = 10•22³/12 = 8873,3 см⁴

2.2.7 Определение прогиба балки перекрытия:

f = (5•qn • l⁴)/(384•Е•Ix), где qn – нормативная нагрузка на 1 м балки перекрытия, включая ее собственный вес;

qn (кН/м) = q n (кПа)• l3 (м)+ b•h•ρ0;

qn = 2,005•5,3+0,1•0,22•5 = 10,7 кН/м

Е=10кН/м²

f = (5•10,7•5,3⁴)/(384•10•281•10)= 0,14 м;

Относительный прогиб стропильной ноги

f/l3 =0,14/5,3 =0,026≤ l3/n0 = 5,3/200 = 0,027

Вывод: жесткость балки перекрытия достаточна.

 

2.3 Расчет элементов лестницы

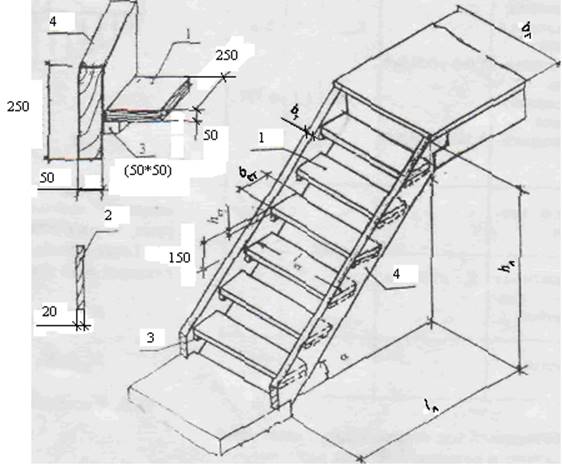
Конструктивные элементы лестницы:

1. Проступь; 2. Подступенок; 3. Брусок; 4. Тетива.

Конструкция выполнена из ели – 1-го сорта;

Тепловлажностный режим эксплуатации – А- ΙΙ;

Класс ответственности здания — П. γn = 0,95;

Угол наклона лестницы — α = 54°.

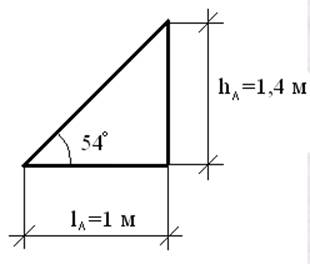      tg α = h л /l л; tg α = 1,4/1 = 1,4 = 54°;

cos α = 54°= 0,59; sin α = 54°= 0,81;

 

2.3.1 Расчет проступи

2.3.1.1 Нагрузка на 1 м  длины проступи

Таблица 2.3

Нормативная нагрузка	Подсчет нагрузки	Норма-тивная нагруз-ка, кН/м	γf	Расчетная нагрузка, кН/м
Ι. Постоянная: 1. Собственный вес проступи	hст•bст•γ=0,05м• •0,25м•5кН/м³	0,063	1,1	0,069
Итого постоянная:		gn =0,063		g =0,069
— р = 1,5 кН/м²(т. 3, стр. 5 СНиП 2.01.07-85 «Нагрузки и воздействия»)	р•bст; 1,5кПа•0,25м	Рn =0,375	1,2	Р=0,45
		qn =0,438		q=0,519

2.3.1.2 Расчет проступи производится по прочности и жесткости при:

а) воздействии собственного веса g и нагрузки на 1 м² лестничного марша Р — 1-й случай;

б) воздействии собственного веса g и сосредоточенной нaгрузки

Рn  = 100 кгс= 1 кН (человек с грузом) — 2-й случай.

Проступь рассматривается как однопролетная балка

2.3.1.3 Определение изгибающих моментов а) для 1-го случая

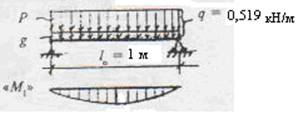
М1 = q•l²0/8; М1 = 0,519•1²/8= 0,065 кН•м;

М1n = qn •l²0/8; М1n = 0,438•1²/8= 0,055 кН•м;

 

б) для 2-го случая

Р = Рn • γf =1кН•1,2 = 1,2 кН

М2 = q•l²0/8+Р• l0 /4; М2 = 0,519•1²/8+1,2•1/4= 0,365 кН•м;

М2n = qn •l²0/8+ Рn• l0 /4; М2n = 0,438•1²/8+1•1/4= 0,305 кН•м;

Наиболее не выгодный случай – 1-й

К расчету принято:

М = Мmax =0,365 кН•м.

Мn = Мn max =0,305 кН•м.

2.3.1.4 Определение геометрических характеристик сечения

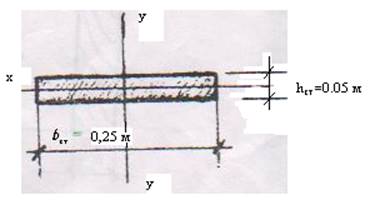
Wx = bст•hст²/6 = 5•25²/6 = 520,83 см³;

Ix = bст•hст³/12 = 5•25³/12 = 6510,42 см⁴;

2.3.1.5 Проверка прочности ступени

σx = Μ/Wx≤ Ru , где Ru = Ru таб•mт•mв•mб•mп , где Ru — расчетное сопротивление древесины изгибу;

mв — коэффициент, учитывающий условия эксплуатации;

mт — коэффициент, учитывающий температуру эксплуатации;

mб — коэффициент условий работы;

 

mп — коэффициент, учитывающий породу древесины;

Ru = 14•1•1•1•0,8 = 11,2 МПа;

σx = 0,365/0,005= 73 кН/м² = 0,73 МПа < Ru = 11,2 МПа.

Вывод: прочность проступи обеспечена.

2.3.1.6 Проверка жесткости проступи

f/l0 = (Мn•l0)/(10•Е•Ix);

f/l0 = (0,305•1)/(10•10•651•10)= 0,00004

f/l0= 0,00004 <1/n0 = 1/200 = 0,005

Вывод: жесткость достаточна.

2.3.2 Расчет тетивы

2.3.2.1 Нагрузка на 1 м длины тетивы

Таблица 2.4

Нормативная нагрузка	Подсчет нагрузки	Норма-тивная нагруз-ка, кН/м	γf	Расчетная нагрузка, кН/м
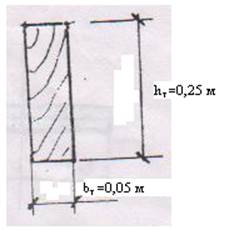
Ι. Постоянная: 1. Собственный вес проступи 2. Собственный вес подступенка 3. Собственный вес бруска 4. от ограждения	hст•lст•γ=0,05м• •0,25м•5кН/м³ bп•(lст/2)•γ=0,15м• •1м/2)•5кН/м³ bб•hб•γ=0,05м• •0,05м•5кН/м³	0,063 0,375 0,013 0,2	1,1 1,1 1,1 1,2	0,069 0,413 0,014 0,24

5. Собственный вес тетивы	bт•hт•γ=0,05м• •0,25м•5кН/м³	0,063	1,1	0,069
Итого постоянная:		gn =0,714		g =0,805
— р = 1,5 кН/м²(т. 3, стр. 5 СНиП 2.01.07-85 «Нагрузки и воздействия»)	р•(bл/2)•cos α; 1,5кПа•(1м/2)•0,59	Рn =0,443	1,2	Р=0,531
		qn =1,157		q=1,336

2.3.2.2 Расчет тетивы производится по прочности и по жесткости

Расчет по прочности производится как для сжато-изогнутого элемента, так как α >30°. Рассматриваем тетиву как однопролетную балку.

2.3.2.3 Определение расчетных усилий

qxn = qn•cosα•γn; qxn = 1,157•0,59•0,95= 0,649 кН/м

qx = q•cosα•γn; qx =1,336•0,59•0,95= 0,749 кН/м

qуn = qn•sinα•γn; qуn =1,157•0,81•0,95= 0,89 кН/м

qу = q•sinα•γn; qу =1,336•0,81•0,95= 1,028 кН/м

Расчетная схема тетивы

 

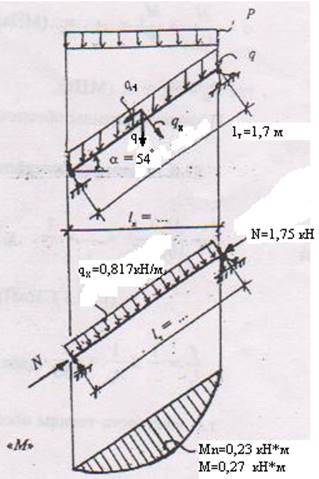
Расчетный пролет тетивы: lл =1 м; lт = lл / cosα = 1/0,59 = 1,7 м

Определение изгибающих моментов от поперечной нагрузки:

Мn = qxn •l²т/8 = 0,649•1,7²/8 = 0,23 кН•м

М = qx •l²т/8 = 0,749•1,7²/8 = 0,27 кН•м

Расчетная сжимающая сила: N= qу •lт = 1,028•1,7= 1,75 кН

2.3.2.4 Определение геометрических характеристик сечения

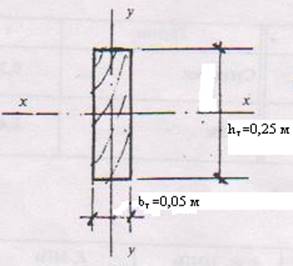
Арасч = hт•bт = 25•5=125 см²

Wx = bт•hт²/6 = 5•25²/6 = 520,83 см³

Ix = bт•hт³/12 = 5•25³/12 = 260,42 см⁴

Радиус инерции тетивы относительно оси x-x ix = 0,289•hт =0,289•250= =72,25 мм

Расчетная свободная длина тетивы l0= lт =1700 мм

Гибкость тетивы λ x = l0 • ix =1700/72,25=23,5, тогда φ, при λ<70

φ = 1-0,08(λ²/100)=1-0,08(23,15²/100)= 0,571

2.3.2.5 Проверка прочности тетивы

σ = N/Aрасч+Μд/Wx ≤ Ru, где Μд – изгибающий момент от действия поперечных и продольных