Определение удельного заряда электрона методом магнетрона (Методическое пособие по выполнению лабораторной работы)

Лабораторная работа

№3

“ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ МАГНЕТРОНА”

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ МАГНЕТРОНА

Цель работы

Определить удельный заряд электрона  по его движению во взаимно перпендикулярных электрическом и магнитном полях.

Введение

В данной роботе отношение  для электрона определется с помощью метода, который получил название "метод магнетрона". Это название связано с тем, что конфигурация электрического и магнитного полей, которая  используется, напоминает конфигурацию полей в магнетронах - генераторах электромагнитных колебаний в области сверхвысоких частот.

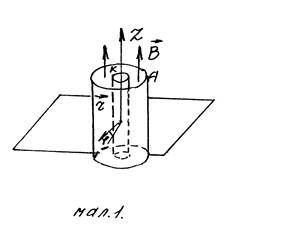Движение электронов в этом случае происходит в кольцевом пространстве, которое находится между катодом и анодом двухэлектродной лампы. Нить накаливания (катод) расположена вдоль оси цилиндрического анода, таким образом, что электрическое поле направлено по радиусу (рис.1). Лампа расположена внутри соленоида, который создает магнитное поле параллельное катоду. Рассмотрим траекторию электронов в такой комбинации полей.

Предположим, что начальная (тепловая) скорость электрона, с который он вылетает из катода, равна нулю. Тогда при заданной конфигурации полей движение электрона будет происходить в плоскости, которая перпендикулярна магнитному полю. Воспользуемся полярной системой координат. В этом случае положение электрона характеризуется расстоянием от оси цилиндра  и полярным углом .

Запишем уравнение движения электрона в плоскости () воспользовавшись уравнением для момента импульса электрона :

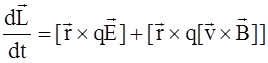,                                                     (1)

где  - заряд электрона,  - напряженность электрического поля между катодом и анодом,  - индукция магнитного поля.

Если рассмотреть электроды лампы как цилиндрический конденсатор, то модуль электрического поля  изменяется с расстоянием по закону:

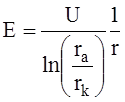,                                  (2)

где  - радиус анода,  - радиус катода.

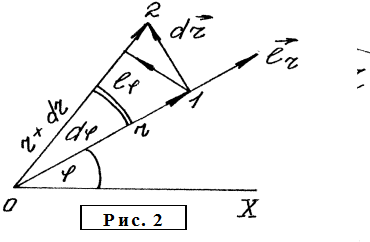
Момент силы  равен нулю, так как . Спроектируем уравнение (1) на ось . Для определения проекции момента силы Лоренца на ось  рассмотрим перемещение электрона в полярной плоскости () на величину  (рис. 2).

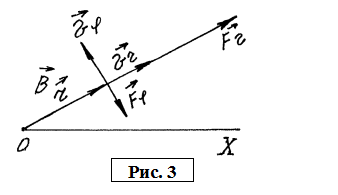
На рис. 3 показаны орты радиус-вектора  и полярного угла:  -  и  соответственно. Тогда вектор скорости

                                     (3)

Существование двух составляющих скорости  и  приводит к двум составляющим силы Лоренца:

           (4)

              (5)

Момент силы  относительно оси  равен , при этом учтено, что .

Таким образом, уравнение (1) принимает вид:

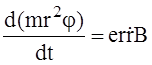                                                                  (6)

Проинтегрировав это уравнение, мы получим

                                                             (7)

где константа  - постоянная интегрирования, которая определяется начальными условиями.

Радиус катода  - малая величина, поэтому вначале движения электрона радиальная координата электрона  тоже мала. Правая часть уравнения (7) и первый член его левой части тоже мал. Поэтому постоянную интегрирования С с некоторой точностью можно положить равной нулю. Уравнение (7) при этом принимает вид:

.                                                                                    (8)

Таким образом, угловая скорость вращения электрона линейно зависит от индукции магнитного поля и при заданной индукции магнитного поля является постоянной величиной.

Далее рассмотрим радиальное движение электрона. Работа сил электрического поля при перемещении электрона от катода до точки с разностью потенциалов  равна:

.                                                                                            (9)

Магнитное поле работы не совершает. Поэтому кинетическая энергия электрона равна работе электрического поля (9) (при условии, что начальная скорость электрона при  равна нулю):