Санкт-Петербургский Колледж Морского Приборостроения
Выполнил: Студент гр. М-440
Проверила:
2004
Простые проценты
Рассмотрим однократного представления некоторой суммы Р в кредит на время t. За использование кредита надо платить. Возврат кредита составит S=P+I. Плата I (interest) носит название «процент». (В русском языке слову «процент» соответствуют два английских: «percent» и «interest».) Каким выбрать величину процента? С одной стороны, чем больше предоставленная сумма P, тем выше процент. Логичнее всего положить процент пропорциональным P. С другой стороны, чем больше время, на которое выдается кредит, тем больше процент. Опять-таки естественно предположить, что плата за кредит пропорциональна времени его использования. В результате приходим к формуле I=rPt. Здесь r- коэффициент пропорциональности – носит название «процентная ставка».
В каких же единицах мы будем измерять величины, входящие в формулу? Безусловно, I и P измеряются в денежных единицах: рублях, долларах, марках… А вот время измеряется, конечно в секундах и часах, ведь кредит предоставляется на достаточно длительный срок. Как правило, время измеряют в годах. Причем количество лет может быть и нецелым, тогда используются доли года. Размерность процентной ставки r (rate of interest) -1/год. Никто, однако, не говорит: «Ставка составляет 0,06 в год». Принято говорить так: «Ставка составляет 6% годовых в рублях».
Величина наращенной суммы (accumulated value) определяется по формуле S=P(1+rt). В этой формуле примем, что t=1 год, тогда S=P(1+r). Отношение S/P носит название «коэффициент наращения».
Немного потренируемся. Что означает 50% годовых? – S=P(1+0,5)=1,5 P, т.е. наращенная сумма в полтора раза больше первоначальной. А во сколько раз вырастет исходная сумма при 500% годовых? В шесть раз. (Можно сказать иначе: коэффициент наращения равен шести.)
Как проводить вычисления для вычисления для простых процентов? Начальная сумма Р задана, задана ставка процента r (причем надо проследить корректность размерности: ставка должна быть отнесена к году). Время нужно выразить в долях года. Заметим, что день выдачи ссуды и день погашения считаются одним днем. Поэтому, если мы хотим вычислить точное число дней ссуды, нужно просто вычесть дату выдачи из даты погашения и не корректировать результат прибавлением единицы.
Доля года вычисляется по формуле n=t/K, где t – число дней ссуды, К – число дней в году, или временная база.
Вы должны знать что измерение времени в финансовых расчетах – дело непростое. Здесь возможны различные условные соглашения.
Пример 1.
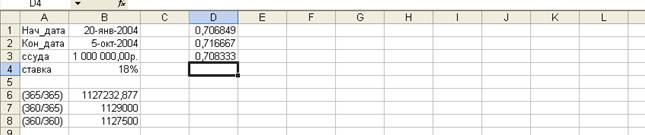
Ссуда в размере 1 млн руб. выдана 20 января до 5 октября включительно по 18% годовых. Какую сумму должен заплатить должник в конце срока?
Решение. Формулировка задачи нуждается в уточнении: в каком году производятся операции: в обычном или високосном. Но как мы уже видели, функция ДОЛЯГОДА работает без учета этого обстоятельства. Рассмотрим три варианта (рисунок 1).
Обратимся к финансовым функциям.
Книги по финансовой математике обычно открываются картинкой (рисунок 2).
При использовании финансовых функций приведенный рисунок неверен, так как показывает лишь абсолютные величины сумм. Правильны следующие две схемы, изображенные на рисунке 3.
На левом рисунке показана схема с точки зрения дебитора. Он получил в свое распоряжение сумму Р (знак положительный), а в конце периода Т должен вернуть эту сумму с процентами. Он лишается этой суммы, но с точки зрения кредитора. В начале периода Т он лишается суммы Р, а в конце возвращает ее с процентами. При использовании финансовых функций надо учитывать знаки денежных сумм, помня, с чьей точки зрения рассматривается финансовая операция – кредитора или дебитора. Поэтому современное и будущее значения связаны соотношением.
S+P(1+rt)=0
из которого ясно, что S и P должны иметь противоположные знаки.
Время в финансовых функциях измеряется в периодах. Границы периодов – это моменты платежей. Период может составлять год, квартал, месяц, день.
Тогда r=I/P носит название процентная ставка (interest rate), а d=I/S – ставка дисконта (discount rate). Легко получить между ними соотношение r=d/(1-d). Обычно процентную ставку относят к фиксированному периоду (как правило, году). Начисление по схеме простых процентов (simple interest) производится по формуле S+P(1+rT)=0, а по схеме сложных процентов (compound interest) по формуле S+P(1+r)T=0. Здесь r – процентная ставка за период, а Т – время, измеряемое
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.