Типы квантования непрерывных сигналов. Основы теории z-преобразования. Анализ устойчивости и точности дискретных систем. Частотные характеристики дискретных систем

ЛЕКЦИИ ПО КУРСУ

“ДИСКРЕТНЫЕ СИСТЕМЫ

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ”

 

Комсомольск-на-Амуре  2003

1. ОБЩИЕ СВЕДЕНИЯ

1.1 Типы квантования непрерывных сигналов.

Наряду с непрерывными системами автоматического управления (САУ) широкое применение находят системы, в которых имеет место дискретный способ передачи и преобразования дискретных сигналов. Процесс преобразования непрерывных сигналов в дискретные называется квантованием. Дискретность сигналов может быть обусловлена их квантованием по времени, по уровню или одновременно по уровню и по времени. По этому признаку дискретные системы подразделяются на три вида.

1. В импульсных системах в результате квантования по времени непрерывного сигнала  формируется последовательность его дискретных значений (дискрет), соответствующих фиксированным моментам времени. Обычно эти моменты отстоят друг от друга на постоянную величину , называемую интервалом квантования по времени (рис. 1). При этом сформированную последовательность дискрет принято называть решетчатой функцией  целочисленного аргумента. Очевидно, что различным непрерывным сигналам может соответствовать одна и та же решетчатая функция (рис. 2). В тоже время при заданном интервале квантования   каждой функции  соответствует единственная решетчатая функция. В общем случае квантование сигнала по времени сопровождается потерей информации, так как решетчатая функция  не передает характер изменения непрерывного сигнала между моментами квантования.

 

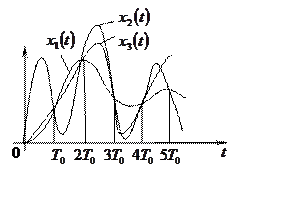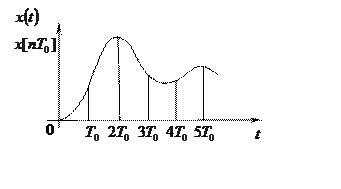Рис.1. Квантование непрерывного сигнала                       Рис.2. К определению решетчатой в импульсной системе                                                           функции

2. В отличие от квантования по времени, квантование по уровню может происходить в произвольные моменты времени, которым соответствует достижение непрерывного сигнала  заранее фиксированного уровня (рис. 3). Системы с таким типом квантования называются релейными.

3. Система, в которой имеет место квантование по уровню, и по времени, относятся к цифровым САУ (рис. 4).

Если величина интервала квантования много меньше диапазона изменения  сигнала , дискретностью по уровню можно пренебречь и тем самым свести цифровую систему к импульсной. Допустимость такой замены позволяет существенно упростить математическое описание дискретных систем. В дальнейшем под дискретными САУ в данном курсе подразумеваются только импульсные системы.

 

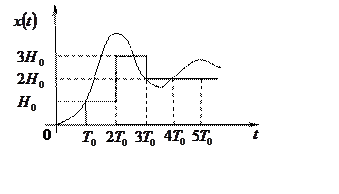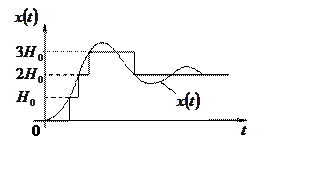Рис.3. Квантование непрерывного сигнала                       Рис.4. Квантование непрерывного сигнала в релейной  системе                                                                         по времени

( - интервал квантования по уровню)

1.2. Решетчатые функции разностные уравнения.

Очевидно, что для получения математического выражения, описывающего решетчатую функцию , необходимо в выражении для  выполнить формальную замену непрерывного аргумента t на . Например, непрерывной функции

будет соответствовать решетчатая функция

.

Для решетчатой функции определены ее разности. Первая обратная разность равна

, а первая прямая разность определяется выражением вида

.

Введем в рассмотрение прямую и обратную разности k-го порядка, которые определяются через разности (k-1)-го порядка по формулам:

;

соответственно. При управлении системой в реальном масштабе времени величина дискреты  не может быть определена в текущий момент времени , поэтому технически реализуется только обратная разность. Разности решетчатых функций являются аналогами производных для непрерывных функций времени.

Операцией, обратной операции взятия разности, является суммирование решетчатой функции, в результате которого получаем новую решетчатую функцию:

.

Уравнение вида

, в левой части которого записана комбинация решетчатых функций и ее разностей, называется разностным уравнением. Поскольку разность любого порядка может быть выражена в виде линейной комбинации значений решетчатой функции в различные моменты времени, для записи разностного уравнения используется следующая форма:

                                                                            (1)

Любое разностное уравнение может быть разрешено относительно значения решетчатой функции от наибольшего аргумента

                                                (2)

Очевидно, что (2) определяет рекуррентную процедуру численного решения разностного уравнения при известных начальных условиях .

Если комбинация решетчатых функций в (1) является линейной, то динамика дискретной системы описывается линейным разностным уравнением k-го порядка:

                                  ,                           (3)

в котором  - постоянные числа, если система стационарна, а - известная решетчатая функция, описывающая входное воздействие. Общее решение уравнения (3) представляет собой сумму общего решения однородного уравнения , полученного из (3) при , и частного уравнения , определяемого функцией :

                                                           .                                                     (4)

Первое слагаемое в (4), описывающее свободную составляющую движения