Ламинарный пограничный слой. Методы расчета ламинарного пограничного слоя, страница 2

Как было показано выше, в качестве масштабов удобно выбрать: для скорости – скорость потенциального течения U₀, для поперечной координаты у – толщину пограничного слоя d(х), возрастающую с увеличением координаты х. Тогда условие подобия профилей скорости можно записать в виде

,                                    (2.9) причем функция  должна быть одной и той же для всех расстояний х от передней кромки пластины.

Ранее [см. уравнение (1.31)], оценивая толщину пограничного слоя, мы нашли

;  ;  .               (2.10)

Поэтому за масштаб для у можно принять , откуда

.                               (2.11)

Часто при интегрировании уравнений пограничного слоя вводят функцию тока y(х, у), которая удовлетворяет уравнению неразрывности. Функция тока просто позволяет заменить две составляющие скорости Uи V одной функцией. Если определить функцию тока y(х, у) таким образом, чтобы

;   ,                                        (2.12)

то можно легко убедиться, что это определение удовлетворяет уравнению неразрывности

;       .                         (2.13)

Следуя Блазиусу, найдем масштаб для функции тока:

 

;                           .                           (2.14)

С учетом (2.9) и (2.11) имеем:

:  .

Подставляя эти значения в (2.14), получим

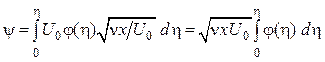.                (2.15)

Или можно переписать так:

 

,                                  (2.16)

где

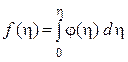                                     (2.17)

– безразмерная функция тока.                                                                                      (2.17)

Далее с учетом (2.14) и (2.16) выражаем продольную и поперечную скорости через безразмерную функцию тока.

Для продольной скорости

.                                     (2.18)

С учетом (2.16)

,                                 (2.19) где штрих у буквы f обозначает дифференцирование по h:

.

С учетом (2.12)

.                                     (2.20)

Подставив в (2.18) выражения (2.19) и (2.20), получим выражение для продольной составляющей скорости

.                           (2.21)

Для поперечной скорости имеем с учетом (2.16)

=

,                    (2.22)

но  , и тогда

.             (2.23)

Определим производные в квадратных скобках:

;

.                  (2.24)

Подставляя последние выражения в (2.23), получаем соотношение для поперечной скорости

,

                             (2.25)

Подставив (2.21) и (2.25) для продольной Uи поперечной Vскоростей в уравнение движения (2.7), найдем соотношение для определения безразмерной функции тока f(h). Сделаем это подробно: каждый член уравнения (2.7)

запишем в новых координатах:

:

;

;

.

:

V ® cм. уравнение (2.25);

;

;

= .

После подстановки полученных соотношений в уравнение движения запишем

,                  (2.26)

или после упрощения

.                                     (2.27)

Итак, мы получили обыкновенное дифференциальное уравнение. Граничными условиями на основании равенств (2.9), (2.21), (2.25) будут:

                              (2.28)

Применив аффинное преобразование (преобразование подобия), определяемое формулами (2.12) для η и (2.16) для функции тока ψ, мы заменили два уравнения в частных производных (2.7) и (2.8) одним обыкновенным дифференциальным уравнением для функции тока. Полученное уравнение – нелинейное, третьего порядка, следовательно, трех граничных условий (2.28) достаточно для полной определенности решения.

Уравнение (2.27) может быть решено либо путем разложения в ряд функции f(η), как это сделал Блазиус, либо численными методами. В табл. 2.1 приведены вычисленные Хоуартом значения функции f(η) и ее производных в зависимости от поперечной координаты η. Здесь в качестве примера приведены результаты расчета только для некоторых значений η. На самом деле расчеты выполнены в более широком диапазоне η.

Т а б л и ц а   2.1

Результаты решения позволяют вычислить все необходимые характеристики динамического пограничного слоя.

Распределение продольной скорости в соответствии с формулой (2.21) определяется первой производной от безразмерной функции тока

                     .                                      (2.29)

На рис. 2.2 расчетная кривая сравнивается с результатами опытов Никурадзе. Опытные точки получены на разных расстояниях от передней кромки пластины (Re_x = (1…7,3) 10⁵).

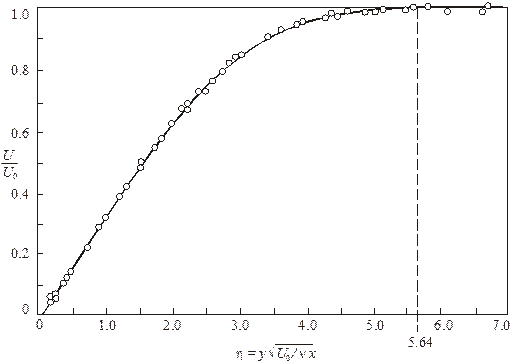
Рис. 2.2. Распределение скоростей в ламинарном пограничном слое на пластине: (о) – по измерениям Никурадзе; (–) – расчет по Блазиусу

Видно, что измерения хорошо подтверждают предсказанное теоретически подобие профилей скоростей на различных расстояниях х от передней кромки пластины.

Распределение поперечной скорости V, определяемое формулой (2.25)

показано на рис. 2.3.