Истечение жидкости из отверстий и насадок при постоянном напоре. Гидрогазодинамическая аналогия

Содержание отчета

1. Титульный лист.

2. Цель работы.

3. Схема экспериментальной установки.

4. Основные рабочие формулы.

5. Таблицы с результатами измерений и расчетов.

6. Графики ; .

ЛАБОРАТОРНАЯ РАБОТА № 3

ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ

И НАСАДКОВ

ПРИ ПОСТОЯННОМ НАПОРЕ

Цель работы

Определение опытным путем коэффициентов, характеризующих истечение жидкости через отверстия в тонкой стенке и через насадки при постоянном напоре.

Истечение из малого отверстия в атмосферу

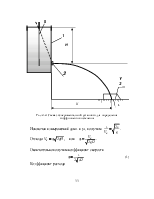
Как показывают опыты, картина истечения жидкости из некоторого сосуда через малое отверстие в вертикальной тонкой стенке имеет вид, изображенный на рис. 3.1, где обозначено: р₀ – давление на поверхности жидкости в сосуде; в общем случае р₀ не равно атмосферному давлению р_а; S – площадь отверстия; S_с – площадь сечения струи в некотором сечении С – С, называемом сжатым сечением (см. ниже); Н – заглубление центра тяжести ЦТ площади S отверстия под уровнем жидкости в сосуде; падением жидкости на расстоянии l₀ от стенки сосуда до сжатого сечения пренебрегаем, а поэтому считаем, что Н является также заглублением центра тяжести площади S_с под уровнем жидкости в сосуде.

Струя жидкости по выходе из отверстия резко сжимается на протяжении до сечения С – С. Такое сжатие обусловливается инерцией частиц жидкости, движущихся при подходе к отверстию по криволинейным траекториям (в частности, инерцией частиц, которые скользят непосредственно по стенке сосуда и, выйдя из него, движутся по границам струи).

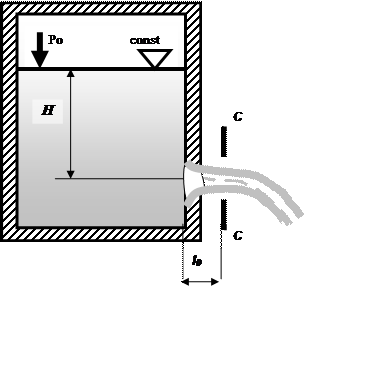Рис. 3.1. Схема истечения жидкости из отверстия

Если не учитывать возможной аэрации струи, т. е. насыщения ее пузырьками воздуха, а также не учитывать сопротивления воздуха, то надо считать, что за сжатым сечением С – С, в связи с увеличением скорости падающей жидкости, струя должна продолжать сжиматься, но относительно слабо.

Если скорость истечения жидкости из отверстия достаточно велика, то по боковой поверхности струи должны возникнуть большие касательные напряжения (приложенные к ней со стороны воздуха). Это сопротивление воздуха будет тормозить движение жидкости, ее скорости начнут уменьшаться, кроме того, она начнет аэрироваться, причем струя за сечением С – С будет расширяться. До сечения С – С имеется резко изменяющееся движение; после сечения С – С – плавно изменяющееся движение. Сечение струи по линии С – С и называется сжатым сечением.

Сжатое сечение С – С является тем первым (по течению) сечением, к которому можно прилагать уравнение Бернулли; к сечениям струи левее линии С – С уравнение Бернулли не применимо, так как движение здесь резко изменяющееся. Как показывает опыт, в сжатом сечении линии тока параллельны друг другу, причем скорости здесь распределяются равномерно.

Если отверстие круглое, то расстояние от внутренней поверхности стенки до сжатого сечения согласно имеющимся опытам будет

где D – диаметр отверстия.

Коэффициентом сжатия струи e называется отношение площади сжатого сечения S_C к площади отверстия S:

.

Найдем среднюю скорость V_с в сжатом сечении и расход Q жидкости, вытекающей из сосуда. Для решения этой задачи применяем уравнение Бернулли к двум сечениям: 1-1 и 2-2, из которых первое намечаем на уровне жидкости в сосуде и второе – по линии С – С. Плоскость сравнения проведем на уровне центра тяжести (ЦТ) площади S_с.

Уравнение Бернулли в известных нам обозначениях имеет вид:

Выясняем значения отдельных слагаемых, входящих в это уравнение:

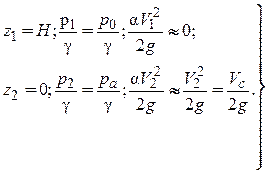
Скоростью движения жидкости в сосуде пренебрегаем. Подчеркнем, что давление в жидкости в сжатом сечении С – С равно атмосферному р_а.

Величину потерь напора Dh_f от сечения 1-1 до сечения 2-2 представим в виде

где z – коэффициент сопротивления, учитывающий потери напора от сечения 1-1 до сечения 2-2. Заметим, что потери напора сосредоточиваются в основном в районе самого отверстия, где скорости движения жидкости уже достаточно велики.

Получаем

Обозначим

где Н_пр можно назвать приведенным напором.

С учетом этого будем иметь

откуда

где

Коэффициент j, учитывающий уменьшение скорости в сжатом сечении за счет неравномерного распределения скоростей и потерь на трение, называется коэффициентом скорости.

В частном случае, когда р₀ = р_а, т. е. когда сосуд открыт,

Н_пр= Н,

при этом получаем

Для идеальной жидкости потери отсутствуют

т. е. в этом случае z = 0; j = 1,0.

Следовательно, для идеальной жидкости

Эта формула называется формулой Торричелли, по имени итальянского ученого, который впервые (в 1643 г.) установил экспериментальным путем данную зависимость, не учитывающую потери напора. В действительности, на практике коэффициент j близок к единице.

Зная скорость V_с в сжатом сечении, найдем расход Q для случая р₀ = р_а (сосуд открыт). Очевидно,

, где  называется коэффициентом расхода отверстия. Этот коэффициент учитывает и потери напора Dh_f, и степень сжатия