


















































Представленный лабораторный практикум содержит восемь лабораторных компьютерных работ по нескольким разделам физики: кинематика, динамика, электростатика, магнетизм, колебания и оптика.
Лабораторная работа 1кп
ИЗУЧЕНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ
НА МАШИНЕ АТВУДА
ВВЕДЕНИЕ
При движении тела, любая его точка описывает в пространстве линию, называемую траекторией. Если траектории всех точек тела представляют прямую, то движение называется прямолинейным. Если модуль (величина) скорости тела с течением времени увеличивается или уменьшается, то движение называется, соответственно, ускоренным или замедленным. Всякое ускорение есть результат действия на движущееся тело сил со стороны других тел. Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
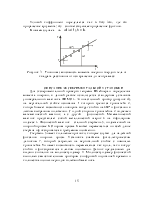
Схема экспериментальной установки на основе машины Атвуда приведена на рисунке 1.
На вертикальной стойке 1 крепится легкий блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. На корпусе среднего кронштейна имеется риска, совпадающая с оптической осью фотодатчика.
Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На вертикальной стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положения грузов. Начальное положение определяют по нижнему срезу груза, а конечное – по риске на корпусе среднего кронштейна. Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе. Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться.
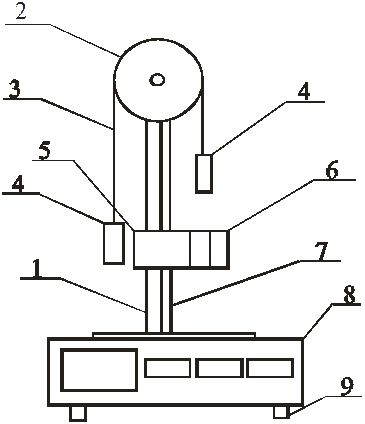
1 – стойка; 2 – блок; 3 – нить; 4 – грузы; 5 – средний кронштейн;
6 – фотодатчик; 7 – линейка; 8 – миллисекундомер; 9 – опора.
Рисунок 1 – Машина Атвуда
АНАЛИЗ ДВИЖЕНИЯ ГРУЗОВ В МАШИНЕ АТВУДА
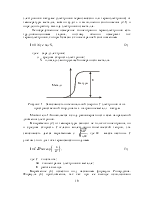
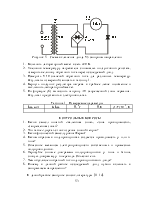
На рисунке 2 приведена схема, поясняющая принцип действия машины Атвуда. Совместим начало системы координат с осью блока и направим ось OX вертикально вниз. Обозначим массы грузов M, массу перегрузка - m. Предположим, что блок и нить невесомы, нить нерастяжима, сила трения мала. На каждый из грузов действует сила тяжести и сила натяжения нити.
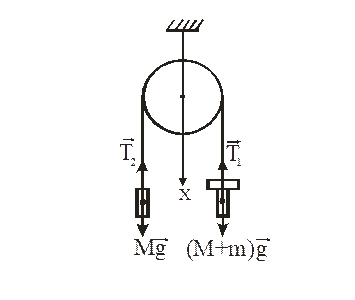
Рисунок 2 – Схема действия машины Атвуда
Уравнения движения грузов в скалярной форме имеют вид:
(M + m)·g – T1 = (M + m)·a1, (1)
Mg – T2 = M·a2.
В силу нерастяжимости нити a2 = - a1; при невесомом блоке T2 = T1. В итоге имеем следующую систему уравнений:
(M + m)·g – T1 = (M + m)·a1, (2)
Mg – T1 = - M·a1.
Решив эту систему относительно a1, получим
a1 = m·g/(m + 2M). (3)
Так как при данных M и m ускорение a1 постоянно по величине и направлению, то движение грузов будет равноускоренным. Ускорение a1 направлено вертикально вниз.
При равноускоренном движении с нулевой начальной скоростью справедливо выражение
S = at2/2, (4)
где S – путь, пройденный телом за время движения t,
a – ускорение движения.
Соотношение (4) можно проверить экспериментально, исследовав зависимость пути S от времени t. Однако, если проделав измерения, построить график зависимости S = f1(t) в координатах S и t, то мы получим некоторую кривую линию, по виду которой трудно утверждать, что эта кривая представляет собой параболу, соответствующую зависимости (4). В этой связи функцию (4) необходимо линеаризовать, т.е. выявить такие переменные, зависимость между которыми была бы линейной, и построить линеаризованный график. В данном случае такими переменными могут быть, например
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.