Методы экспертных оценок: Методические указания к выполнению практических работ по дисциплине «Методы получения и обработки информации для задач управления социально-экономическими системами»

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Сибирский государственный индустриальный университет»

Кафедра систем информатики и управления

Методы экспертных оценок

Методические указания к выполнению практических работ

Методические указания к выполнению практических работ по дисциплине «Методы получения и обработки информации для задач управления социально-экономическими системами» для специальности «Прикладная информатика (в управлении)» (351400).

Новокузнецк

2004

УДК: 669.01 – 035

М54

Рецензент:

Кандидат технических наук, доцент кафедры систем автоматизации

М54 Методы экспертных оценок: Метод. указ./Сост.: .: СибГИУ. - Новокузнецк, 2004. – 28с.

В данном методическом пособии рассмотрен следующие методы экспертных оценок: метод непосредственного оценивания объектов, метод парных сравнений объектов и метод априорного ранжирования факторов, методики обработки полученных результатов, приведены варианты заданий.

Методические указания предназначены для студентов специальности 351400  «Прикладная информатика (в управлении)»

Содержание

1.  Групповая экспертная оценка объектов при непосредственном оценивании. 4

1.1  Проведение опроса специалистов. 4

1.2  Обработка результатов экспертизы.. 5

1.3  Порядок выполнения работы.. 8

2.    Обработка парных сравнений. 10

2.1  Проведение опроса специалистов. 10

2.2  Обработка результатов экспертизы.. 11

2.3  Порядок выполнения работы.. 14

3.    Метод априорного ранжирования факторов. 19

3.1  Проведение опроса специалистов. 19

3.2  Обработка результатов экспертизы.. 19

3.3  Статистическая оценка достоверности экспертизы.. 20

3.4  Принятие решения о значимости факторов. 21

3.5  Порядок выполнения работы.. 21

4.    Список литературы: 27

 

1.  Групповая экспертная оценка объектов при непосредственном оценивании

1.1  Проведение опроса специалистов

Существует множество подходов к решению данной задачи. С целью иллюстрации рассмотрим один из простейших. Пусть т экспертов провели оценку п объектов по l показателям. Результаты оценивания представлены величинами , где i - номер объекта, j - номер эксперта, h - номер показателя. Величины , полученные методам непосредственного оценивания, представляют собой числа из некоторого отрезка числовой оси, или баллы.

В качестве групповой оценки для каждого из объектов можно принять среднее взвешенное значение его оценки

,  где q_h — коэффициенты весов показателей сравнения объектов, k_j — коэффициенты компетентности экспертов.

Величины q_h и k_j являются нормированными, то есть

Коэффициенты q_h  могут быть определены экспертным путем, как средний коэффициент веса h–го показателя по всем экспертам, то есть

Коэффициенты компетентности экспертов можно вычислить по апостериорным данным, то есть по результатам оценки объектов. Основной идеей этого вычисления является предположение о том, что компетентность эксперта должна оцениваться по степени согласованности его оценок с групповой оценкой объектов.

Коэффициенты компетентности экспертов можно вычислить по разным алгоритмам. Предлагаем алгоритм, сходимость которого доказана для случая, когда индивидуальные оценки неотрицательны, а эксперты и объекты не распадаются на отдельные группы (то есть когда каждая группа экспертов не оценивает объекты своей группы). В большинстве практических задач эти условия выполняются, что доказывает сходимость алгоритма.

1.2  Обработка результатов экспертизы

Пусть m экспертов оценили n объектов, используя одну и ту же шкалу интервалов. Тогда мы имеем матрицу оценок || x_ij ||, i=1, 2, …, n, j=1, 2, … m, где x_ij — оценка j-го эксперта для i-го объекта.

Алгоритм, предложенный Евлановым Л.Г. и Кутузовым В.А., основан на итеративной процедуре корректировки коэффициентов компетентности , j=1,2,…m, t=0,1,2,… - номер итерации. Этот алгоритм состоит из следующих основных процедур:

а) Первоначально на шаге t=0 значения коэффициентов компетентности равны между собой  , т.е. начальное значение коэффициентов компетентности для всех экспертов принимается одинаковым.

б) рекуррентные соотношения для t=1, 2, 3, ...

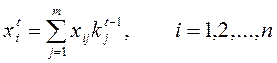 - групповая оценка для i-го объекта на t-ом шаге на основе индивидуальных оценок                                                                                                                                                     (1)

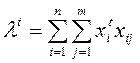 - нормировочный коэффициент                                                                                            (2)

 - коэффициенты компетентности j-го эксперта на t-ом шаге                                                                                           (3)

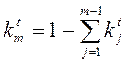 - коэффициенты компетентности m-го эксперта  из условия нормировки.                                                                             (4)

в) признак окончания итерационного процесса

Повторение рекуррентной процедуры вычисления оценок объектов и коэффициентов компетентности естественно ставит вопрос о ее сходимости. Для рассмотрения этого вопроса исключим из уравнений (1), (3) переменные  и , и представим эти уравнения в векторной форме:

,                                                                                                                (5)

где матрицы В размерности n´n и С размерности m´m равны:

                                                                                                                 (6)

Величина  в уравнениях (5) определяется по формуле (2).

Если матрицы В и С неотрицательны и неразложимы, то, как следует из теоремы Перрона-Фробениуса, при t®¥ векторы x^t и k^t сходятся к собственным векторам матриц В и С, соответствующим максимальным собственным числам этих матриц

.                                                                                                                (7)

Предельные значения векторов x и k можно вычислить из уравнений:

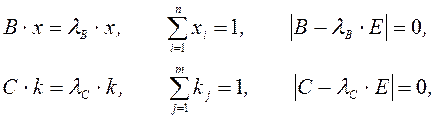                                                                                                                 (8)

где l_B и l_С - максимальные собственные числа матриц В и С, Е - единичная матрица.

Пример. Три эксперта (m=3) оценили значение двух мероприятий (n=2) по решению одной проблемы (l=1), приведя нормированные оценки x_1j+x_2j=1 объектов (таблица 1).

Таблица 1 – Нормированные оценки двух объектов тремя экспертами

Проведем вычисление групповых оценок мероприятий и коэффициентов компетентности экспертов по формулам (1), (2), (3). Средние оценки объектов первого приближения по формуле