Электрооптические свойства квантовых молекул и квантовых проволок с резонансными и локализованными донорными состояниями (Диссертация на соискание ученой степени кандидата физико-математических наук)

получения дисперсионного уравнения электрона, локализованного в поле регулярной цепочки D⁰-центров во внешнем продольном электрическом поле, воспользуемся граничным условием вида

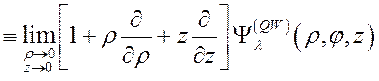.                     (3.2.41)

С учетом (3.2.40), получим

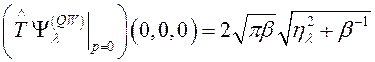.                           (3.2.42)

Действие оператора (3.2.41) на второе слагаемое в (3.2.39) приводит к появлению сумм следующего вида

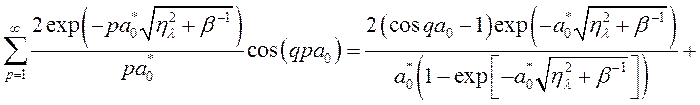
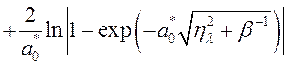,                                (3.2.43)

и

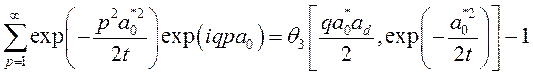,         (3.2.43)

где ,  – тэта функция Якоби [91].

Учитывая (3.2.42) и (3.2.43) дисперсионное уравнение, определяющее зависимость энергии связи локализованного электрона от параметров КП и величины внешнего электрического поля, запишется в виде

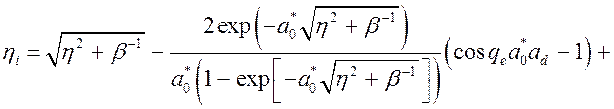
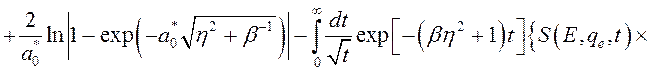
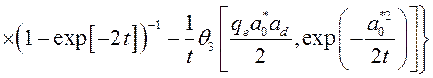,                   (3.2.44)

где  определяется выражением вида

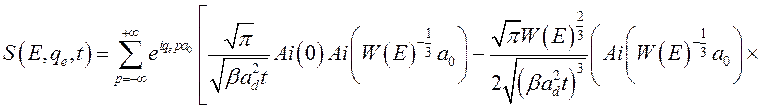
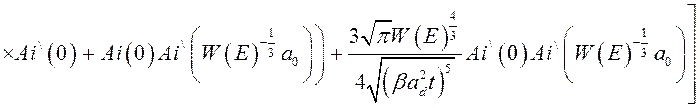, (3.2.45)

где  – первая производная функции Эйри [91].

При  и  уравнение (3.2.44) распадается на два уравнения определяющие границы примесной зоны:

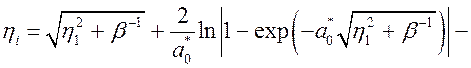
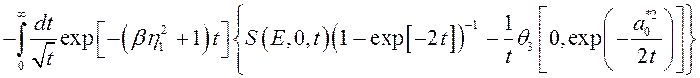,  (3.2.46)

и

          

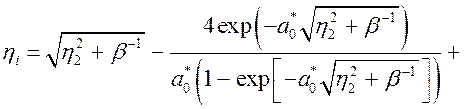
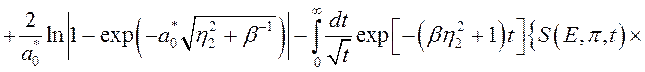
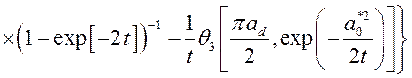        .                        (3.2.47)

При этом ширина примесной зоны  определяется как . В разделе 3.3 с помощью дисперсионных уравнений (3.2.46) и (3.2.47) будет исследована зависимость ширины примесной от периода регулярной цепочки D⁰-центров в КП и величины внешнего продольного электрического поля.

3.3 Зависимость ширины примесной зоны от периода регулярной цепочки D⁰-центров и величины внешнего электрического поля

На рис. 20 представлена зависимость ширины примесной зоны De в КП на основе InSb от величины напряженности E электрического поля для различных значений периода цепочки , нормированного на эффективный боровский радиус. Видно, что с ростом величины внешнего электрического поля ширина примесной зоны увеличивается за счет увеличения степени перекрытия одноцентровых волновых функций. Подобная ситуация имеет место и с уменьшением периода регулярной цепочки -центров (сравн. кривые 1 и 2 на рис. 20).

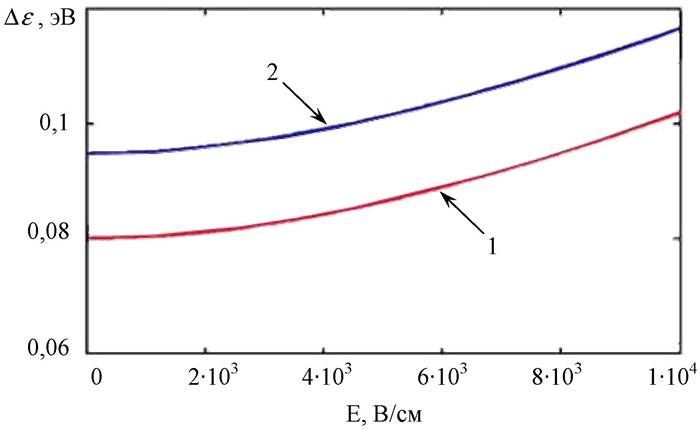
Рис. 20 Зависимость ширины примесной зоны в КП на основе InSb от величины напряженности электрического поля E, при U₀ = 0,3 эВ; E_i = 5·10^–3эВ; L = 70 нм:

1 – a₀ = 35 нм,

2  – a₀ = 28 нм.

Используя уравнение (3.2.44) можно получить в рамках рассматриваемой модели выражение для эффективной массы  электрона в поле одномерной цепочки D⁰-центров в КП:

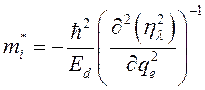.                                    (3.3.1)

Параметр , определяющий энергию связи примесного электрона в поле регулярной цепочки определяется из дисперсионного уравнения:

               

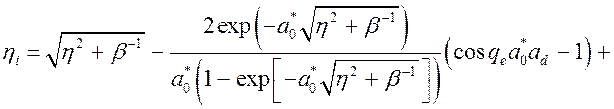
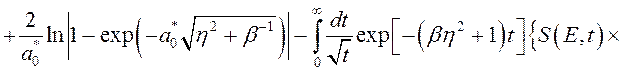
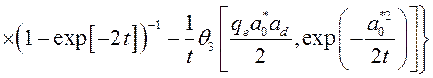             ,                     (3.3.2)

Дифференцируя  по q_e, как неявно заданную функцию, получим

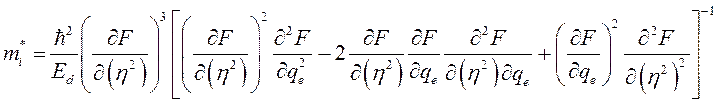, (3.3.3)

где

               

         

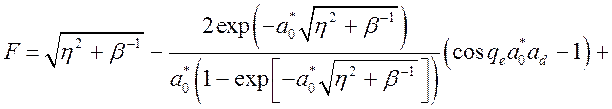
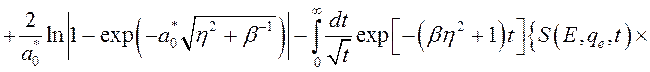
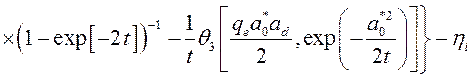.                   (3.3.4)

Для производных в (3.3.3) будем иметь:

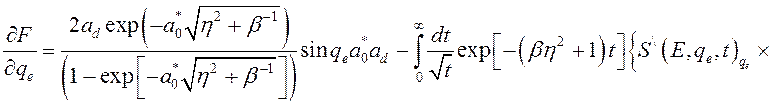
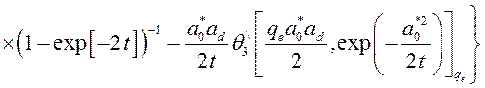,                 (3.3.5)

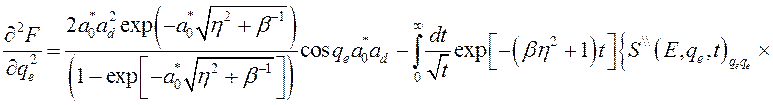
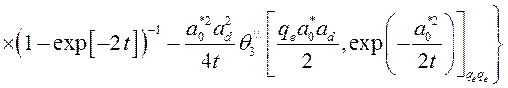,             (3.3.6)

       

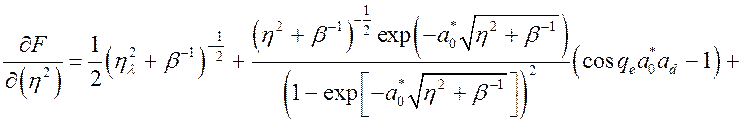
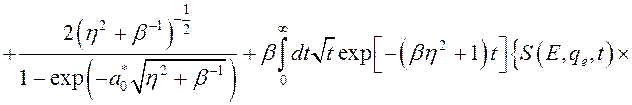
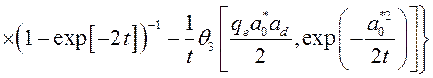                       ,                          (3.3.7)

     

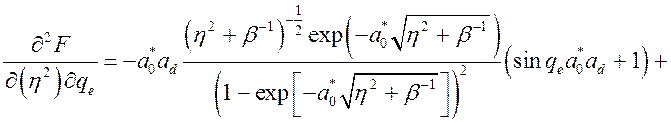
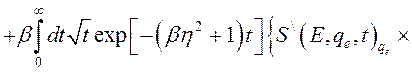
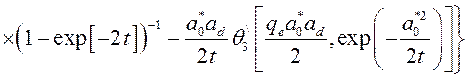                                        ,                    (3.3.8)

         

  

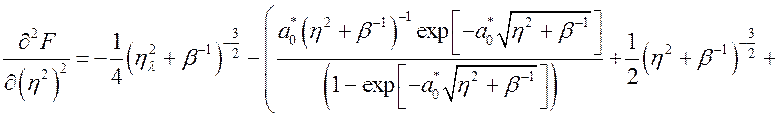
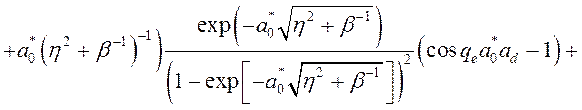
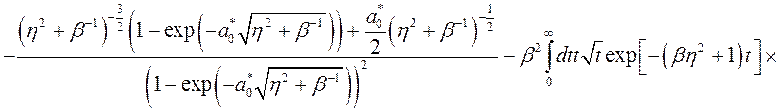
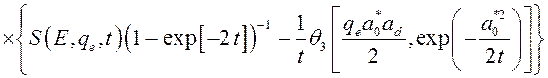                    .       (3.3.9)

На рис. 21 приведена зависимость эффективной массы , нормированной на эффективную массу электрона  в зоне проводимости КП, от периода цепочки  и величины внешнего электрического поля.

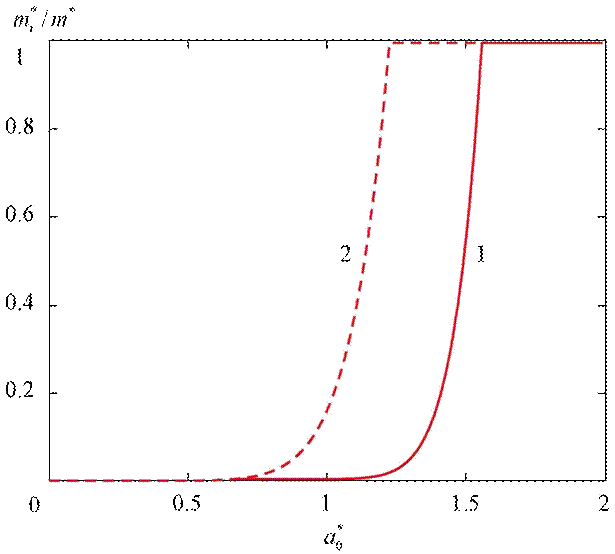
Рис. 21 Зависимость эффективной массы примесного электрона от периода регулярной цепочки -центров  и величины напряженности внешнего электрического поля  при эВ; ; :

1 – ,

2 –  В/м.

Из рис. 21 видно, что с ростом величины внешнего электрического поля  возрастает и, когда период регулярной цепочки становится больше эффективного боровского радиуса электрона,  становится равной эффективной массе электрона в зоне проводимости КП.

Получим выражение для нормированной волновой функции электрона , локализованного в поле регулярной цепочки -центров в КП. Согласно (3.4.26) и (3.4.27) имеем

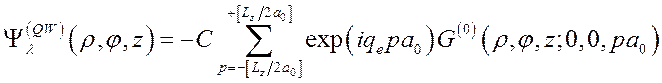, (3.3.10)

где  – нормировочный множитель.

В выражении (3.3.10) под знаком суммы находится безразмерная одноэлектронная функция Грина:

,        (3.3.11)

где  – одноэлектронная функция Грина, определяемая выражением (3.2.34).

Условие нормировки запишется следующим образом:

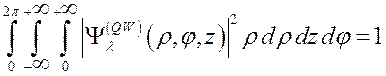,                 (3.3.12)

где

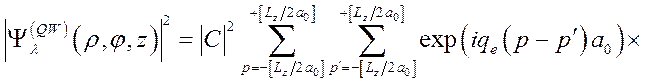
.                 (3.3.13)

Подставив (3.3.13) в (3.3.12) получим:

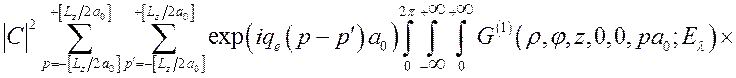
                    .                       (3.3.14)

Учитывая (3.2.22) для (3.3.13) будем иметь

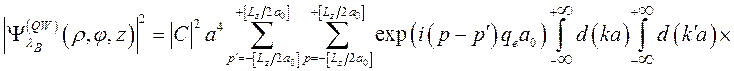
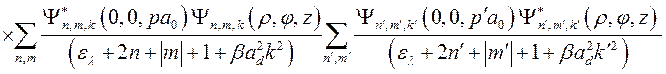,  (3.3.15)

в результате получим

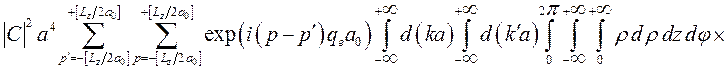
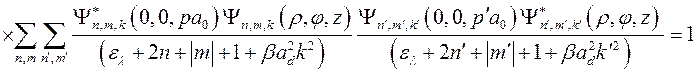,(3.3.16)

где .

Поскольку одночастичные волновые функции (3.2.22) образуют систему ортонормированных функций:

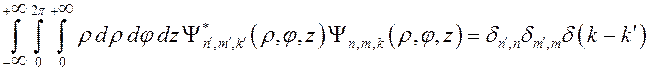,   (3.3.17)

где  – символ Кронекера:

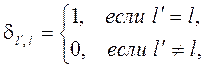                                     (3.3.18)

то условие нормировки (3.3.16) запишется в виде:

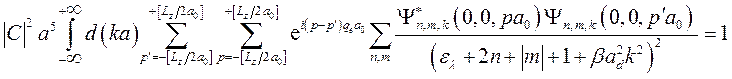. (3.3.19)

С учетом выражения для одночастичных волновых функций (3.2.22), получим

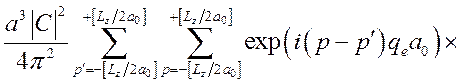
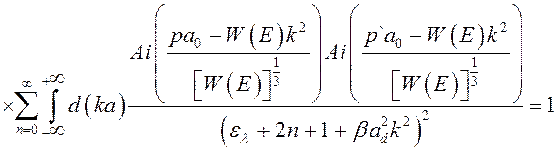.              (3.3.20)

Суммирование в (3.3.20) даёт [91]:

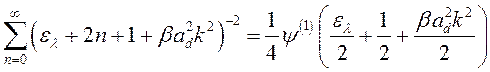,                (3.3.21)

где  – первая производная от -функции [91].

Тогда для нормировочного множителя получим

                  

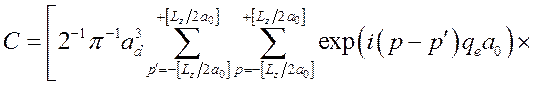
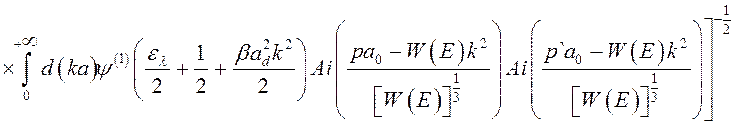. (3.3.22)

Найденная волновая функция электрона, локализованного в поле регулярной цепочки D⁰-центров и полученные дисперсионные уравнения, определяющие границы примесной зоны в КП во внешнем продольном электрическом поле, будут использованы в разделе 3.4 для расчёта спектров примесного поглощения света.

3.4 Расчёт спектров поглощения, связанных с переходами электрона из примесной зоны в размерно-квантованные состояния квантовой проволоки

Рассмотрим оптические переходы электрона из состояний примесной зоны в размерно-квантованные состояния КП при наличии внешнего продольного электрического поля. Волновая функция начального состояния имеет следующий вид

  

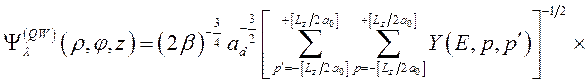
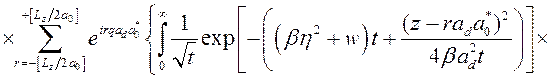
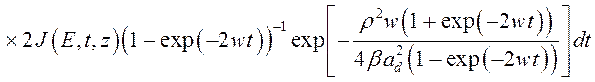,  (3.4.1)

где

.                                            

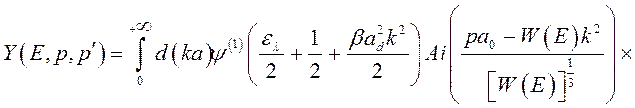
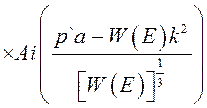Волновая функция конечного состояния определяется выражением (3.2.22).

Эффективный гамильтониан взаимодействия с полем световой волны запишется в виде (для случая ):

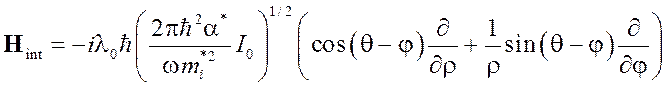, (3.4.2)

где l₀ – коэффициент локального поля, учитывающий различие амплитуд локального и среднего макроскопического полей; – интенсивность света; w –частота поглощаемого света; – постоянная тонкой структуры с учетом диэлектрической проницаемости материала КП;  – полярный угол единичного вектора поляризации; эффективная масса примесного электрона.

Тогда, выражение для матричного элемента , определяющего оптические переходы электрона из состояний примесной зоны в размерно-квантованные состояния КП, можно записать в виде

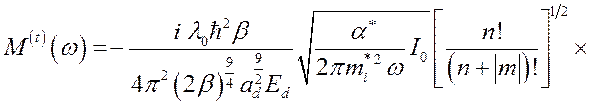
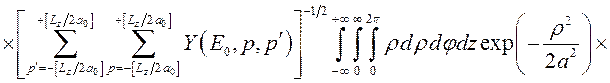
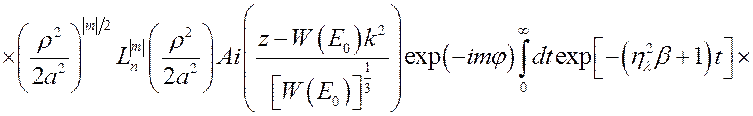
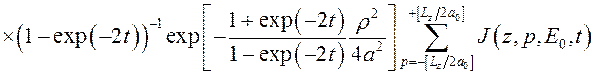,          (3.4.3)

При вычислении матричного элемента (3.4.3) появляется интеграл вида

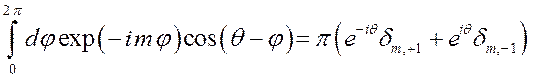,                (3.4.4)

где – символ Кронекера.

Учитывая правила отбора для магнитного квантового числа m, для интеграла по  в (3.4.3) получим

                      

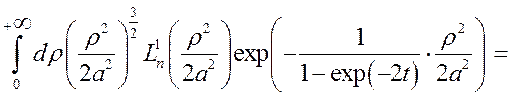
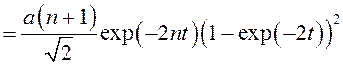.                              (3.4.5)

Интегрирование по z даёт

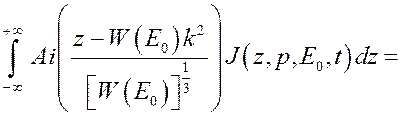
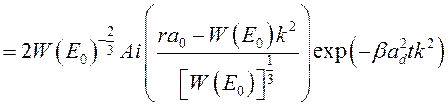,                     (3.4.6)

где было учтено, что [91]:

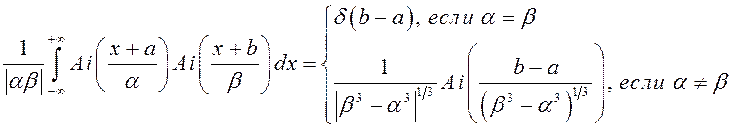
здесь  – дельта-функция Дирака [92].

С учетом (3.4.4), (3.4.5) и (3.4.6) матричный элемент (3.4.3) запишется в виде

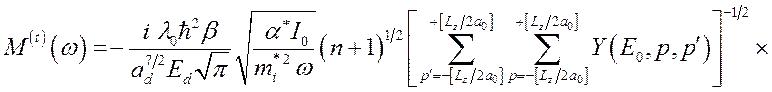
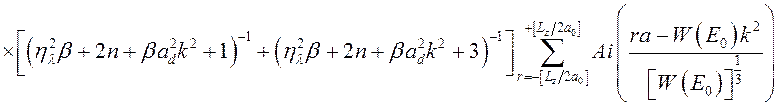. (3.4.7)

Вероятность оптического перехода электрона из состояний примесной зоны в размерно-квантованные состояния КП в продольном электрическом поле определяется как

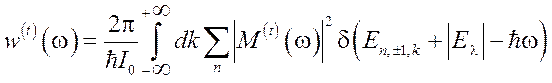.           (3.4.8)

Вычисление интеграла в (3.4.8) требует нахождения корней  аргумента -функции Дирака, удовлетворяющих закону сохранения энергии для рассматриваемых оптических переходов:

,              (3.4.9)

где  – энергия фотона в единицах эффективной боровской энергии