




















































Глава 5
МОДЕЛИ ПОГРЕШНОСТЕЙ АБСОЛЮТНОГО И ОТНОСИТЕЛЬНОГО СЧИСЛЕНИЯ. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
5.1 Модель погрешностей абсолютного счисления.
Прогнозирование случайных процессов
Прогнозирование случайного процесса
Случайные процессы с постоянным
математическим ожиданием. Прогнозирование случайного процесса Х(t) состоит в оценке будущих
ординат (значений) ![]() процесса по
прошлым и/или текущим его значениям. На рис.5.1.1 построен график случайного
процесса.
процесса по
прошлым и/или текущим его значениям. На рис.5.1.1 построен график случайного
процесса.
В интервале времени (t0, t1) наблюдался процесс, для момента t1+Θ необходимо найти прогнозируемое значение. В теории [23, 62, 98] известно несколько простых способов прогноза, из которых рассмотрим три:
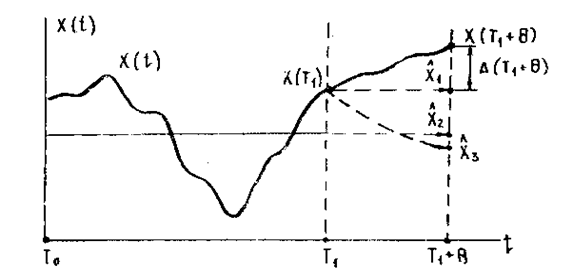
Рис. 5.1.1. Прогнозирование случайного процесса а) инерционный прогноз, или прогноз по последнему измеренному значению (х^1на рис. 5.1.1), при котором прогнозируемое значение и его СКП (без учета погрешностей измерения процесса) равны [62]:
x^1(T1 + ![]() ) = x(T1); m21(
) = x(T1); m21(![]() ) = 2m2x[1 –
) = 2m2x[1 – ![]() (
(![]() )]: (5.1.1)
)]: (5.1.1)
б) прогноз по математическому ожиданию (х^2 на рис.5.1..1) имеет два варианта:
![]() по
априорному значению математического ожидания, при котором [62]:
по
априорному значению математического ожидания, при котором [62]:
x^2(T1 + ![]() ) = Мx; m2(
) = Мx; m2(![]() ) = mx, (5.1.2,а)
) = mx, (5.1.2,а)
![]() по оценке математического
ожидания, полученной по этой же реализации на интервале времени t=T1–T0. В этом случае СКП прогноза
получается на основании теоремы о составляющих случайного процесса погрешностей (3.4.15):
по оценке математического
ожидания, полученной по этой же реализации на интервале времени t=T1–T0. В этом случае СКП прогноза
получается на основании теоремы о составляющих случайного процесса погрешностей (3.4.15):
x^2(T1+![]() ) = x*; m22(
) = x*; m22(![]() ) = m2х*
) = m2х*![]() + m2х[1–
+ m2х[1–![]() ], (5.1.2,б)
], (5.1.2,б)
где mх*= mх/![]() ; n – количество независимых измерений,
эквивалентное продолжительности времени t и определяемое по (3.4.7). в) статистический
прогноз по одной точке, или оптимальный прогноз (
; n – количество независимых измерений,
эквивалентное продолжительности времени t и определяемое по (3.4.7). в) статистический
прогноз по одной точке, или оптимальный прогноз (![]() на рис.3.2.1), при котором
на рис.3.2.1), при котором
x^3(T1 + ![]() ) = x* +
) = x* +![]() [x(T1) – x*]; m23(
[x(T1) – x*]; m23(![]() ) = m2x[1-
) = m2x[1-![]() 2(
2(![]() )], (5.1.3)
)], (5.1.3)
где x^j(t1+Θ) - прогнозируемое значение случайного процесса на интервал времени Θ; Мх – математическое ожидание процесса; x* - оценка математического ожидания (среднеарифметическое значение) процесса; ρ(Θ) - АКФ процесса, определяемая по текущей реализации или принимаемая априорно; х(T1) - последнее измеренное в момент Т1 значение процесса; mj(Θ) - СКП прогноза, являющаяся функцией времени прогноза Θ; mx - СКП случайного процесса.
Расчёты СКП m1(![]() ) и m3(
) и m3(![]() ) при разных значениях
) при разных значениях ![]() показывают, что эти СКП быстро
растут с увеличением времени прогноза
показывают, что эти СКП быстро
растут с увеличением времени прогноза ![]() . При
. При ![]()
![]() 0,5
0,5![]() К
наступает равенство m1(
К
наступает равенство m1(![]() )=m2(
)=m2(![]() ); с дальнейшим увеличением
); с дальнейшим увеличением ![]() становится m1(
становится m1(![]() )>m2(
)>m2(![]() ) и при
) и при ![]()
![]()
![]() К
наступает m1(
К
наступает m1(![]() )=1,4m2(
)=1,4m2(![]() ). Поэтому инерционный прогноз
должен быть прекращён при
). Поэтому инерционный прогноз
должен быть прекращён при ![]() =0,5
=0,5![]() К.
СКП оптимального прогноза растёт медленнее и равенство m3(
К.
СКП оптимального прогноза растёт медленнее и равенство m3(![]() ) = m2(
) = m2(![]() ) наступает при
) наступает при ![]()
![]()
![]() К
и далее СКП m3(
К
и далее СКП m3(![]() ) остаётся постоянной. Поэтому оптимальный
прогноз при
) остаётся постоянной. Поэтому оптимальный
прогноз при ![]()
![]()
![]() К
может быть прекращен.
К
может быть прекращен.
В навигации способы (5.1.1), (5.1.2,а), (5.1.3) используют, например, при прогнозировании точки местоположения корабля, сносимого с заданной линии пути течением, после выполнения обсервации. Способ (5.1.2,б) используют, например, в процессе фильтрации (совместной обработки обсервованных и счислимых координат).
Другие простые способы
прогноза (линейный и косинусный) не рассматриваем, т. к. они сложнее
инерционного и менее эффективны, чем оптимальный. Отметим только, что
продолжительность косинусного прогноза, реализованного в некоторых типах НК,
должна быть равна интервалу корреляции погрешностей прогнозируемого НП ![]() =
=![]() К.
Более сложные способы прогнозирования, например, статистический прогноз по двум
и более точкам, также не рассматриваем, т. к. при малом выигрыше в точности ВТ
<1 – 3% [62] сильно усложняются
К.
Более сложные способы прогнозирования, например, статистический прогноз по двум
и более точкам, также не рассматриваем, т. к. при малом выигрыше в точности ВТ
<1 – 3% [62] сильно усложняются
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.