Цифровые автоматы. Абстрактный синтез автомата, страница 6

 

Z0    Z1                                                                                Z0

 

A10                                                                                            A4

C                                                                                               W0

 

Z0,1

                                                                                                    Z0,1

A9     Z0                                                                                   A5

             W1                                                                                           W0

                           Z0                  Z1             Z0,1                 Z1         Z0

 

                                    A8                   A7         Z1        A6

                                    W0                   W1                    W1

3. МИНИМИЗАЦИЯ АВТОМАТА

Cовмесная минимизация методом АУФЕНКАНПА-ХОНА

	A1	A2	A3	A4	A5	A6	A7	A8
Z0	W0	W0	W0	W0	W0	W1	W0	W1
Z1	W0	W0	W1	W0	W0	W1	W1	W1

Табл.7

B11={a1a2a4a5}

B12={a3a7}

B13={a6a8}

	B11				B12		B13
	A1	A2	A4	A5	A3	A7	A6	A8
Z0	A2	A3	A5	A1	A4	A5	A6	A3
Z1	A8	A6	A6	A1	A7	A5	A6	A6

Табл.8

B12={a1} B22={A2} B23={A4} B24={A5} B25={A3} B26={A7} B27={A6} B28={A8}

Мы пришли к исходному кол-ву состояний, следовательно, автомат не минимизируется

Из имеющихся 4 автоматов выбираем автомат с минимальным числом состояний. Это полностью определенный автомат типа Мили, синтезированный по разметке входных  - выходных слов и имеющий 8 состояний.                      (см. сответсвующую таблицу)

4. СТРУКТУРНЫЙ СИНТЕЗ АВТОМАТА

Х ₁                                                                          Y₁

     . . .                                                          . . .            

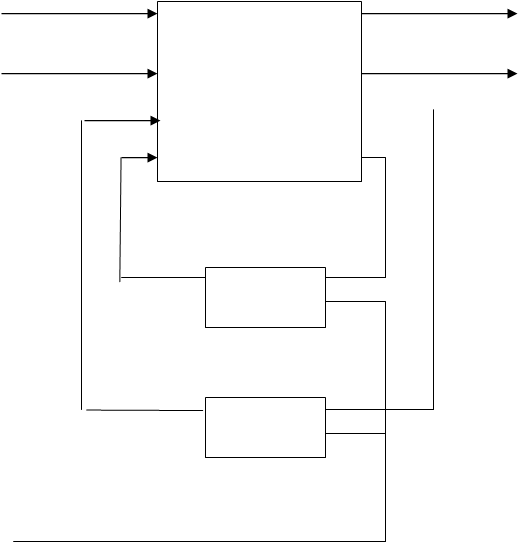
Х _L                                   КС                                Y_N

Q₁                          D₁

   ЭП₁

.

Q _R             :           D _R

    ЭП _n

                           C

Рис. 3

Структурный синтез представляет собой физическую реализацию схемы автомата из выбранного набора логических и запоминающих элементов, который бы функционировал в соответствии с заданной таблицей входов и выходов исходного абстрактного автомата.

Обобщёная схема синхронного автомата приведена на рис. 2. Структурный автомат имеет L входных каналов N выходных каналов и R элементов памяти. Автомат предлогается строить на логических элементах реализующих логические функции И, ИЛИ, исключающее ИЛИ НЕ на D-тригерах в качестве элементов памяти.

Поставим в соответствие каждой букве входного алфавита совокупность значений двоичных сигналов на входе структурного автомата. Аналогично надо закодировать выходные сигналы и внутренние состояния абстрактного автомата.

1. X₁ . . . X_L  -  входные сигналы

2^L  ³  F – Мощность  входного алфавита

Для данного случая F = 1  L = 1 т. е. число входов 1.

2. Y₁  . . . Y_N    -  выходные сигналы

2^N  ³  G – Мощность  выходного алфавита

Для данного случая G = 1  L = 1 т .е число выходов 1.