Возможности информационных технологий в научных исследованиях

Ярославский государственный педагогический университет

им. К. Д. Ушинского

Реферат по информатике на тему

«Возможности информационных технологий в научных исследованиях»

Выполнила: студентка гр. 815

ПЛАН

ВВЕДЕНИЕ

1. ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ

2. ЭВМ – СОАВТОР ОТКРЫТИЯ

3. ЛАЗЕРНЫЙ ТЕРМОЯДЕРНЫЙ СИНТЕЗ И ЭВМ

ЛИТЕРАТУРА

ВВЕДЕНИЕ

Модели реальных объектов, моделирование явлений издавна используются в науке и технике для проверки идей, отработки гипотез, получения экспериментального материала. За примером можно обратиться к авиастроению. Важным элементом проектной и конструкторской работы над новой машиной является выбор ее форм, оптимизация аэродинамических характеристик. Законченная теория здесь пока еще отсутствует, и этот недостаток приходится восполнять экспериментальными исследованиями. Однако экспериментировать с настоящими самолетами, отправляя машину в полет, который почти наверняка закончится аварией, – путь слишком расточительный и для летчика-испытателя опасный. Вот тут и приходят на помощь модели. И реальный самолет, и его уменьшенная копия в воздушном потоке подчиняются одним и тем же законам аэродинамики. При определенных условиях, измерив аэродинамические нагрузки на модели, оказывается возможным пересчитать их на “настоящий” летательный аппарат. Модель и самолет оказываются похожими не только внешне, но и по “физическому содержанию” – их аэродинамические характеристики связаны определенными соотношениями подобия.

Остается еще один шаг – не запускать модель в необъятное небо, а закрепить ее на специальном лабораторном стенде и направить на нее поток воздуха с той скоростью, с которой должна летать модель. Почти как в арифметике – от перемены скоростей воздуха и модели результат не изменится.

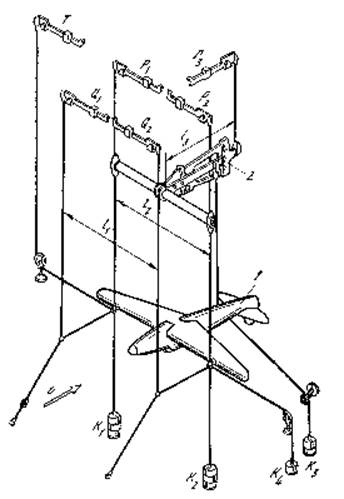
Рис. 1. Схема аэродинамических весов, предназначенных для измерения нагрузок, действующих на модель самолета в аэродинамической трубе

Так мы приходим к схеме аэродинамической трубы – установки, которая широко используется для экспериментального изучения воздействия потока газа на обтекаемый объект (рис. 1). Причем в качестве объекта может выступать не обязательно самолет, а и ракета, и мост, и высотное здание, и даже лыжник, прыгающий с трамплина. Конечно, приведенное описание аэродинамической трубы специалист сочтет чересчур кратким и, возможно, неточным, однако для нас главное состоит в том, чтобы подчеркнуть, что в основе такого рода исследований лежит метод моделирования, опирающийся в данном случае на строгую теоретическую базу, именуемую теорией подобия.

Итак, модель – это не только и нестолько внешнее сходство. Главное лежит глубже – поведение модели реального объекта должно подчиняться одинаковым закономерностям. Изучив их на доступной для исследования модели, оказывается возможным предсказать свойства проектируемой конструкции. Аэродинамическое моделирование относится к тому типу физического моделирования, когда и натурный объект, и модель имеют одинаковую физическую природу, в данном случае взаимодействие тела с воздушным потоком. Это естественный способ, но не единственный.

Представим себе, что, занимаясь строительной механикой, мы столкнулись с задачей определения напряжений, возникающих в балке призматической формы под действием крутящей нагрузки. Здесь, каким малым или большим бруском ни моделируй нашу балку, как его ни закручивай, выкрутишь немного. Ведь разместить внутри бруска достаточное количество датчиков, не повредив его и не повлияв тем самым на результат измерений, дело мудреное. И все же простая и в то же время эффективная модель для решения данной задачи существует. Изготовим трубу, сечение которой повторяет сечение интересующей нас балки. Торец трубы затянем резиновой пленкой – мембраной. Подадим в трубу воздух под некоторым давлением – мембрана выпучится наружу, прогнется. Вот модель закрученной балки и готова. Останется лишь тщательно промерить прогиб мембраны и с помощью несложных формул подобия вычислить величину напряжений в деформированной строительной конструкции.

На чем основывается уверенность, что полученный таким образом результат будет верным? Дело здесь в следующем. Математическая задача, описывающая напряженное состояние балки, в точности совпадает с задачей о прогибе мембраны. Только в одном случае функция, входящая в уравнение, есть напряжение, а в другом – прогиб мембраны (рис. 2). А раз задачи совпадают, то и решения у них одинаковы. Поэтому одно из них – форма вспучившейся мембраны, которая может быть измерена с хорошей точностью, – дает детальное представление о другом, недоступном для прямого наблюдения – распределении напряжений по сечению балки. Описанная “мембранная аналогия” дает пример физического моделирования одних явлений с помощью других, имеющих иную физическую природу.

рассуждая о физических моделях, мы вскользь упомянули о моделях совсем