
































Ключевые слова: граф, алгоритм, поиск, ширина, программа, аргумент, элемент, массив, очередь, память, время, сравнение.
Цель работы: Исследовать эффективность алгоритма поиска в графе в ширину.
Результат работы программы: количество сравнений элемента с ключом поиска и время, за которое был найден элемент по данному алгоритму поиска.
Областью применение данного алгоритма может быть разнообразна, на пример при построении карт местности: вершины графа – города, связи – дороги.
1. Краткая теория………………………………………………………..6 стр.
2. Анализ алгоритма……………………………………………………11 стр.
3. Спецификация задачи……………………………………………….14 стр.
3.1 Входные и выходные данные…………………………………14 стр.
3.2 Используемые процедуры…………………………………….14 стр.
4. Программа на языке Turbo Pascal..…………………………………15 стр.
4.1 Листинг программы…………..………….……………………15 стр.
4.2 Контрольный пример для тестирования №1….……………..26 стр.
4.3 Контрольный пример для тестирования №2….……………..26 стр.
4.4 Руководство пользователя…………………………………….27 стр.
5. Результаты тестирования……………………………………………28 стр.
Заключение………………………………………………………………33 стр.
Список используемой литературы……………………………………..34 стр.
Приложение А…………………………………………………………….35 стр.
Графы встречаются в сотнях разных задач, и алгоритмы обработки графов очень важны.
Существует множество разработанных алгоритмов для решения различных задач из самых разных областей человеческой деятельности. Формулировка задачи описывает, каким требованиям должно удовлетворять решение задачи, а алгоритм, решающий эту задачу, находит объект, этим требованиям удовлетворяющий. ([1])
В этой работе, мы не будем давать четкого определения алгоритма, а попытаемся проанализировать и изучить алгоритм поиска в ширину в графе.
Поиском по заданному аргументу называется алгоритм, определяющий соответствие ключа с заданным аргументом. Алгоритм поиска в ширину может быть использован для просмотра созданного графа, чтобы узнать состав информационных вершин для последующего поиска.
В результате работы алгоритма поиска заданная вершина может быть найдена или может быть отмечено отсутствие ее в исходных данных.
Если заданная информационная вершина найдена, то происходит вывод об успешном окончании поиска, вывод времени поиска и времени поиска ключа.
Очевидно, что наиболее понятный и полезный для человека способ представления графа — изображение графа на плоскости в виде точек и соединяющих их линий — будет совершенно бесполезным, если мы захотим решать с помощью ЭВМ задачи, связанные с графами. Выбор соответствующей структуры данных для представления графов имеет принципиальное влияние на эффективность алгоритмов, поэтому мы подробнее остановимся на этой проблеме. Мы покажем несколько различных способов представления и кратко разберем их основные достоинства и недостатки.
Мы будем рассматривать как ориентированные, так и неориентированные графы. Граф мы будем всегда обозначать G = (V,E), где V обозначает множество вершин, а Е — множество ребер, причем Е Í V X V для ориентированного графа и ЕÍ{{х,у}: х,у Î V ۸ х¹у} для неориентированного графа. Будем также использовать обозначения |V| = n и |Е| = m.
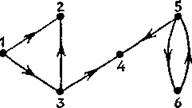
В теории графов классическим способом представления графа служит матрица инциденций. Это матрица А с n строками, соответствующими вершинам, и m столбцами, соответствующими ребрам. Для ориентированного графа столбец, соответствующий дуге <x, y> Î E, содержит —1 в строке, соответствующей вершине х, 1 в строке, соответствующей вершине у, и нули во всех остальных строках (петлю, т. е. дугу вида <x, x>, удобно представлять иным значением в строке х, например, 2). В случае неориентированного графа столбец, соответствующий ребру {х,у}, содержит 1 в строках, соответствующих х и у, и нули в остальных строках. Это проиллюстрировано на рис. 2.1. С алгоритмической точки зрения матрица инциденций является, вероятно, самым худшим способом представления графа, который только можно себе представить. Во-первых, он требует nm ячеек памяти, причем большинство этих ячеек вообще занято нулями. Неудобен также доступ к информации. Ответ на элементарные вопросы типа «существует ли дуга <x,y>?», «к каким вершинам ведут ребра из х?» требует в худшем случае перебора всех столбцов матрицы, а следовательно, m шагов.
Лучшим способом представления графа является матрица смежности, определяемая как матрица В = [b•j] размера nхm,
|
<1,2> |
<1,3> |
<3,2> |
<3,4> |
<5,4> |
<5,6> |
<6,5> |
(а)![]()
![]()
![]()
![]() 1 –1
–1 0 0 0 0 0
1 –1
–1 0 0 0 0 0
 2
1 0 1 0 0 0 0
2
1 0 1 0 0 0 0
3 0 1 -1 -1 0 0 0
4 0 0 0 1 1 0 0
5 0 0 0 0 -1 -1 1
6 0 0 0 0 0 1 -1
|
{1,2} |
{1,3} |
{1,5} |
{2,3} |
{2,5} |
{3,4} |
{4,5} |
{4,6} |
{5,6} |
![]() (б)
(б)![]()
![]()
![]() 1 1 1 1 0 0 0 0 0 0
1 1 1 1 0 0 0 0 0 0
2 1 0 0 1 1 0 0 0 0
3 0 1 0 1 0 1 0 0 0
4 0 0 0 0 0 1 1 1 0
5 0 0 1 0 1 0 1 0 1
6 0 0 0 0 0 0 0 1 1
![]()
![]()
Рис. 1. а) Ориентированный граф и его матрица инциденций;
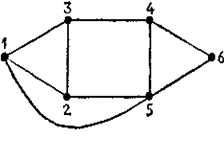
б) Неориентированный граф и его матрица инциденций.
где bij = 1, если существует ребро, идущее из вершины х в вершину у, и bij = 0 в противном случае. Здесь мы подразумеваем, что ребро {х, у} неориентированного графа идет как от х к у, так и от у к х, так что матрица смежности такого графа всегда является симметричной. Это проиллюстрировано на рис. 2.
Основным преимуществом матрицы смежности является тот факт
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.