Марковские процессы. Модель прогноза тенденции финансирования штатного состава фирмы

Предмет

«Аналитическая работа в органах гос и мун управления»

тема

«Марковские процессы»

СОДЕРЖАНИЕ

Введение

1. Основные понятия Марковских процессов

2. Марковские цепи

3. Модель прогноза тенденции финансирования штатного состава фирмы

3.1 Качественная модель

3.2. Прогноз возможности сохранения структуры через уравнения политикой фирмы

4. Экономическое применение

Заключение

Литература

Введение

Одним из важнейших факторов, который должен учитываться в процессе принятия оптимальных решений, является фактор случайности. При учете "случайности" необходимо, чтобы массовые случайные явления обладали свойством статической устойчивости.

Это означает, что учитываемые случайные явления подчиняются определенным статическим закономерностям, требования которых не обязательны при учете неопределенности.

Условие статической устойчивости позволяет использовать в процессе принятия решений эффективные математические методы теории случайных процессов и, в частности, одного из ее разделов - теории Марковских процессов.[1]

Функционирование широкого класса систем можно представить как процесс перехода из одного состояния в другое под воздействием каких-либо причин. Например, процесс функционирования ЭВМ характеризуется тем, что в каждый момент времени обработкой информации заняты те или иные блоки. Процесс прохождения обрабатываемой информации по блокам ЭВМ можно рассматривать как процесс перехода системы из одного состояния в другое. В полной мере это относится и к процессу функционирования ЭВМ с точки зрения надежности.

В каждый момент времени некоторые узлы работоспособны, а некоторые отказали и восстанавливаются. Если каждому возможному множеству работоспособных (или отказывающих) элементов поставить в соответствие множество состояний системы, то отказы и восстановления элементов будут отражаться переходом объекта из одного состояния в другое. [4]

Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений, особое внимание Марковские процессы приобрели у специалистов, занимающихся исследованием операций и теорией принятия оптимальных решений.

Управление инвестиционным портфелем является типичной задачей исследования операций.

В ней присутствуют все атрибуты канонической постановки:

·  динамика цен на обращаемые бумаги рассматривается как случайный Марковский процесс с дискретным временем;

·  цель операции носит многокритериальный характер (ожидаемый выигрыш, риск, ликвидность и т.п.);

·  процесс развивается в динамике.

Несмотря на указанную выше простоту и наглядность, практическое применение теории Марковских цепей требует знания некоторых терминов и основных положений, на которых следует остановиться перед изложением примеров. [6]

1. Основные понятия Марковских процессов

Функция Х(t) называется случайной, если ее значение при любом аргументе t является случайной.

Случайная функция Х(t), аргументом которой является время, называется случайным процессом.

Марковские процессы являются частным видом случайных процессов. Особое место Марковских процессов среди других классов случайных процессов обусловлено следующими обстоятельствами: для Марковских процессов хорошо разработан математический аппарат, позволяющий решать многие практические задачи; с помощью Марковских процессов можно описать поведение достаточно сложных систем.

Определение. Случайный процесс, протекающий в какой либо системе S, называется Марковским, если он обладает следующим свойством: для любого момента времени  вероятность любого состояния системы в будущем (при ) и не зависит от того, когда и каким образом система S пришла в это состояние.

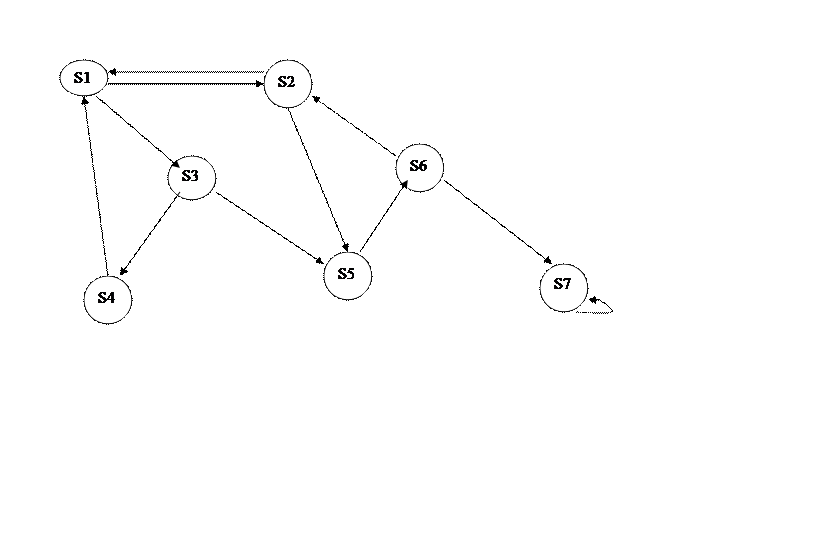
Рисунок 1 - Граф состояния системы S.

Классификация Марковских процессов. Классификация Марковских случайных процессов производится в зависимости от непрерывности и дискретности множества значений функций Х(t) и параметра t. Различают следующие основные виды Марковских случайных процессов:

- с дискретными состояниями и дискретным временем (цепь Маркова);

- с непрерывными состояниями и дискретным временем (марковские последовательности );

- с дискретными состояниями и непрерывным временем (непрерывная цепь Маркова);

- с непрерывным состоянием и непрерывным временем.

В данной работе будут рассматриваться только марковские процессы с дискретными состояниями S1,S2,….,Sn.

Граф состояний. Марковские процессы с дискретными состояниями удобно иллюстрировать