Расчет режима несимметричного короткого замыкания в сложной электрической сети

Дополнительно

Расчет коэффициентов распределения токов в элементах схемы замещения основан на правиле разброса токов, которое является следствием 1-го 2-го законов Кирхгофа, а также на законе Ома.

2. Расчет режима несимметричного короткого замыкания в сложной электрической сети

В практических расчетах несимметричных режимов используются те же допущения, что и при анализе симметричного трехфазного КЗ.

Расчет проведем в системе относительных единиц при тех же базисных условиях.

2.1 Схема замещения прямой последовательности

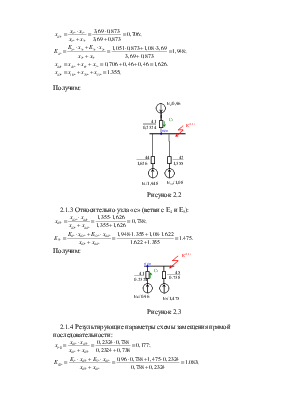
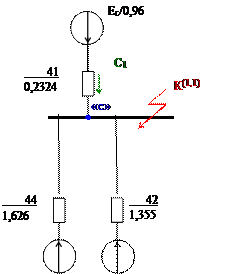
Сопротивление элементов и ЭДС источников питания в о.е. для исходной схемы представлены на рис.1.2. При расчете параметров  в процессе упрощения схемы максимально используем результаты П.1. В качестве исходной позиции принимаем схему, представленную на рис.1.3, с учетом преобразований показанных на рис.1.4.

Схема замещения прямой последовательности представлена на рис.2.1.

 

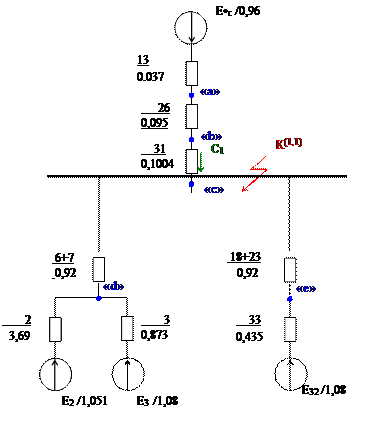Рисунок 2.1

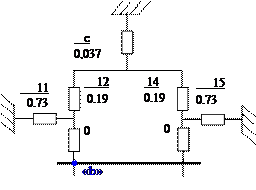
2.1.1 Преобразуем ветвь «Система» - «с»:

2.1.2 Преобразуем относительно узла «d» (ветви с Е₂ и Е₃):

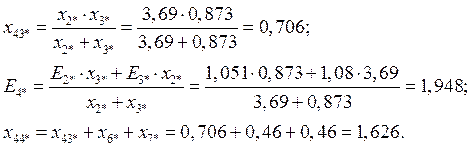
Получим:

				Е32/1,08
		Е4/1,948

 

Рисунок 2.2

2.1.3 Относительно узла «с» (ветви с Е₄ и Е₅):

41 0.2324

К(1,1)

С1

Е5/1,475

45 0.738

Получим:

	«с»

 

	Еc/0.96

 

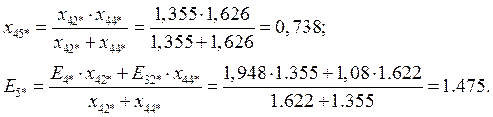
Рисунок 2.3

2.1.4 Результирующие параметры схемы замещения прямой последовательности:

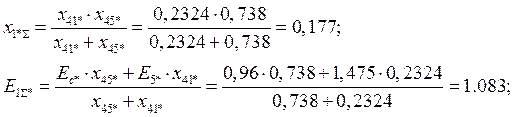
Получим:

			К(1,1)

 

X1∑

                        

 

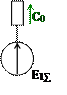Рисунок 2.4

2.2 Схема замещения обратной последовательности

Схема замещения обратной последовательности (рис.2.5) по структуре полностью совпадает со схемой прямой последовательности. Отличие схемы обратной последовательности состоит в том, что в ней ЭДС всех генерирующих источников питания принимаются равными нулю, а в месте КЗ приложено напряжение обратной последовательности (U_2k). В данных расчетах принимаем, что параметры схемы замещения обратной последовательности совпадают с параметрами схемы прямой последовательности, т.е.  

 

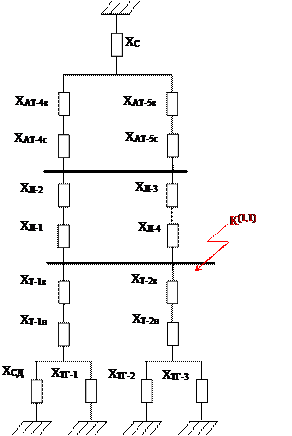Рисунок 2.5

2.3 Схема замещения обратной последовательности

Схема замещения нулевой последовательности (рисунок 2.6)существенно отличается от схемы прямой последовательности и в значительной мере определяется соединением обмоток трансформаторов. Сопротивления трансформаторов нулевой последовательности равны сопротивлениям прямой последовательности , а сопротивления линий для нулевой последовательности необходимо пересчитать в соответствии с данными таблицы П.2.1.

Л-1(), Л-2(), Л-3() – одноцепные линии со стальным тросом ();

Л-4() – двухцепная с хорошо проводящим тросом ().

 

Л3 0,09

Л2 0,1512

                                                                                

 

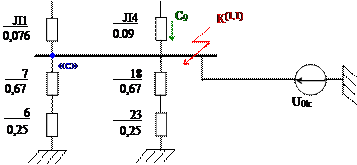Рисунок 2.6

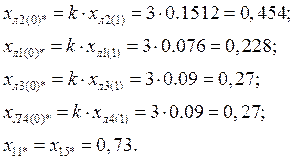
Преобразование  схемы:

2.3.1 Относительно узла «с» (ветви с Т-1 и Т-2):

.

2.3.2 Ветви, заключенные между узлами «b» и «c»:

2.3.3 Ветви между узлами «а» и «b»:

2.3.4 Относительно узла «b» (ветвь «Система» - «b»):

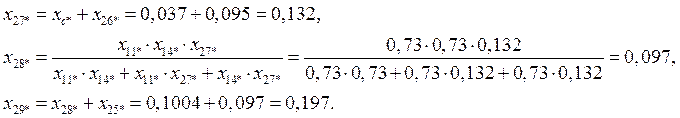
2.3.5 Результирующие параметры схемы замещения нулевой последовательности:

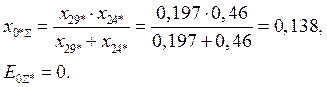
2.4 Расчет параметров аварийного режима для начального момента t=0

Согласно метода симметричных составляющих, расчет несимметричных КЗ приводит к правилу эквивалентности тока прямой последовательности, в соответствии с которым ток прямой последовательности любого несимметричного КЗ в реальной точке численно равен току трехфазного КЗ в некоторой фиктивной точке, удаленной от реальной точки на дополнительный реактанс

2.4.1. Дополнительный реактанс для двухфазного короткого замыкания на землю вычисляется по формуле [2, стр.62, табл.П2.2]:

тогда периодические слагаемые тока КЗ прямой, обратной и нулевой последовательностей для особой фазы  составят:

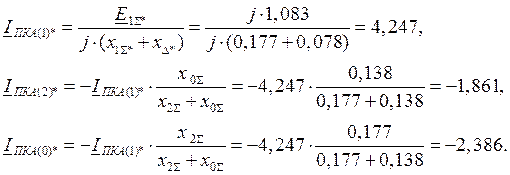
Для построения векторной диаграммы токов по месту КЗ находим       

-симметричные составляющие тока фазы А в именованных единицах:

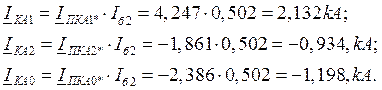
-симметричные составляющие токов поврежденных фаз:

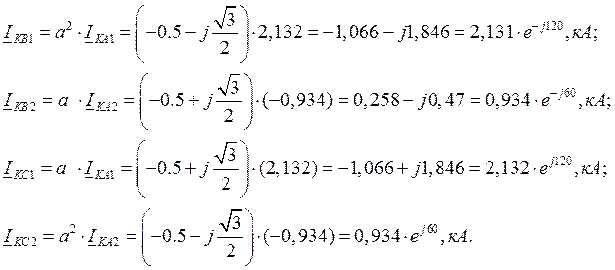
2.4.2 Расчет коэффициентов токораспределения:

- прямой последовательности:

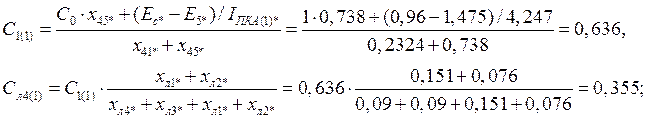
- обратной последовательности:

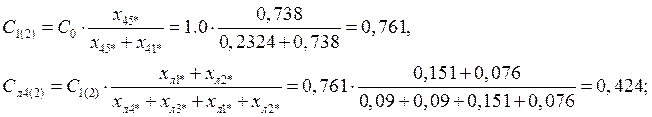
- нулевой последовательности:

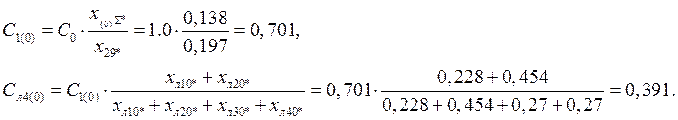
2.4.3 Вычисляем коэффициент пропорциональности m^(1,1) по формуле[2, табл.П2.2, стр.62]:

.

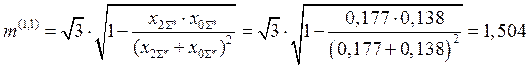2.4.4 Модуль периодической слагаемой тока поврежденных фаз в точке несимметричного КЗ определяется по выражению:

В именнованых единицах:

Ударный ток КЗ:

2.4.5 Расчет фазных токов протекающих в ВЛ-4:

Для ВЛ-4 имеем коэффициенты токораспределения:

Симметричные составляющие тока фазы А ВЛ-4 в расчете на одну цепь:

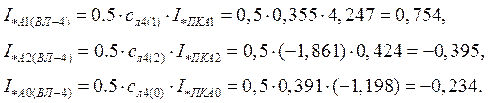
Фазные токи поврежденных фаз ВЛ-4 в именованных единицах: