Второй закон термодинамики. Анализ основных термодинамических процессов в идеальных газах

является полным дифференциалом, а функция s есть функция состояния системы и называется энтропией. Как функция состояния системы энтропия однозначно определяется любой парой термодинамических параметров состояния: s = s₁(p, v), s = s₂(p, T), s = s₃(v, T). Энтропия S для m кг газа равна: S = m×s, Дж/К.

За начало отсчета энтропии для газов принимают условное начало отсчета при температура Т=0 ^оС, для которого s₀=0.

За начало отсчета энтропии для воды и водяного пара принята так называемая тройная точка (Т=273.16 К и р=0.0006 Па).

Для расчета изменения энтропии идеального газа используются формулы:

Ds = s₂ – s₁ = c_vlnT₂/T₁ + Rln(v₂/v₁),                                         (1.32)

где c_v = const;  и

                                             Ds = c_plnT₂/T₁ – Rlnp₂/p₁,                                   (1.33)

где c_p = const.

Параметры u, h, s однозначно описывают любое состояние термодинамической системы и называются калорическими параметрами состояния. Между калорическими u, h, s и термическими p, v, T параметрами существует взаимно однозначное соответствие.

Если первый закон термодинамики в виде            

dq = du + pdv

объединить с dq =Tds из (1.31), то получим

Tds = du + pdv,                                      (1.34)

называемое термодинамическим тождеством или основным уравнением термодинамики.

1.8.3.Ts-диаграмма

Поскольку энтропия есть функция состояния произвольной термодинамической системы, то каждое ее состояние однозначно отображается точкой на плоскости T,s. Процесс в Ts-диаграмме изображается, как и в любой термодинамической диаграмме состояния, линией.

С помощью параметров состоянияр, v, T, а также u, h нельзя графически изображать количество теплоты так, как, например, можно изобразить работу в p,v-координатах. Энтропия как параметр состояния позволяет это сделать в Ts-координатах.

Из (1.31) для обратимых процессов имеем

dq = Tds                                             (1.35) или

q = òT(s)ds.                                            (1.36)

Для вычисления удельной теплоты процесса по формуле (1.36) необходимо знать функцию T(s). В Ts-координатах количество подведенной к системе (или отведенной от нее) теплоты в обратимом процессе изображается в виде площади под кривой процесса (рис.1.12), т.е.

q = пл. 1-2-s₂-s₁ = T(s)ds.                                      (1.37)

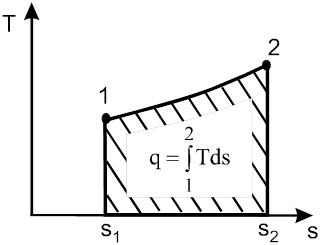Рис.1.12. Изображение теплоты процесса 1-2 в Ts-диаграмме.

Из (1.35) следует, что количество подведенной и отведенной теплоты зависит от характера процесса изменения энтропии. Если ds > 0, то dq > 0, т.е. теплота подводится к системе, и, наоборот, если ds < 0, то и dq < 0 – теплота отводится от системы.

Ts-диаграмма удобна и наглядна для анализа термодинамических процессов и циклов. При ее построении обычно за нуль энтропии условно принимается ее значение при температуре 0 ^оС=273.15 К и давлении 101325 Па.

1.8.4.Круговые процессы. КПД цикла

Цикл, в результате которого производится работа, называется прямым циклом или циклом теплового двигателя. Цикл, в результате которого расходуется работа, называется обратным или циклом холодильной машины.

Циклы, состоящие только из равновесных обратимых процессов, называются идеальными. Если один из процессов, составляющих цикл, необратим, то и весь цикл будет необратимым.

По определению равновесного процесса равновесный подвод и отвод теплоты предполагают равенство или бесконечно малую разницу температур между горячим и холодным источниками и рабочим телом в каждой точке процесса. Следовательно, для осуществления равновесного обратимого идеального цикла необходимо иметь рабочее тело, совершающее круговой процесс с функцией T(s), и соответствующий этой функции набор горячих и холодных источников теплоты q₁(T₁) и q₂(T₂).

Для прямого обратимого цикла теплового двигателя q₁ > 0, а q₂ < 0, и суммарное количество теплоты, полученное рабочим телом за цикл, составит

q_ц = q₁ – q₂, где q₁ и q₂ – соответственно подведенная и отведенная теплота.

Запишем уравнение первого закона термодинамики для данного случая:

q_ц = Du + l_ц.

Объединяя эти два уравнения, с учетом того, что для обратимого цикла  òdu = Du = 0, получим

l_ц = q₁ – q₂,                                                                           (1.38)

т.е. алгебраическая сумма подведенной и отведенной за цикл теплоты перешла в работу цикла. Ясно, что работа равновесных обратимых циклов максимальна, поскольку они являются по определению идеальными.

Если же цикл будет необратимым из-за необратимости хотя бы одного из составляющих его процессов, то появляются дополнительные внутренние потери теплоты на трение, вихреобразование и др. Это приводит к увеличению q₂ и, соответственно, к уменьшению (q₁ – q₂), т.е. к уменьшению работы цикла l_ц. Следовательно, работа необратимого цикла меньше работы обратимого