Расчет изгибающегося момента на левой опоре балки. Построение эпюры прогибов

Задача 10

Для балки требуется: 1) найти изгибающий момент на левой опоре (в долях ); 2) построить эпюры  и ; 3) построить эпюру прогибов, вычислив три ординаты в пролете и две на консоли.

Решение

Момент на опоре

Балка один раз статически неопределима. Для раскрытия неопределимости и определения изгибающего момента на левой опоре выберем в качестве основной схемы балку, лежащую на двух опорах. В эквивалентной схеме приложим неизвестный изгибающий момент  на левой опоре. Чтобы его определить составим каноническое уравнение метода сил

Для определения угла поворота  от единичного момента и угла поворота  от заданной нагрузки, постоим эпюры изгибающих моментов в основной системе при единичном и грузовом состоянии.

Построим единичную эпюру . Значения на границах участков

Для построения грузовой эпюры  вычислим реакции от заданной нагрузки

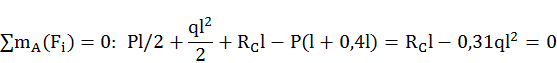
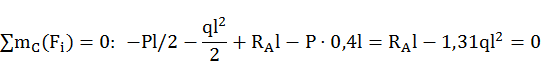
Тогда значения на границах участков силовой эпюры

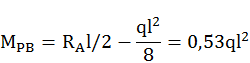
Определим  и  по правилу Верещагина

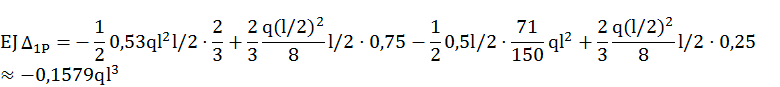
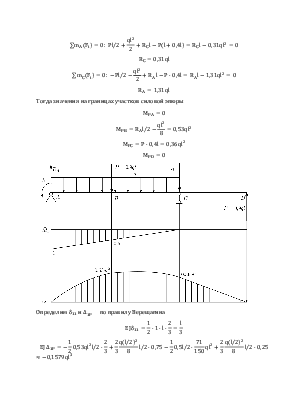
Тогда из канонического уравнения находим момент на левой опоре

Эпюры  и

Для построения суммарных эпюр вычислим реакции в опорах

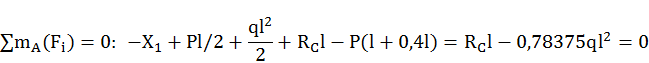
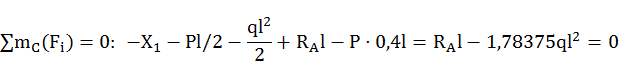
Тогда значения на границах участков эпюр

Эпюра прогибов

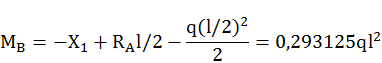
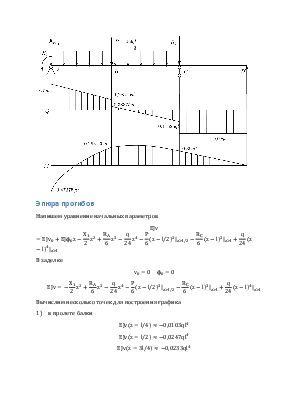
Напишем уравнение начальных параметров

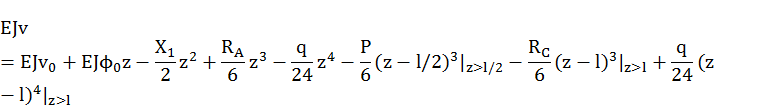
В заделке

Вычислим несколько точек для построения графика

1)  в пролете балки

2)  на консоли