Расчет оборотов двигателя при заданной температуре. Составление плана выпуска трех видов продукции

Министерство образования и науки Российской Федерации

Саратовский государственный технический университет

Кафедра “ЭУН”

КОНТРОЛЬНАЯ  РАБОТА

по дисциплине “Информатика”

за второй семестр 2015 – 2016 учебного года

Выполнила: студент 2 курса

СТЗС11

Проверил: доцент кафедры “ЭУН” к.т.н.

Саратов 2016

Содержание

Задача 1                                                                                                   

Задача 2

Задача 3

Задача 4

Задача 5

Задача 1

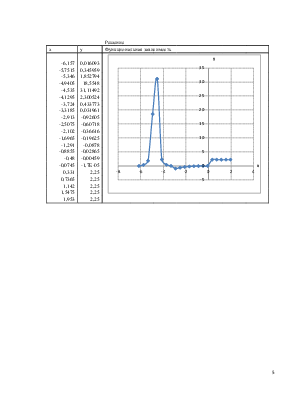
Число оборотов двигателя y функционально зависит от температуры x. Вычислить число оборотов двигателя y(x) при температуре a и b. Построить график этой функциональной зависимости на интервале [a,b] с шагом 0,05l; l – длина отрезка [a,b].

Решение:

1. Укажем диапазон изменения переменной x с помощью арифметической прогрессии с указанным шагом (Правка-Заполнить-Прогрессия).

2. Определим значение функции y(x) с  помощью функции ЕСЛИ.

3. Построим график зависимости y(x) (выделим нужный диапазон построения - Вставка-Диаграмма-Точечная).

3. С помощью контекстного меню внесем изменение в оформление графика.

Задача 2

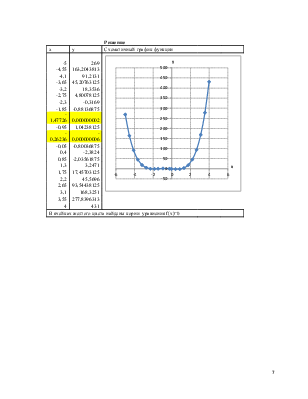
Число оборотов f, как и в предыдущей задаче функционально зависит от температуры x. Требуется найти температуру, при которой число оборотов равно нулю, то есть найти все корни уравнения f(x)=0 на отрезке локализации.

Решение:

1. Укажем диапазон изменения переменной x с помощью арифметической прогрессии с указанным шагом (Правка-Заполнить-Прогрессия).

2. Определим значение функции y(x) с  помощью арифметических функций.

3. Построим график зависимости y(x) (выделим нужный диапазон построения - Вставка-Диаграмма-Точечная).

3. С помощью контекстного меню внесем изменение в оформление графика.

4. Найдем визуально приблизительные корни уравнения, вызовем Подбор параметра и укажем  нужные параметры. В результате подбора  найдем искомые корни уравнения, сделаем заливку желтого цвета в ячейках с найденными значениями.

Задача 3

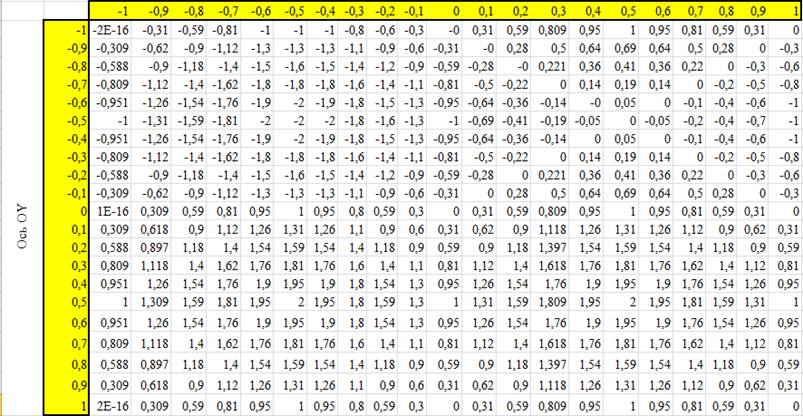
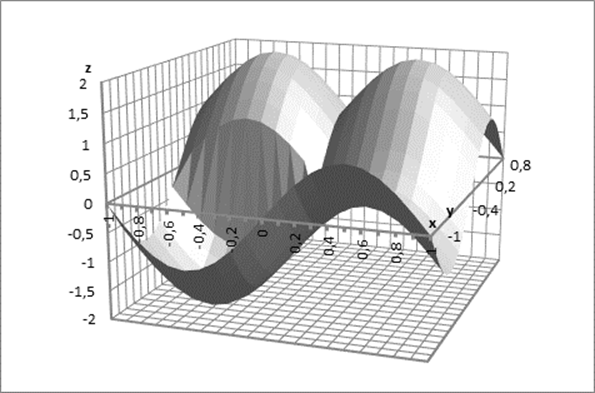
Построить таблицу значений функции z(x,y) и ее отображение в виде поверхности на области  с шагом 0,1 по каждому направлению.

Решение:

1. Заполним диапазоны значений x и y с указанным шагом.

2. Вычислим значение функции z(x,y) с помощью функции ЕСЛИ.

3. Построим поверхность z(x,y)  (выделим нужный диапазон построения - Вставка-Диаграмма-Поверхность).

4. С помощью контекстного меню внесем изменение в оформление графика поверхности.

Задача 4

Организация использует пять складов, на которых находится S1, S2, S3, S4, S5 тонн сырья. Его требуется доставить на 8 предприятий организации. Потребности предприятий в сырье равны P1, P2, P3, P4, P5, P6, P7, P8 соответственно, причем åS_i = åP_j. Стоимость перевозки 1 тонны сырья с i-го склада на j-е предприятие равна A_jⁱ (матрица {A} задана). Средствами поиска решения определить план перевозок, при котором фирма понесет наименьшие издержки по перевозкам, и определить эти издержки.

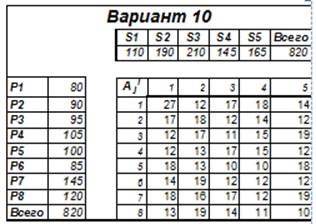
Математическая модель

Решение:

1. Найдем значение в ячейках «Всего» (по складам и предприятиям) (с помощью функции СУММ) и «Всего стоимость» (с помощью функции СУММПОИЗВ.

2.  Найдем значение Общей стоимость перевозок как сумму всех стоимостей по складам.

3. С помощью меню Сервис-поиск решения найдем минимальную стоимость перевозок, предварительно указав все указанные в задании настройки для вычислений и ограничения для расчетов.

Решение в Excel:

Задача 5

Требуется составить план выпуска трех видов продукции П1, П2, П3. Для выпуска каждой единицы каждого вида продукции нужны ресурсы (сырье) четырех видов С1, С2, С3, С4 в количестве a_ij, где i – продукция, j – сырье. Запасы сырья C1, C2, C3, C4 – c1, c2, c3, c4 соответственно. Прибыль от выпуска единицы каждой продукции П1, П2, П3 – р1, р2, р3. Требуется максимизировать прибыль. При этом следует учесть ограничения:

Σa_ij·x_i≤c_j, j=1..4,

где x_i – количество произведенной продукции.

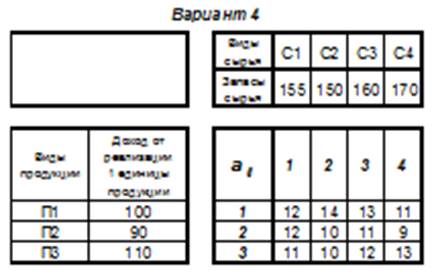
Решение:

1. Вычислим Общий доход как произведение дохода за 1 д. продукции ее на количество по каждому виду продукции.

2. Найдем значение суммарного дохода с помощью функции СУММ.

3. Вычислим Общие затраты (по каждому сырью) как произведение затрат на 1 ед. продукции и количества продукции.

4. Вычислим общие затраты по каждому сырью с помощью функции СУММ