Методические рекомендации по оценке статистических характеристик результатов эксперимента

Ошибки подразделяются на грубые, случайные и систематические.

Примером грубых ошибок может служить, например, неправильное использование шкал при измерении твердости, арифметические ошибки в вычислениях, перепутанные образцы после различной термообработки и т.д. Наличие ошибок проявляется в том, что среди сравнительно близких результатов наблюдается одно или несколько значений, заметно выделяющихся по величине из общего ряда. Если отличие настолько велико, что можно говорить о  грубой ошибке, то это измерение сразу отбрасывают. Однако в большинстве случаев нельзя сразу признать то или иное наблюдение неверным только по признаку «выскакивания» их общего ряда, и нужно провести дополнительные исследования.

К систематическим ошибкам, в первую очередь, относят, так называемые, инструментальные ошибки, которые возникают вследствие ограниченной точности измерительных приборов. Общим признаком систематических ошибок можно считать принципиальную возможность изучить их и исключить из результатов измерений.

Однако следует отметить, что под теорией ошибок обычно подразумевается теория случайных ошибок. Причиной случайных ошибок может быть недостаточно четкое проведение различных операций. Так, многократные измерения одной и той же величины, произведенные с возможной тщательностью, и учет всех систематических ошибок всегда дают различные числовые значения. Случайных причин, вызывающих отклонение от точного значения, много, и они, как правило, не поддаются учету. Каждая из этих причин дает малозаметное отклонение, так как в противном случае оно было бы отличено и изучено. От  случайных ошибок избавиться невозможно. Можно лишь приближенно оценить их влияние на погрешность эксперимента.

Случайные ошибки связаны с несовершенством наших органов чувств, изменением внешних условий (температуры, влажности, давления).

1.1   Математические критерии оценки результатов эксперимента

Случайные ошибки в большинстве случаев подчиняются закону нормального распределения, математическое выражение которого имеет следующий вид:

у = ;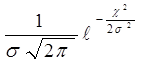

где у – плотность распределения ошибок;

 – основание натуральных логарифмов, равное 2,72;

χ = χ _ί –  – ошибка результата единичного определения;

     – среднее арифметическое из n измерений

χ _ί – результат единичного определения;

σ² – генеральная дисперсия.

Графически закон нормального распределения может быть представлен в виде кривой Гаусса (рисунок 1)

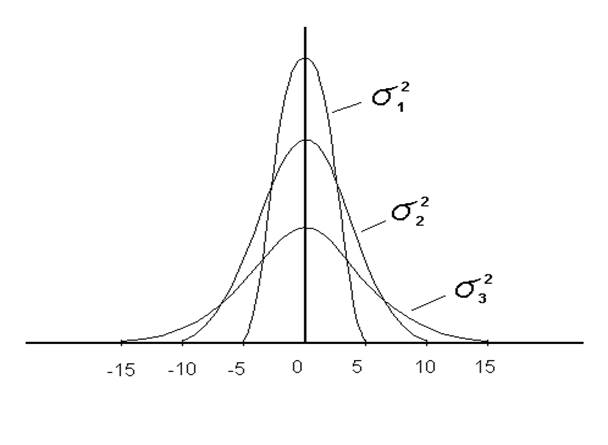
Рисунок 1 – Кривая Гаусса (σ₁ ² < σ₂ ² < σ₃ ²).

Сравнение этих кривых показывает, что с уменьшением величины дисперсии улучшается распределение и уменьшается предел, который практически могут достигнуть ошибки.

Генеральная дисперсия является понятием теоретическим, а на практике обычно имеют дело с выборочной дисперсией, обозначаемой S².

Следовательно, одним из основных метрологических требований к методу анализа является достаточно малая  величина  выборочной  дисперсии или средней квадратичной ошибки отдельного определения, равной .

Обычно величину выборочной дисперсии рассчитывают по формуле:

S² =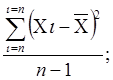

где Х_i – результат единичного определения;

n – число измерений;

К=n-1 – число степеней свободы;

 - среднее арифметическое из n измерений.

Среднее арифметическое измеряют по формуле:

Если разность , то такие результаты опыта отбрасывают.

Следует также иметь в виду, что по закону сложения ошибок средняя квадратичная ошибка суммы независимых величин равна корню квадратичному из суммы дисперсий отдельных слагаемых.

Другим математическим показателем, посредством которого оцениваются полученные результаты опыта, является наряду с дисперсией «доверительный интервал» – интервал, в котором находится истинное значение определяемой величины с заданной доверительной вероятностью. Значение доверительного интервала определяется выражением:

Дробь  обозначают через  и называют квадратичной ошибкой среднего арифметического, а    - абсолютной ошибкой среднего арифметического.

Тогда доверительный интервал выражается формулой:

 или

, где a – истинное значение определяемой величины;

Х – среднее арифметическое из n измерений;

- средняя квадратичная ошибка среднего арифметического;

- критерий Стьюдента;

n – число измерений;

- абсолютная ошибка среднего арифметического.

Вероятность того, что доверительный интервал действительно заключает в себе истинное значение величины "а", называют надежностью доверительного интервала α. Обычно принимают значение, равным 0,95 или 0,99.

Для того чтобы рассчитать доверительный интервал, задаются величиной n (или к=n-1) определяют по таблицам критерий Стьюдента . Величина критерия Стьюдента для значений α, равного 0,95 или 0,99 приведена в таблице 1.

Таблица 1 – Распределение Стьюдента

2 ПРИМЕР СТАТИСТИЧЕСКОЙ ОБРАБОТКИ

ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

При определении содержания продуктов коррозии весовым методом было получено десять значений искомой величины (таблица 2). Определить абсолютную и относительную ошибку результатов анализа