Задачи линейного программирования (Приложение к лабораторным работам по курсу "Промышленная логистика")

Приложение 1 к лабораторным работам по курсу “ Промышленная логистика”

         1. 1. Задачи линейного программирования

1.1.1. Пример постановки задачи линейного программирования

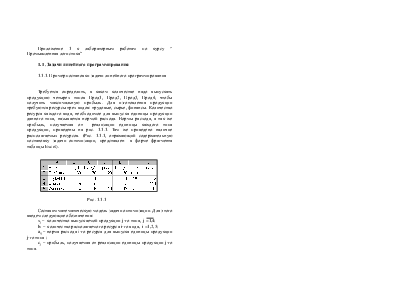
Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, чтобы получить максимальную прибыль. Для изготовления продукции требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а так же прибыль, получаемая от  реализации единицы каждого типа продукции, приведены на рис. 1.1.1. Там же приведено наличие располагаемых ресурсов. (Рис. 1.1.1, отражающий содержательную постановку задачи оптимизации, представлен  в форме фрагмента таблицы Excel).

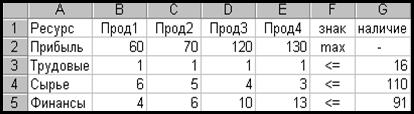Рис. 1.1.1

Составим математическую модель задачи оптимизации. Для этого введем следующие обозначения:                                                                         

         x_j  –  количество выпускаемой продукции j-го типа,  j =1,4;

b_i  –  количество располагаемого ресурса i-го вида,  i =1,2,3;

a_ij – норма расхода i-го ресурса для выпуска единицы продукции j-го типа ;

c_j  – прибыль, получаемая от реализации единицы продукции j-го типа.

Сформируем целевую функцию, отражающую прибыль, получаемую от всех видов продукции. Очевидно, что эту функцию следует  максимизировать.

Сформируем далее ограничения. Как видно из рис. 1.1.1, для выпуска единицы продукции Прод1 требуется 6 единиц сырья. Следовательно, для выпуска всей продукции Прод1 требуется 6x₁ единиц сырья, где x₁ – количество выпускаемой продукции Прод1. С учетом того, что для других видов продукции зависимости аналогичны, ограничение на использование сырья будет иметь вид:

6x₁+5x₂+4x₃+3x₄ £ 110 .

Аналогично можно составить ограничения для остальных ресурсов. Тогда математическая модель задачи оптимизации будет иметь вид:                                                    

                            z = 60x₁ +70x₂ + 120x₃ +130 x₄ ® max

x₁ + x₂  + x₃  + x₄   £ 16                                 

6x₁ +5x₂ + 4x₃ +3x₄  £ 110                                      (1.1.1)                         

4x₁ +6x₂ + 10x₃ +13x₄  £ 91

x _j ³ 0 ;  j =1, …,4                                     

(Последняя строка математической постановки задачи представляет собой условия  неотрицательности переменных  x_j ).

1. 1. 2. Последовательность решения задачи линейного програм-мирования с помощью Excel

1. 1. 2. 1  Блок-схема решения задачи

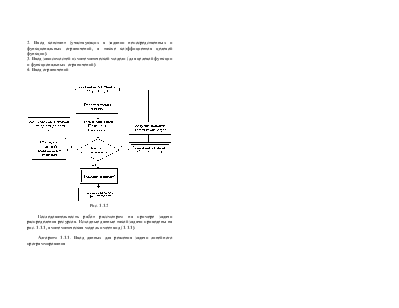
В Excel решение задачи линейного программирования осуществляется симплекс-методом. Последовательность решения такой задачи с помощью Excel приведена на блок-схеме на рис. 1.1.2. Рассмотрим эту последовательность подробнее.

1.1.2.2.   Ввод  условий задачи

Ввод  условий задачи состоит из следующих основных шагов:

1. Создание формы для ввода условий задачи.

2. Ввод констант (участвующих в задании непосредственных и функциональных ограничений, а также коэффициентов целевой функции).

3. Ввод зависимостей из математической модели (для целевой функции и функциональных  ограничений).

4. Ввод ограничений

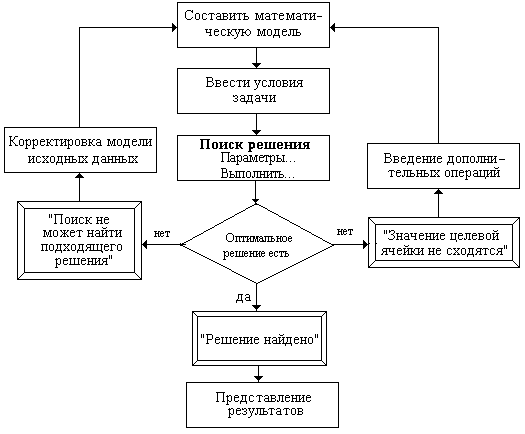Рис. 1.1.2

Последовательность работ рассмотрим на примере задачи распределения ресурсов. Исходные данные такой задачи приведены на рис. 1.1.1, а математическая модель имеет вид (1.1.1).

Алгоритм 1.1.1. Ввод данных для решения задачи линейного программирования

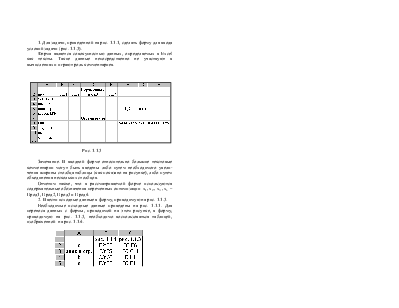
1. Для задачи, приведенной на рис. 1.1.1, сделать форму для ввода условий задачи (рис. 1.1.3).

Форма является совокупностью данных, определяемых в Excel как тексты. Такие данные непосредственно не участвуют в вычислениях и играют роль комментариев.

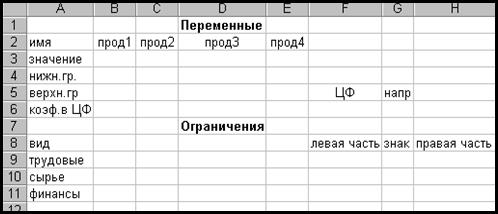Рис. 1.1.3

Замечание. В вводной форме относительно большие текстовые комментарии могут быть введены либо путем необходимого увели-чения ширины столбца таблицы (как показано на рисунке), либо путем объединения нескольких столбцов.

Отметим также, что в рассматриваемой форме используются содержательные обозначения переменных оптимизации  x₁, x₂ ,  x₃ , x₄  – Прод1, Прод2, Прод3 и Прод4.

2.  Ввести исходные данные в форму, приводимую на рис. 1.1.3.  

Необходимые исходные данные приведены на рис. 1.1.1. Для переноса данных с формы, приводимой на этом рисунке, в форму, приводимую на рис. 1.1.3, необходимо воспользоваться таблицей,  изображенной  на рис. 1.1.4.

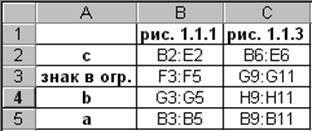Рис. 1.1.4

3.   Ввести зависимости из математической модели (1.1.1).

Для наглядности  можно перейти к режиму представления формул  (см. приложение).

Excel-таблица с введенными  данными приведена на рис. 1.1.5, а та же таблица в режиме представления формул – на рис. 1.1.6.

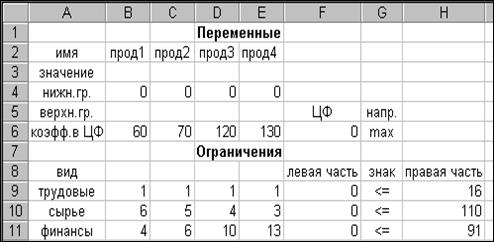Рис. 1.1.5

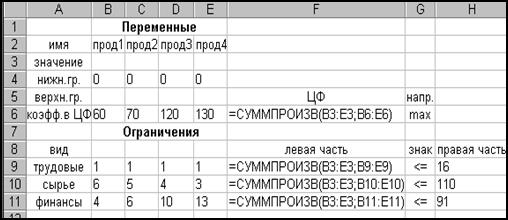Рис. 1.1.6

3.1. Ввести зависимость для целевой функции:

Ø  Курсор в F6.

Ø  Курсор на кнопку  Мастер Функций.

Ø  М1.

На экране: диалоговое окно Мастер функций шаг 1 из 2.

Ø  Курсор в окно Категория на категорию  Математические.

Ø  М1.

Ø  Курсор в окно Функции на СУММПРОИЗВ.

Ø  М1.

Ø  Далее.

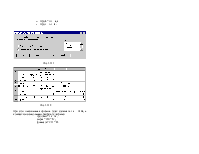
На экране: диалоговое окно (рис. 1.1.7).

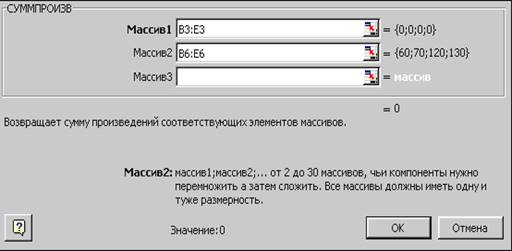Рис. 1.1.7

Ø  В массив 1 ввести B$3:E$3 (адреса ячеек, содержащих пере-менные оптимизации).

Заметим, что: 1) переменные оптимизации первоначально равны нулю, 2) адреса ячеек могут быть введены в диалоговые окна либо с клавиатуры, либо путем “протаскивания” мыши по ячейкам, чьи адреса следует ввести (см. приложение).

Ø  В массив 2 ввести B6:E6 (значения коэффициентов целевой функции