Расчет параметров отдельного фрагмента центра коммутации и его исследование, страница 2

Четвёртая заявка третьего цикла встанет в очередь, и, не дождавшись обслуживания (T_ож = 27 м.е.), уйдёт в отказ (ОТК3). Пятая заявка третьего цикла уйдёт в отказ по входу (ОТК1). Шестая, седьмая и восьмая заявки третьего цикла последуют примеру четвёртой заявки третьего цикла. Девятая заявка третьего цикла уйдёт в отказ из-за отсутствия свободных мест в очереди и приборе обслуживания (ОТК2). Первая, вторая и третья заявки четвёртого цикла уйдут в отказ по входу (ОТК1).

Четвёртая, пятая, шестая и седьмая заявки четвёртого цикла друг за другом будут поступать в очередь и через 3 м.е. переходить на освободившееся место в обслуживающем приборе (в моменты времени 158, 163, 168 и 173 м.е. соответственно).

Восьмая и девятая заявки четвёртого цикла встанут в очередь на ожидание обслуживания.

Таким образом, за время моделирования при предложенных исходных данных зафиксировано 18 отказов, из них:

– 1 рода – 11 отказов;

– 2 рода – 2 отказа;

– 3 рода – 5 отказов.

На рисунке 2 приведены временные диаграммы функционирования модели на протяжении T = 185 м.е.

 

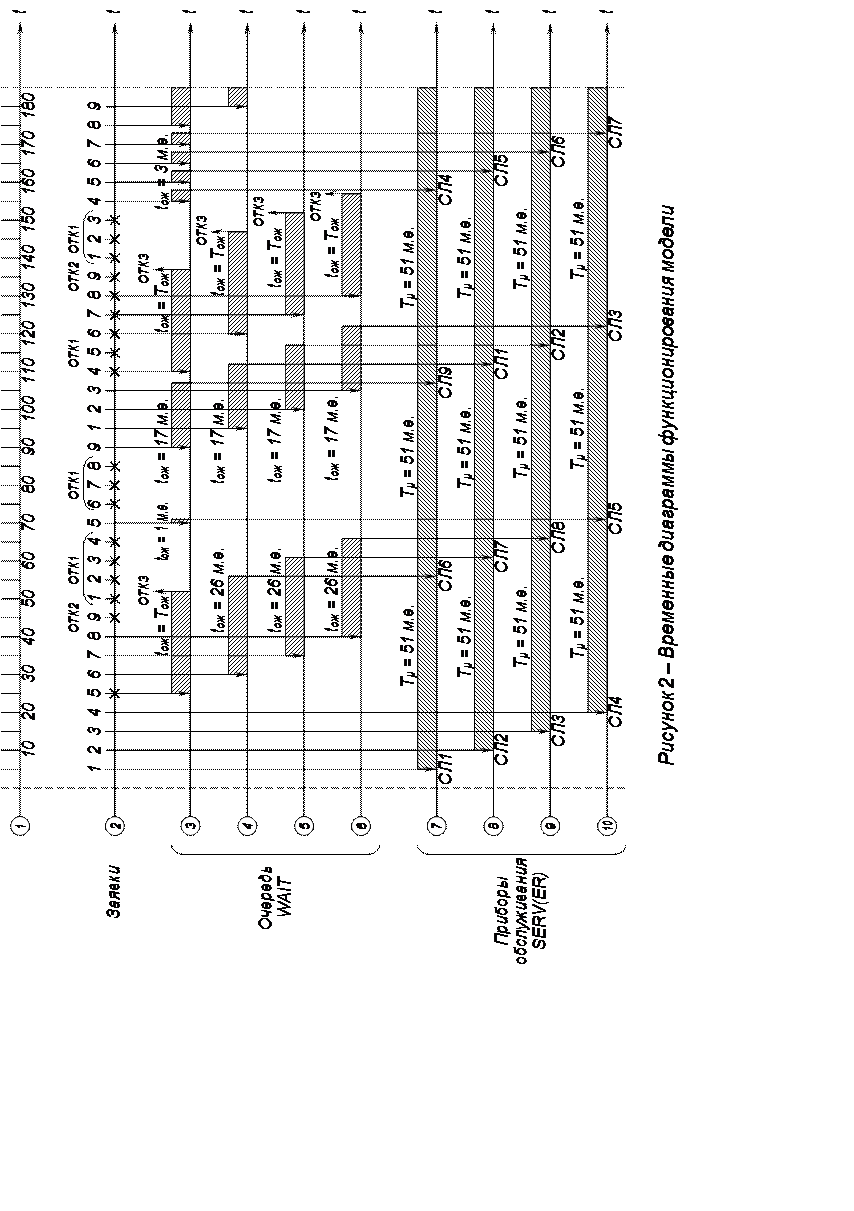2      Таблица функционирования модели

Таблица 2 – Таблица функционирования модели в течение 185 м.е.

№ заявки	№ соединительной линии	№ позиции в очереди	№ метса обслуживающего прибора	№ отказа
1	1	–	1	–
2	2	–	2	–
3	3	–	3	–
4	4	–	4	–
5	5	1	–	3
6	6	2	1	–
7	7	3	2	–
8	8	4	3	–
9	9	–	–	2
10	1	–	–	1
11	2	–	–	1
12	3	–	–	1
13	4	–	–	1
14	5	1	4	–
15	6	–	–	1
16	7	–	–	1
17	8	–	–	1
18	9	1	1	–
19	1	2	2	–
20	2	3	3	–
21	3	4	4	–
22	4	1	–	3
23	5	–	–	1
24	6	2	–	3
25	7	3	–	3
26	8	4	–	3
27	9	–	–	2
28	1	–	–	1
29	2	–	–	1
30	3	–	–	1
31	4	1	1	–
32	5	1	2	–
33	6	1	3	–
34	7	1	4	–
35	8	1
36	9	2

3.     Расчёт параметров

Среднее время занятия СЛ определим по формуле:

                                                                                       [ 1 ]

где    – время занятия СЛ индивидуальным вызовом;

         – число занятий СЛ.

Вероятность отказов вычислим по формуле:

                                                                        [ 2 ]

где    – число отказов соответствующего типа;

         – общее число заявок.

        ЛИТЕРАТУРА

1      А. В. Буданов, Н. В. Гольцова. «Компьютерные сети: методическое пособие по курсовому проектированию». СПбГУТ. – СПб, 2000