Другие предметы \ Гидравлика

Расчет плотности смеси двух углеводородных жидкостей. Измерение наименьшего перепада давления, страница 4

Q = μ∙ω∙, где μ – коэффициент расхода;

ω – площадь отверстия, м2;

Н – геометрический напор над центром тяжести отверстия.

Т. е. расход жидкости из открытого резервуара не зависит от давления на поверхности бака.

Ответ: расход не изменится.

Вопрос. Сравните расходы при истечении жидкости из бака через отверстие в тонкой стенке и через цилиндрический насадок при одинаковых напорах истечения Но и одинаковых выходных диаметрах.

Решение

Расход жидкости из отверстия определяется по формуле

Q = μ∙ω, где μ – коэффициент расхода;

ω – площадь сечения отверстия, м2;

Н – напор истечения, м.

Площадь сечения и напор истечения одинаковы, т. е. производительность зависит только от коэффициента расхода. По литературным данным коэффициент расхода для отверстия в тонкой стенке μт.с. = 0,6; коэффициент расхода для цилиндрического насадка μцил = 0,82.

Определяем отношение

Qцил;Qт.с. = 0,82:0,6 = 1,37.

Ответ: Qцил;Qт.с. = 1,37.

Вопрос. Три открытых цилиндрических резервуара с одинаковыми сливными насадками на дне заполнены до уровня Н: первый водой, второй нефтью, третий наполовину водой, наполовину нефтью. Сравнить начальные скорости истечения.

Решение

Скорость истечения жидкости из открытого резервуара определяется по формуле, м/с

V = φ.

Вода и нефть отличаются плотностью, а плотность в формуле отсутствует, значит,  скорости истечения одинаковы

Ответ: V1 = V2 =V3.

Вопрос. Сравнить время опорожнения трех приведенных на рисунке открытых резервуаров. Объемы резервуаров и и начальные уровни одинаковы.

Решение

Время опорожнения резервуара определяется по формуле

Т = , где W – объем резервуара,  для всех трех заданных резервуаров одинаковы;

Q – расход жидкости так же одинаков.

Значит время опорожнения трех резервуаров одинаково.

Ответ: время опорожнения одинаково.

Таблица 10

Вопрос. Расположите в порядке убывания скорости распространения волны гидравлического удара в водопроводах заданных диаметров с одинаковыми толщинами стенок труб, но изготовленных из различных материалов: 1) резина, шланг диаметром d; 2)резина, армированная сталью, шланг диаметром d; 3) сталь, труба диаметром d; 4) сталь, труба диаметром 1,2d.

Решение

Скорость распространения ударной волны в трубопроводе определяется  по формуле Жуковского Н. Е.

С = 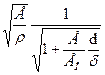, где  Е  – модуль упругости жидкости,  кг/м2;

Ео – модуль упругости материала стенок трубы, кг/м2;

 = 1425м/с - скорость распространения звука в жидкости;

d – диаметр трубы, м;

δ – толщина стенки трубы, м.

Т. е. в нашем случае скорость распространения ударной  волны зависит от модуля упругости материала труб и диаметра труб.

Модули упругости можно принять: для воды – 2030МПа; для резинового шланга – 10МПа; для резины, армированной сталью – 100000МПа; для стальных труб – 200000МПа.

Тогда, скорости распространения ударной волны можно расположит следующим образом: 1, 2, 4, 3.

Ответ: 1, 2, 4, 3.

Вопрос. При постоянном расходе жидкости в трубопроводе его длину, диаметр и толщину стенок уменьшили в 2 раза. Как скажется на ударном повышении давления  при прямом гидравлическом ударе.

Решение

Повышение давления при прямом ударе  определяется по формуле

ΔР = ρСυVo.

Скорость распространения ударной волны в трубопроводе определяется  по формуле Жуковского Н. Е.

Сυ = 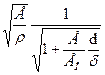, где  d – диаметр трубы, м;

δ – толщина стенки трубы, м.

При уменьшении диаметра трубы и толщины стенки в 2 раза, отношение d/δ не изменится, а значит, ударное повышение давления при прямом гидравлическом ударе не изменится.

Ответ: останется без изменений.

Вопрос. Длину трубопровода от насоса до потребителя пришлось увеличить в 1,2 раза, во сколько же раз уменьшился и расход жидкости. Для перекрытия трубы используется та же концевая задвижка рассчитанная ранее (для первого варианта) на время закрытия при которой ΔР = 0,5ΔРmax. Что произойдет с величиной ΔР в новых условиях?

Решение

Падение давление в задвижке определяется по формуле Мишо

ΔР =, где ρ – плотность жидкости, кг/м3;

ℓ - длина трубопровода до потребителя, м;

υ – скорость движения жидкости, м/с;

τ – время закрытия задвижки, с.

Длина трубопровода ℓ увеличилась, расход жидкости уменьшился, значит, увеличилась скорость υ. Числитель увеличился, ΔР увеличится.

Ответ: увечится.

Список используемой литературы

1. Брыховецкий  О. С. Основы гидравлики. М. Недра. 1991.

2. Рабинович Е. З., Евгеньев А. Е Гидравлика. М. Недра. 1987.

3. Сборник задач по гидравлике. Под редакцией д.т.н профессора Большакова В. А. Киев. «Вищща шола». 1975.

4. Примеры расчетов по гидравлике. Под редакцией Альтшуля А. Д. , М., Стройиздат, 1977.

Скачать файл