Решение задач линейного программирования графическим способом. Составление экономико-математической модели

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего образования

«Национальный исследовательский Томский политехнический Университет»

Институт электронного обучения

080100 «Экономика»

Индивидуальное домашнее задание №1

Вариант - 1

по дисциплине:

Теория экономического анализа

Томск – 2016

Содержание

                                                                                                            С.

Задача 1                                                                                                             3

Задача 24

Задача 36

Задача 47

Список литературы10

Задача 1

Решить графическим способом решения ЗЛП

Имеющиеся ограничения:

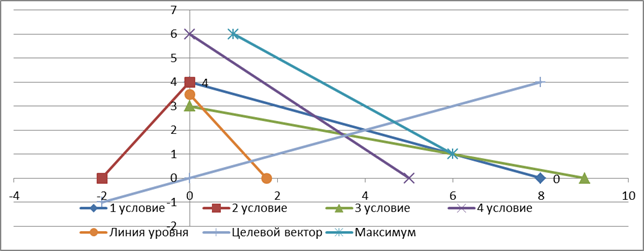
Решим задачу на максимум:

Построим область допустимых решений:

Построим целевой вектор и линию уровня.

Определяем координаты точки, в которой целевая функция достигает максимума при помощи решения системы уравнения:

Задача 2

Составить экономико-математическую модель, далее решить графически

Инвестор, располагающий суммой в 300 тыс. руб., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено по крайней мере в два раза больше, чем акций В, причем последних можно купить не более чем на 100 тыс. руб. Дивиденды по акциям А составляют 8% в год, по акциям В – 10%. Какую максимальную прибыль можно получить в первый год?

1. Составим экономико-математическую модель задачи.

Пусть xi - стоимость акций i-го предприятия, тогда целевая функция задачи линейного программирования будет иметь вид:

Ограничения задачи имеют вид:

 - ограничение по суммарной стоимости акций;

 - ограничение по количеству акций;

 - ограничение на покупку акций В.

По экономическому смыслу задачи

.

Геометрически задача линейного программирования (ЗЛП) представляет собой отыскание такой точки многоугольника допустимых решений (ОДР), координаты которой доставляют целевой функции максимальное значение. Все точки ОДР являются допустимыми. Построим ОДР целевой функции, для чего найдем уравнения ограничивающих прямых.

х₁ + х₂ = 300

х₁ = 0; х₂ = 300

х₂ = 0; х₁ = 300

х₂ = х₁

х₁ = 0; х₂ = 0;

х₁ = 200; х₂ = 100

х₂ = 100 горизонталь, параллельная оси Ох

На графике построим эти прямые и выделим ОДР внутренней штриховкой.

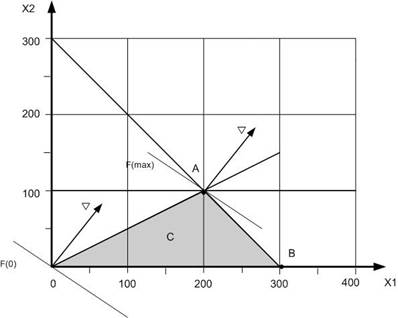
Получили многоугольник ОАВ, угловые точки которого имеют следующие координаты: О(0, 0), A(200; 100); B(300; 0). Координаты вершины А(200, 100) найдены путем подстановки в уравнение 2х₂ = х₁ значения х₂ = 100.

Построим вектор-градиент целевой функции, соединив его вершину (0,08; 0,10) с началом координат О(0, 0) и проведем через начало координат линию уровня целевой функции f(X) = 0 перпендикулярно вектору-градиенту. Смещая эту линию параллельно самой себе вправо-вверх до крайней точки ОДР т.(А), найдем значение целевой функции в этой точке (максимальное):

F(А) = 0,08*200 + 0,1*100 = 26 (тыс.ден.ед.)

Х* = (200, 100)

Таким образом, оптимальный план покупки акций будет следующим: необходимо купить на 200 тыс.руб. акций А и на 100 тыс.руб. акций В, при этом все условия будут выполнены и максимальная прибыль равна 26,0 тыс.ден.ед. При решении данной задачи на минимум оптимальный план был бы равен Xmin = (0, 0) и Fmin = 0, т.е. минимальное значение целевая функция принимает при отсутствии купленных акций, при этом линия уровня целевой функции F(X) касается начальной точки ОДР - точки О(0, 0).

Задача 3

Составить взаимодвойстенную задачу

Имеющиеся ограничения:

Так как исходная задача задана на максимум, ограничения неравенства необходимо привести к виду £ , однако, в данном случае в этом нет необходимости, так как ограничения не содержать уравнений со знаком ≥.

Составим двойственную задачу. В связи с тем, что исходная функция на максимум, двойственная задача на минимум, при этом коэффициенты при переменных в целевой функции соответствуют правым частям ограничений, число переменных равно числу ограничений исходной задачи и равно двум.

Строим ограничения, транспонируя матрицу коэффициентов в ограничениях.

Окончательная двойственная задача будет выглядеть следующим образом:

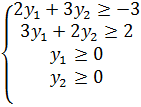
Задача 4

Решить с применением теории межотраслевого баланса

В нижеприведенной таблице приведены данные об исполнении баланса за отчетный период (у.д.е.). вычислить необходимый объем валового выпуска каждой отрасли, если конечный продукт первой отрасли увеличится вдвое, второй отрасли – на 20%, а третьей сохранится на прежнем уровне.

Определим плановые объемы валовой продукции при исходных данных

-  Определим матрицу прямых затрат

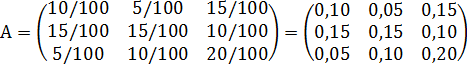
-  Вектор конечного продукта равен

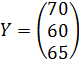
-  Обратная матрица Е к матрице А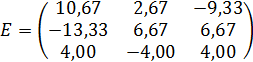  

-  Используем основную формулу межотраслевого баланса

-  Разность матриц Е и А имеет вид

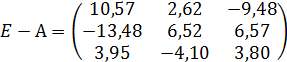
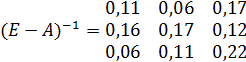
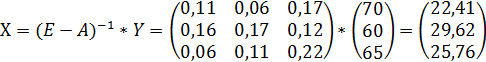
-  Плановый объем валовой продукции отраслей равен:

Продукции 1:     

Продукции 2:     

Продукции 3:     

Перейдем к расчету объемов валовой продукции в случае изменения конечного продукта:

-  Определим матрицу прямых затрат

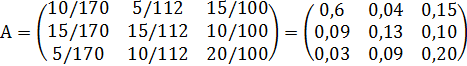
-  Вектор конечного продукта равен

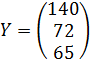
-  Обратная матрица Е к матрице А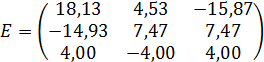  

-  Используем основную формулу межотраслевого баланса

-  Разность матриц Е и А имеет вид

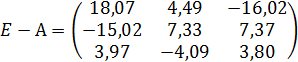
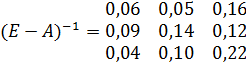
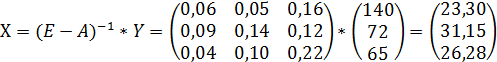
-  Плановый объем валовой продукции отраслей равен:

Продукции 1:     

Продукции 2:     

Продукции 3:     

-  Изменение планового объема валовой продукции отраслей составляет: