Математическая модель процесса лазерного параллельного термораскалывания

Глава 2. Математическая модель процесса лазерного параллельного термораскалывания

Рассмотрим полупространство ζ > О (толстую пластину) нагреваемое лазерным лучом с эллиптическим сечением сильно вытянутым перпендикулярно направлению движения вдоль оси ОХ. Предположим далее, что нагрев осуществляется поверхностным источником бесконечно протяженным в направлении оси 0Υ. Эта модель описывает нагрев сильно поглощающего материала центральной частью протяженного луча лазера и не учитывает краевые эффекты. Однако такое упрощение позволяет решить задачу аналитически и представить решение в наглядном виде. Для учета краевых эффектов надо решать 3D задачу в полном объеме, что потребует больших вычислительных ресурсов.

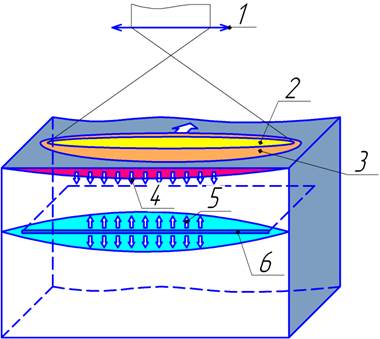
Рисунок 2 – Схема процесса лазерного параллельного термораскалывания.

На рисунке 2: 1 – объектив; 2 – эллиптический пучок излучения лазера на поверхности материала; 3 – область, нагретая движущимся пучком; 4 – напряжения сжатия; 5 – напряжения растяжения в материале; 6 – параллельная трещина.

Будем рассматривать нагрев хрупкого материала, оставаясь тем самым в рамках теории упругости. Квазистатическая задача термоупругости в отсутствие объемных сил заключается в решении уравнений равновесия

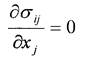
уравнений совместности,

с граничными условиями на поверхности Σ (ζ = 0), которые в отсутствие поверхностных сил имеют вид

где, i и j — принимают значения х, у, ζ и предполагается, что по повторяющимся индексам производится суммирование,

αχ - коэффициент термического расширения, Ε - модуль упругости (модуль Юнга), ν -коэффициент Пуассона, ау - тензор напряжений, T(x,z,t) -распределение температуры в рассматриваемом материале , причем, для задачи упругости время t является параметром, а не переменной.

Для полупространства ζ > 0 в рассматриваемом случае, распределение температуры зависит только от двух пространственных переменных Τ = T(x,z,t). Уравнения совместности запишутся:

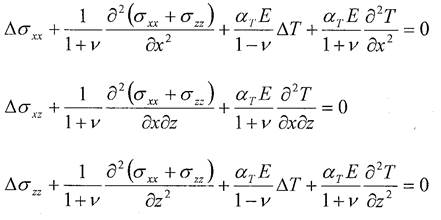
уравнения равновесия

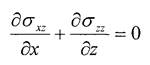
и граничные условия на поверхности ζ = 0 (η = {θ,0,ΐ})

Определим функцию напряжений F(x,z) соотношениями [2]:

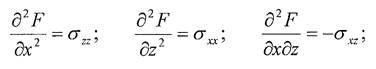
Тогда уравнения равновесия (7,8) удовлетворяются автоматически, а уравнения совместности (4,5,6) сведутся к уравнению

При поверхностном нагреве материала (в отсутствие объемных источников нагрева) частное решение функции напряжений можно определить из уравнения теплопроводности (12) и уравнения совместности (11)

Частное решение функции напряжений определится выражением

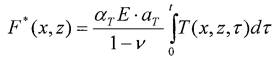
где ат - температуропроводность материала полупространства.

Частное решение для компонент тензора напряжения из (10,13) запишется

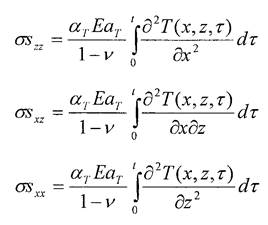
Но решение (14) не удовлетворяет граничным условиям поставленной краевой задачи (9). Поэтому будем искать решение задачи (9) в виде суммы частного решения неоднородного уравнения asy и общего решения однородного уравнения асу (11) с граничными условиями такими, чтобы на поверхности ζ = 0 суммарные нормальные напряжения были нулевыми (см. (9)).

Решение задачи, об упругом полупространстве (ζ > 0), нагруженном на границе силами, зависящими только от переменной х, приведено в [3]. Следует отметить, что при нагреве поверхности полупространства с большим коэффициентом поглощения излучения в материале движущимся лучом лазера, частное решение (14) на поверхности ζ = 0 gsxz(x,0) = 0, так как производная по ζ распределения температуры будет пропорциональна ζ.

Таким образом, на поверхность будет действовать только вертикальная нагрузка, а граничные условия рассматриваемой задачи будут

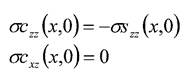
Уравнения равновесия для компонент тензора напряжения асу будут такими же как в (7,8). Уравнение неразрывности (совместности), выраженное в напряжениях запишется [3]

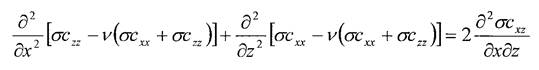
К уравнениям  равновесия и неразрывности (7,8,16) применим преобразование Фурье, определенное соотношениями

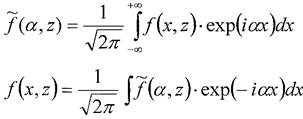
Тогда уравнения равновесия и неразрывности примут вид

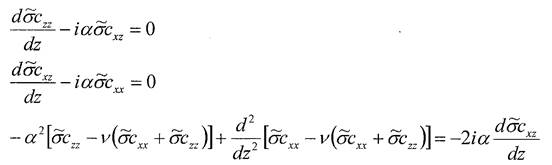
Исключим из этой системы аехх, acxz и получим обыкновенное дифференциальное уравнение

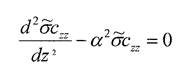
Такие же уравнения получим для асхх, acxz.

К граничному условию (15) применим также преобразование Фурье

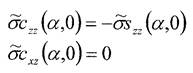
где

Решение уравнения (19) с учетом того, что на бесконечности напряжения стремятся к нулю, будет

где, α > 0 из условия нулевых напряжений на бесконечности. Из первого уравнения (18) определяем acxz

Константы C1 и С2 определяем из граничного условия (20)

Тогда Фурье-образы компонент тензора напряжения выразятся

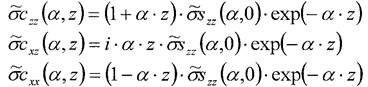
Применим обратное Фурье преобразование к Фурье-образам компонент тензора напряжени (25) и найдем компоненты тензора напряжения, с учетом того, что α > 0 (см. (22))

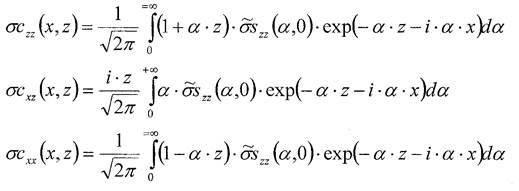
Учитывая, что компоненты тензора напряжения (26) величины действительные запишем

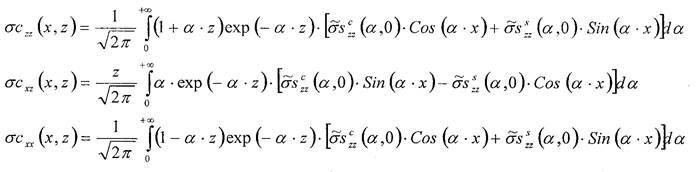
где &sczz и asszz косинус и синус преобразования частного решения соответственно (см. (21)). Значения компонентов тензора напряжений определятся формулами (14) и (27)

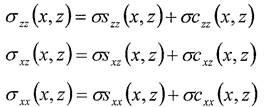
Для примера рассмотрим напряжения, возникающие в толстой пластине (h > 1 мм) из стекла при воздействии на поверхность лазерного луча размером 2а χ 2b, мощностью излучения Ρ и перемещающегося со скоростью ν в направлении оси ОХ.

Параметры стекла λ, с, ρ, Ε, σρ, at - теплопроводность, теплоемкость, плотность, модуль Юнга, коэффициент Пуассона, коэффициент термического расширения соответственно. Линейные размеры в [мм], время в [сек], мощность в [Вт], напряжения в [кГ/мм2] температура в

[°с].

Результаты расчетов приведены на Рис. 1 и Рис. 2. Видно, что на фронте нагрева движущимся поверхностным источником расширяющиеся прогретые участки материала встречают сопротивление окружения и возникают напряжения сжатия (σζ < 0), а в зоне охлаждения поверхностного слоя и растекания тепла вглубь материала ситуация обратная и возникают напряжения растяжения.

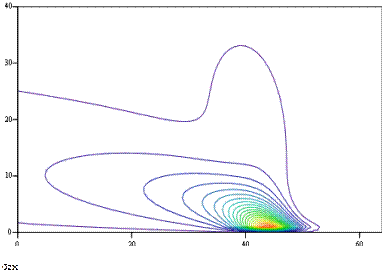
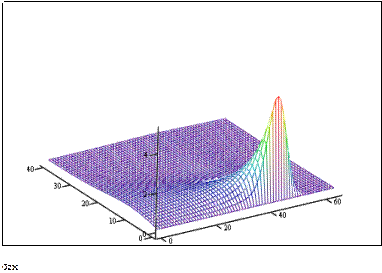
Рисунок 2 - Пространственное распределение  напряжения сдвига s_xz вдоль направления перемещения и  вглубь материала

   

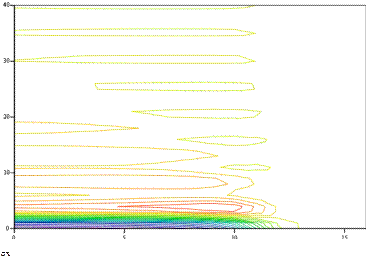
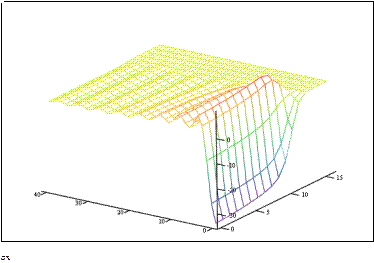
Рисунок 3 - Пространственное распределение  напряжения  s_xx вдоль направления перемещения и  вглубь материала

На самой поверхности напряжения равны нулю, так как поверхность свободная, а максимальные напряжения сосредоточены в приповерхностном слое, куда проникает тепло.

Рисунок 2 – Картина напряжений в материале при лазерном параллельном термораскалывании.

1 – пучок излучения лазера; 2 – объектив; 3 – эллиптический пучок излучения на поверхности материала; 4 – напряжения сжатия; 5, 6 – напряжения растяжения в материале; 7 – параллельная трещина; h – глубина параллельной трещины; V – скорость движения пучка излучения по поверхности материала.

Из Рис. 3 c,d (Зс) - ось ОХ направлена горизонтально, а ось OZ вертикально) видно, что на поверхности полупространства (ζ = 0) напряжение сдвига равно нулю.

В основном это напряжение сосредоточено в приповерхностном слое, максимальное значение приходится на область, где располагается максимум температурного распределения (Рис. 3 а,Ь).

Полученные значения возникающих напряжений не могут расслоить сплошной материал, так как не превышают предела прочности. Но если внутри материала есть трещина, то ситуация меняется, так как вершина исходной трещины является концентратором напряжений и реальные напряжения могут возрасти в десятки раз [5], превышая предел прочности материала. На эксперименте видно, что при наличии внутренней трещины и при этих режимах лазерного нагрева происходит отслаивание слоя стекла толщиной ~ 1мм.

Рисунок 3 – Фотография двух пластин, полученных  методом ЛПТ.