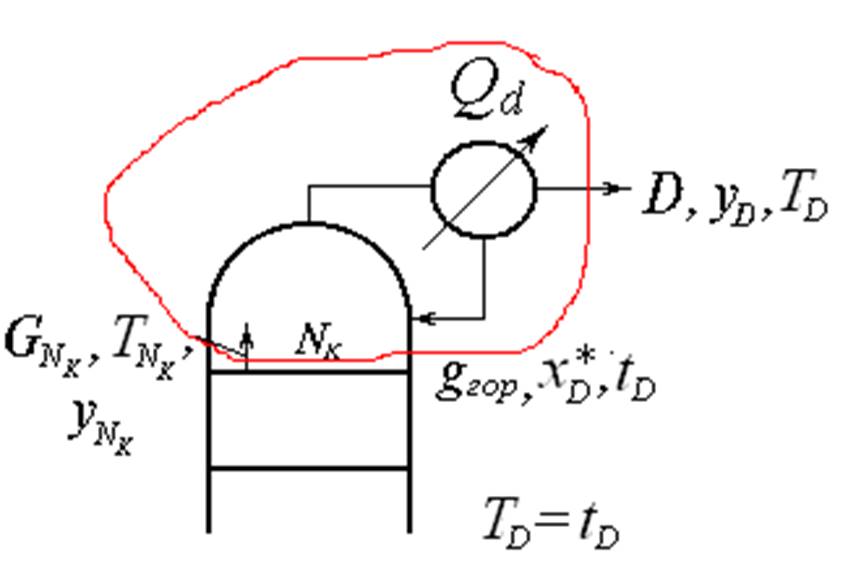
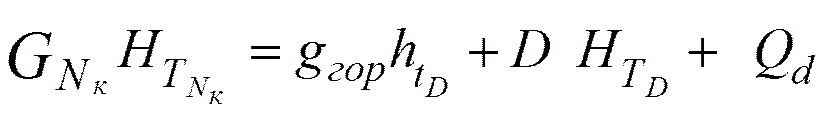
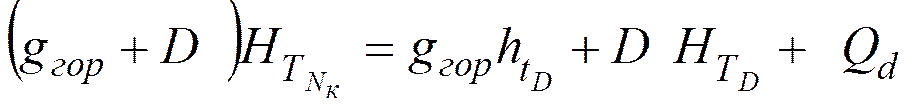
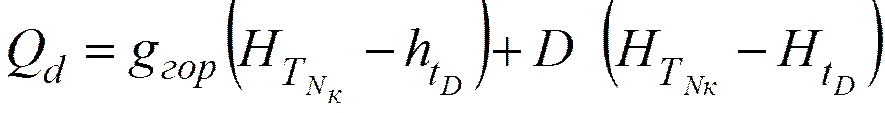
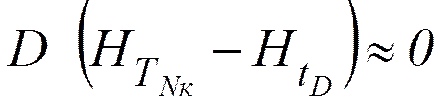
Способы создания орошения в колонне. Парциальный конденсатор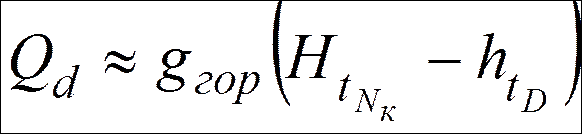. Холодное («острое») испаряющееся орошение

СПОСОБЫ СОЗДАНИЯ ОРОШЕНИЯ

 В КОЛОННЕ

Парциальный конденсатор

         

 .

Холодное  («острое»)

испаряющееся орошение

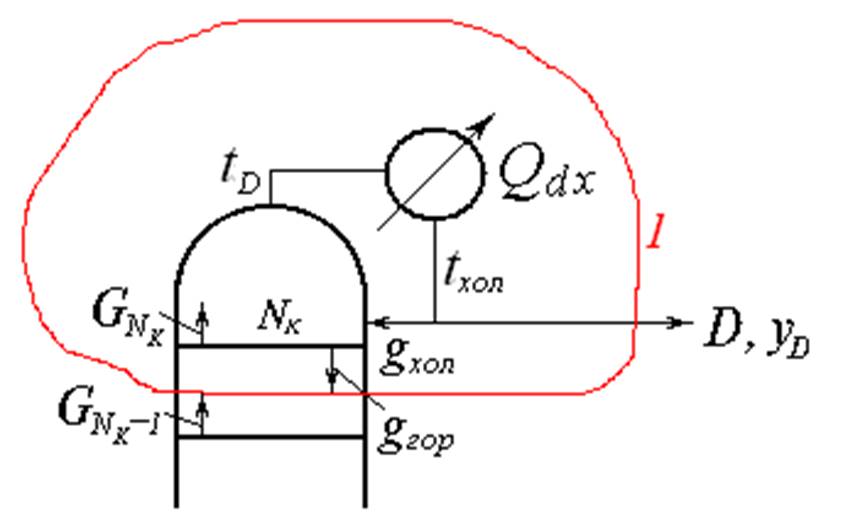
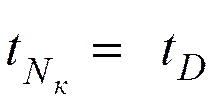
Контур 1

 

 

 

 .

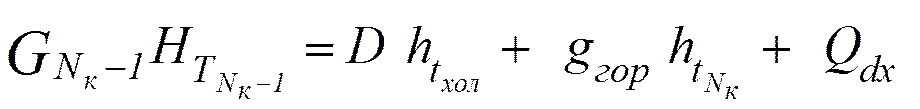
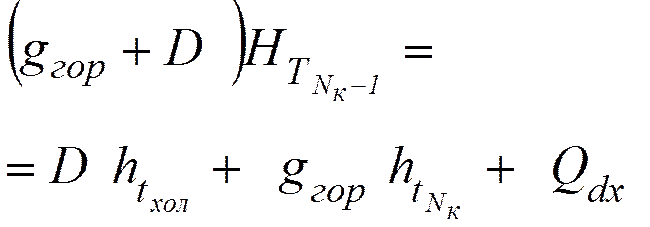
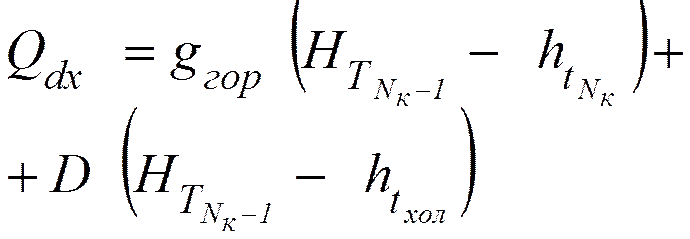
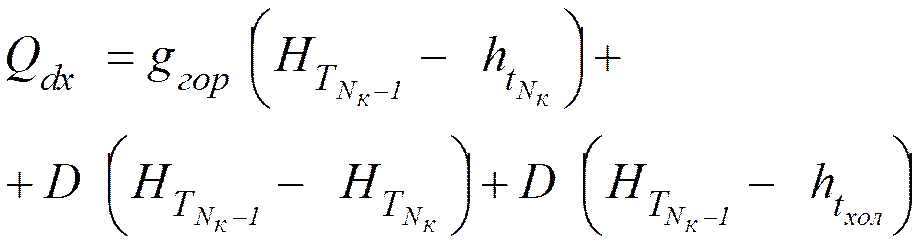
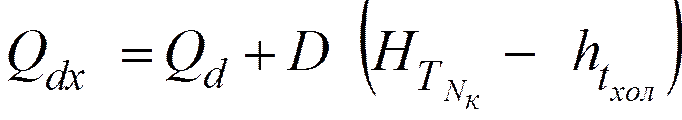Контур 2

 .      

 

 .

 .

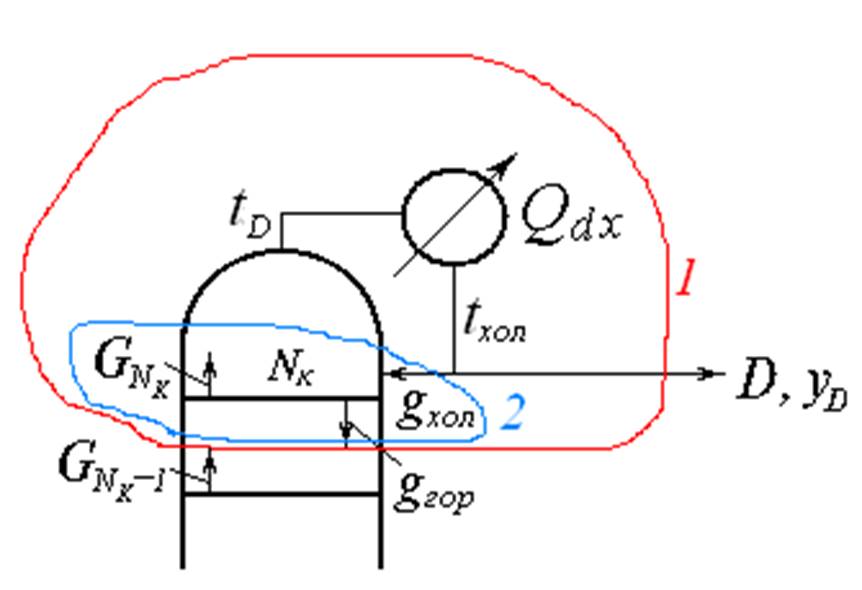
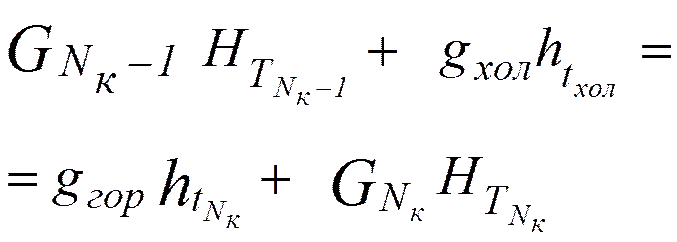
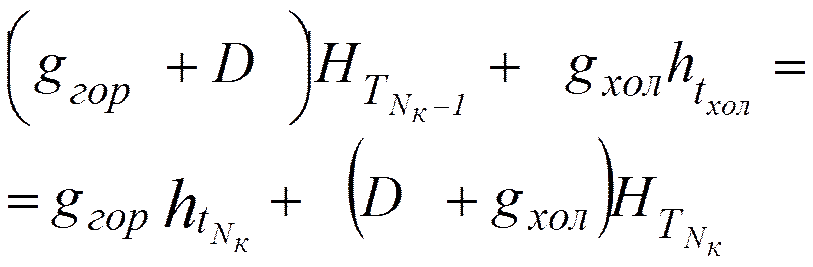
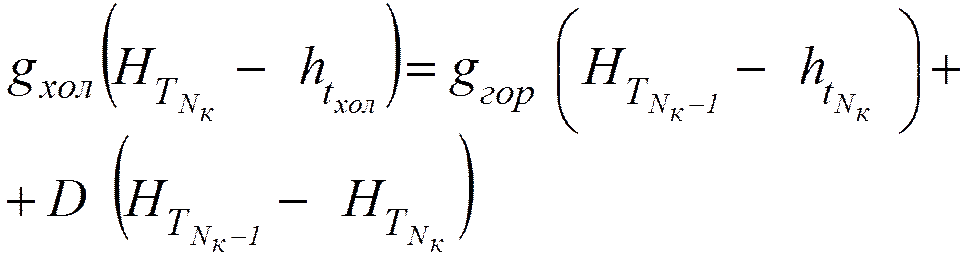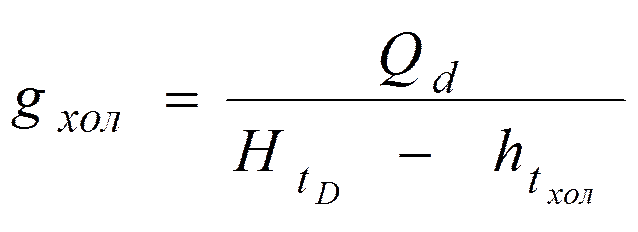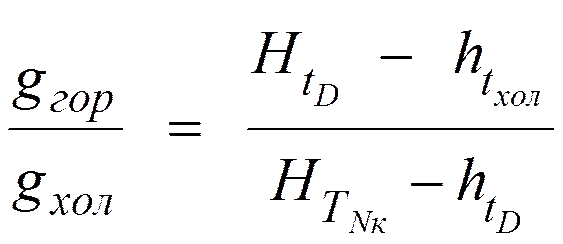Верхнее циркуляционное

 (неиспаряюшееся) орошение

 

 .

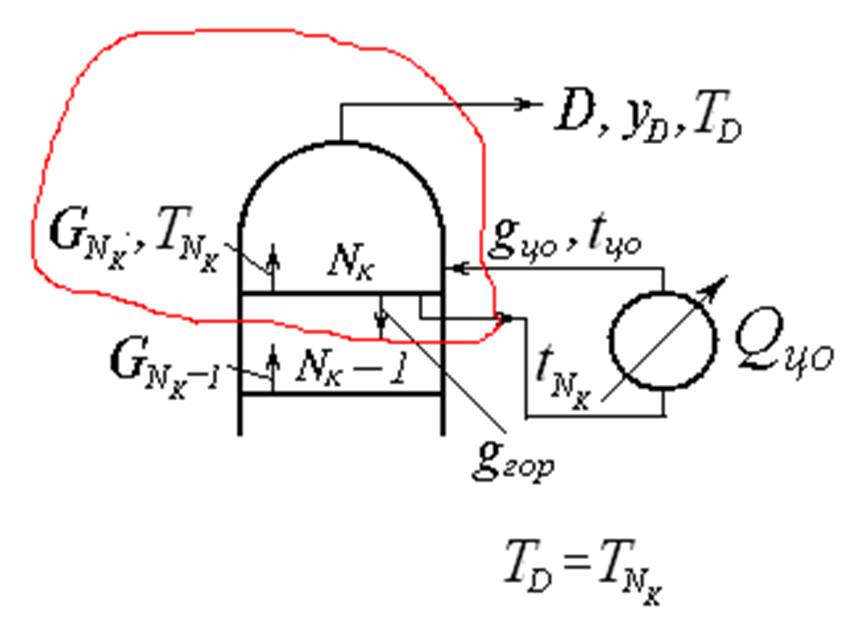
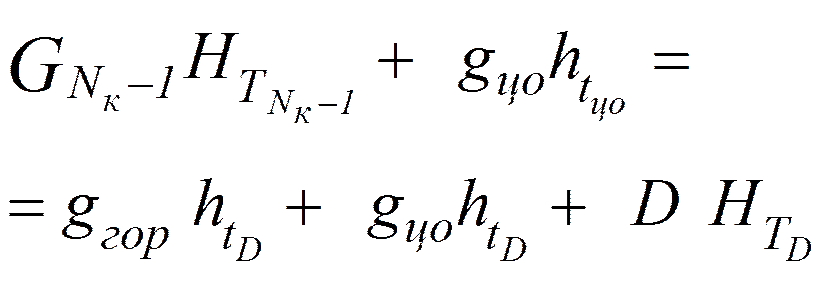
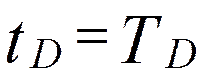
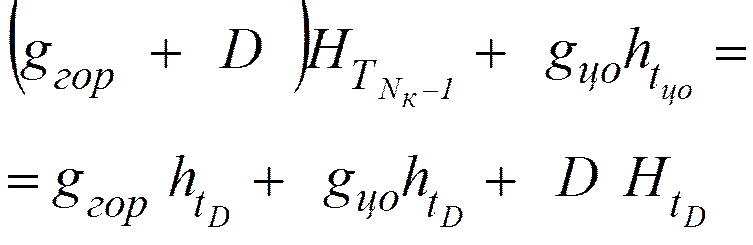
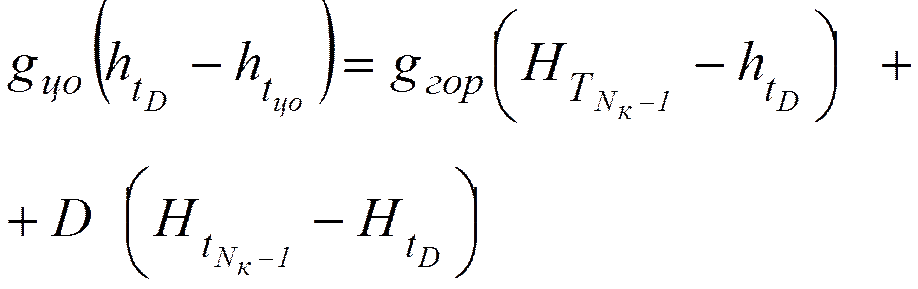
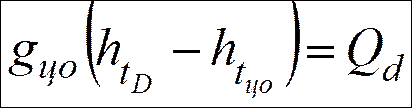
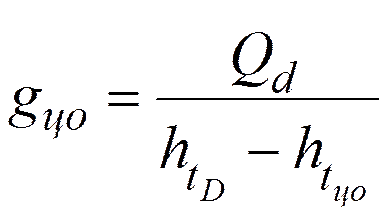
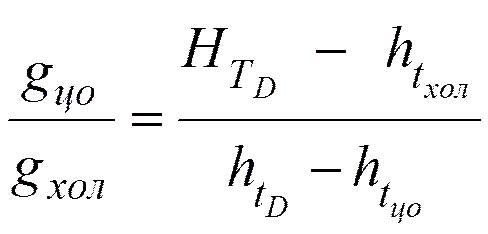СПОСОБЫ ПОДВОДА ТЕПЛА В НИЗ КОЛОННЫ

змеевики или пучки труб, вмонтированные непосредственно в корпус колонны (рис. IV-25, а).

Подогреватель с паровым пространством.

или

 .         (IV, 50)

 .         (IV, 51)

 незначительно отличается от  

 .

          Горячая струя.

 , откуда

 .

Расчет процесса ОИ при вводе циркулирующего потока горячей струи  производится при температуре  и давлении  в нижней части колонны.

Поскольку , то

 .

 ,

 ,

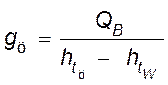ВЛИЯНИЕ ТЕМПЕРАТУРЫ ВВОДИМОГО СЫРЬЯ НА РАБОТУ

РЕКТИФИКАЦИОННОЙ КОЛОННЫ

 .

 ;

 .

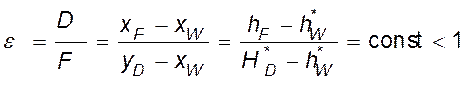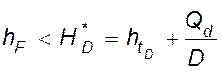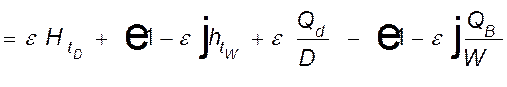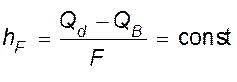 .         (IV, 52)

ВЛИЯНИЕ ДАВЛЕНИЯ НА ПРОЦЕСС РЕКТИФИКАЦИИ

РАСЧЕТ ТЕМПЕРАТУР В РАЗЛИЧНЫХ СЕЧЕНИЯХ КОЛОННЫ

 ,

 ,

 ,

.

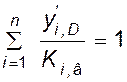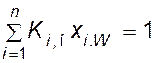 ,         (IV, 53)

.

или

 .

,

 .           (IV, 54)

 .

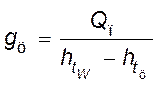ОСОБЕННОСТИ РАБОТЫ РЕКТИФИКАЦИОННОЙ КОЛОННЫ С ВВОДОМ

ВОДЯНОГО ПАРА

 .

 .

 .

 .

 .

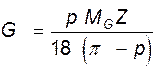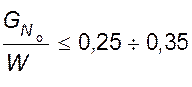
перегретый водяной пар, то

и

 .

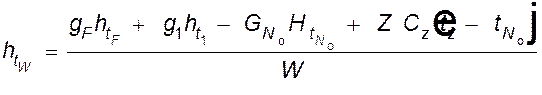1,5 - 3 % массы исходного сырья.

РЕКТИФИКАЦИЯ МНОГОКОМПОНЕНТНЫХ СМЕСЕЙ

Последовательное соединение колонн

Последовательно-параллельяое соединение колонн

С рециркуляцией            

сложные колонны,

ОСОБЕННОСТИ РАСЧЕТА РЕКТИФИКАЦИИ

МНОГОКОМПОНЕНТНЫХ СМЕСЕЙ

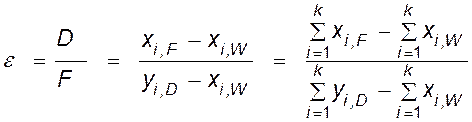          (IV, 55)

и

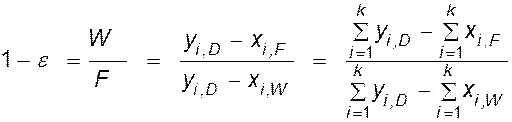 .         (IV, 56)

 .         (IV, 57)

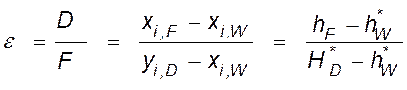          (IV, 58)

и

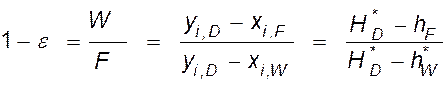 .         (IV, 59)

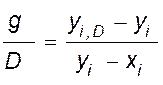          (IV, 60)

 .

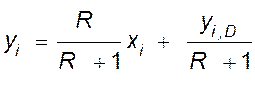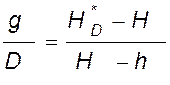 .         (IV, 61)

 .

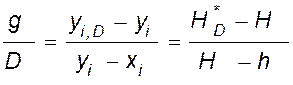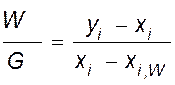          (IV, 62)

 .

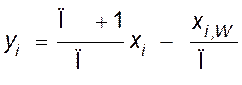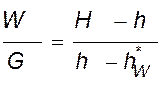 .         (IV, 63)

 .

 .

;                       

;                 .

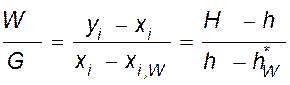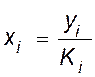
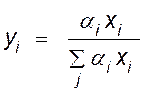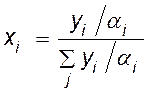1. Заранее нельзя задать составы продуктов колонны,

2. В колонне нет ни одного сечения, в котором составы потоков флегмы и паров совпадали бы полностью с составами жидкости  и паров , полученными при однократном испарении сырья.

3. Поскольку в смеси наряду с НКК и ВКК находятся промежуточные по температурам кипения компоненты,

РАСЧЕТ РЕЖИМА ПОЛНОГО ОРОШЕНИЯ ПРИ

РЕКТИФИКАЦИИ МНОГОКОМПОНЕНТНЫХ СМЕСЕЙ

ПРИБЛИЖЕННЫЙ МЕТОД РАСЧЕТА РЕКТИФИКАЦИИ

МНОГОКОМПОНЕНТНЫХ СМЕСЕЙ ПРИ РАБОЧЕМ

ФЛЕГМОВОМ ЧИСЛЕ

 ,         (IV, 79)

где

 ;                      .

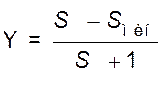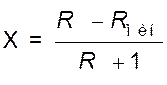и

 .

АНАЛИТИЧЕСКИЙ РАСЧЕТ ЧИСЛА ТАРЕЛОК В КОЛОННЕ

ПРИ РЕКТИФИКАЦИИ МНОГОКОМПОНЕНТНОЙ СМЕСИ

 .

Умножим левую и правую части уравнения рабочей линии на  (где q - пока неизвестный параметр, подлежащий определению) и просуммируем обе части уравнения по всем компонентам:

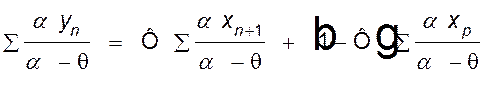 .         (IV, 81)

Выберем параметр q таким образом, чтобы последнее слагаемое обратилось в единицу, т. е.

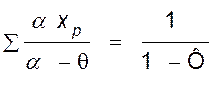 .         (IV, 82)

Уравнение (IV, 82) будет иметь следующий вид для соответствующих частей колонны:

для концентрационной

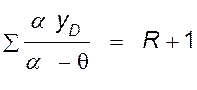 ;         (IV, 83)

для отгонной

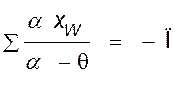 .         (IV, 84)

С учетом уравнения (IV, 82) уравнение (IV, 81) примет вид

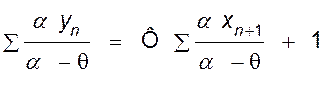 .         (IV, 85)

Перенеся единицу в левую часть уравнения (IV, 81) и приняв во внимание, что , получим

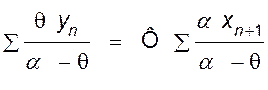 .         (IV, 86)

Параметр q определяется из уравнений (IV, 82) или (IV, 83) и (IV, 84) для соответствующей части колонны. Каждое из этих уравнений имеет столько корней q, сколько компонентов в разделаемой смеси. Для любых двух корней q, например  и , уравнение (IV, 86) можно записать следующим образом:

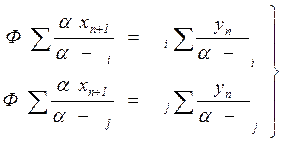 .         (IV, 87)

Разделим правые и левые части приведенных уравнений одну на другую

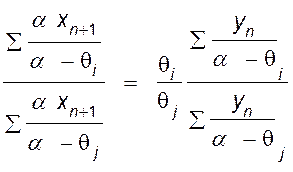 .         (IV, 88)

Чтобы исключить суммы, стоящие в правой части уравнения (IV, 88), выполним соответствующие преобразования уравнения равновесия

 .

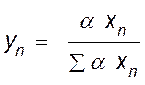Умножим обе части уравнения равновесия на  и произведем суммирование по всем компонентам смеси

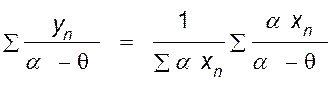 .         (IV, 89)

Выражение  вынесено за знак общей суммы, так как оно не зависит от индекса суммирования (номера компонента).

Для двух корней  и  из уравнения (IV, 89) можем записать

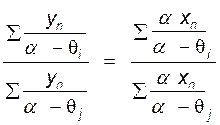 .         (IV, 90)

Из уравнений (IV, 88) и (W, 90) получим соотношение:

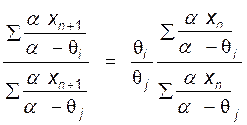 .         (IV, 91)

По виду уравнение (IV, 91) аналогично уравнению (IV, 66), записанному для работы колонны при , в то время как уравнение (IV, 91) справедливо для рабочего флегмового числа, т. е. . Отношение корней / соответствует приведенной относительной летучести  компонентов i и j.

Для упрощения записи последующих уравнений введем функцию

 .

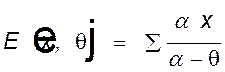Функция  является аналогом концентрации, но не самой концентрацией.

Тогда уравнение (IV, 91) запишется в виде:

 .

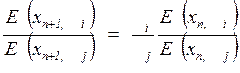Давая n целые значения от 0 до n -1, получим уравнение связи между числом теоретических тарелок и составами в двух произвольных сечениях колонны:

 .

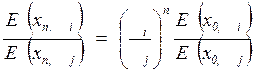Отсюда определяется число теоретических тарелок n между двумя произвольными сечениями колонны (для концентрационной и отгонной частей в отдельности, так как корни q и концентрации различны)

 .

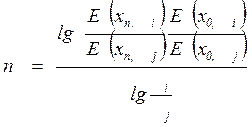Если в качестве одного из сечений, например, с номером ноль, выбрать сечение продуктового потока, то с учетом уравнения (IV, 82) получим

 .

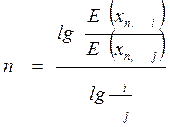С учетом действия кипятильника (или парциального конденсатора) число теоретических тарелок в соответствующей части колонны  определится из уравнения

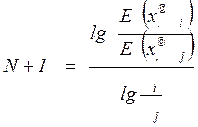 ,         (IV, 91)

где  -концентрация жидкости, стекающей с нижней тарелки верхней части колонны () для концентрационной части колонны, или концентрация жидкости, поступающей на верхнюю тарелку нижней части колонны () для отгонной части колонны.

Уравнение (IV, 91) может быть использовано для расчета числа тарелок в концентрационной  и отгонной  частях колонны. При этом для концентрационной части можно приближенно принять , а для отгонной части , уточняя их последующим расчетом.

В уравнении (IV, 91) влияние состава ректификата или остатка