Наиболее надежный метод определения порядка реакции. Линеаризующие координаты. Отличие временного и концентрационного порядка реакции

??? по Л2

1.  как найти Еа, если нет данных k(Т)                             

2.   наиболее надежный метод определения порядка реакции

3.   что такое линеаризующие координаты

4.  какой фактор наиболее сильно влияет на скорость реакции и почему

5.  в чем отличие временного и концентрационного порядка реакции; возможно ли их равенство

6.  cвязь между теплотой реакции и Е_а

7.  в чем состоит основной подход к составлению кинетической модели

??1-3 по ½ Б; ??4-7 по 1 Б

ЛЕКЦИЯ 3

2. Кинетика сложных реакций

2. 1 Обратимые, параллельные, последовательные и сопряженные реакции

С точки зрения термодинамики в закрытой системе химический процесс может протекать обратимо, до установления состояния равновесия, когда скорости реакции в прямом и обратном направлении равны между собой. Макроскопическая (наблюдаемая) скорость вдали от равновесия равна разности скоростей в прямом и обратном направлении.

Рассмотрим обратимую реакцию 1-го порядка:

k₁

         А Û В   (R4)

k₂

Здесь необходимо учитывать обратную реакцию,   т.е.    r =   r₁- r₂.

Поэтому кинетическое уравнение будет иметь вид:

dC_A/dt = -k₁C_A + k₂C_B                  (27)

Примем для упрощения  C_A= C(0) и C_B = 0, при t=0, тогда это уравнение примет вид:

-dC_A/dt = k₁C_A + k₂ (C(0) –C_A)    (28)

Приведем это уравнение к безразмерному виду (делим на k₂ (C(0)) и разделяем переменные:

-k₂ dt = dα/((1+К)α – 1),  при t=0, α = 1               (29)

Интеграл  (29) имеет вид:

-k₂ t = 1/(1+К) •ln{(1+К)α - 1}                      (30)

Найдем  α (t), преобразовав (30)  и  обозначая (k₁+k₂) = k₁₂

α = 1/(1+К) + К•exp(-k₁₂t)/(1+К)          (31)

поскольку α + β = 1, определим безразмерную концентрацию продукта:

β = К/(1+К) – К•exp(-k₁₂t)/(1+К)         (31а)

Равновесный выход продукта реакции 1^го порядка определяется только константой равновесия

y(B)_eq = β_{tà ∞}  = К/(1+К)              (32)

Таким образом, в случае протекания обратимой реакции типа (R4) можно определить константу равновесия по экспериментальному значению максимального выхода продукта: 

К = β_eq/(1-β_eq)                                      (33)

Рассмотрим описание для бимолекулярной обратимой реакции

k₁

A + BÛD + F    (R5)

 k₂

Снова примем, что C(0)_A= C(0)_B = [A] и С_В=(C(0) –[A]).

Тогда  можно решить уравнение

d[A]/dt = r₁ - r₂ = -k₁[A]² + k₂ (C(0) –[A])² ; t=0, [A]= C(0)      (34)

относительно концентрации А:

[A]

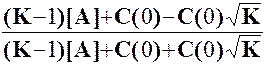2C(0) •k₁t  = -│ln                                                                 C(0)

которое преобразуем к виду:

a = (1+exp(t)/(1++(1-)exp(t ))      (35)

где   exp(t) = exp(-2C(0)k₁t/)   и  K= k₁/k₂

Очевидно, что учет обратимости реакции существенно усложняет вид кинетического уравнения. При сравнении (35) с уравнением (26) для необратимой реакции видно, что для бимолекулярной обратимой реакции концентрацию нельзя выразить в виде явной функции времени реакции.

В  табл. 2 обобщены  интегральные кинетические уравнения и выражения времени полупревращения при протекании реакций различного порядка (m) в газовой фазе, при постоянных T, V, в системе с градиентом концентрации.

Таблица 2. Решения кинетических уравнений различных порядков (m= 0-2))

Кинетическое уравнение (модель) -dCА/dt = k• F(Ci )	Размерность ki	t0,5	a(t)          {a= 1-х}
k (m=0)	моль/(л.с)	0,5C(0) / k	1 - a = kt/C(0)
k[A]0.5 (m=0,5)	(моль/л)0.5с-1	(2- )/ k	1 - a0.5 = kt/2
k[A] (m=1)	с-1	ln2/k	-lna = kt
k[A]2 (m=2)	(л/моль.с)	1/ kC(0)	a = 1/(1+ kC(0)t)
k1[A] - k2[B] (m=1, обр.) (k1+k2) = k12	с-1	ln[2К/(K-1)] k12	α = 1/(1+К) + К•exp(-k12t )/(1+К)           y/y∞ = 1- exp(-k12t );  y∞ = К/(1+К)
k1[A]2 - k2[D]2 [D]=[A]0 - [A] (m=2, обр.)	(л/моль.с)	t0,5 – неявная функция C(0) , k, K и a0,5	a = {1+exp(t)/(1++(1-)exp(t )} exp(t) = exp(-2C(0)k1t/)
A à B à D k1     k2 d[В]/dt= k1[A] - k2[B]	с-1	tmax = k1 ln ρ /(ρ-1)	yBm= ρ 1/(1- ρ)   ;  k1/k2 = ρ ≠ 1

Как видно из табл. 2, зависимость t_0,5 от начальной концентрации закономерно изменяется с увеличением порядка реакции. Так, при m=0 величина t_0,5 пропорциональна C(0), при m=0,5 t_0,5 пропорциональна , при m=1 t_0,5 не зависит от концентрации как для необратимых, так и для обратимых реакций, и при m=2 t_0,5 обратно пропорциональна C(0). Общая формула связи t_0,5, m и C(0) имеет вид:

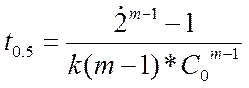       (36)

Заметим, что для реакций 1-го порядка величины a(t) иt_0,5 не зависят от начальной концентрации C(0)!

Найденное аналитическое выражение:

a = (1+exp(t)/(1++(1-)exp(t ))     (35) позволяет решить прямую задачу, т.е. построить кинетические кривые, например, для  k₂= 0,1 (M•c)^-1 при значениях К = 4 - 1000 (рис. 9).

СА   C(0)                            1 2           3         4 t

Рис. 10. Кинетические кривые для реакции 5 при k2= 0,1 (M•c)-1 и К = 4 (1), К= 16 (2): К = 25 (3), К= 1000 (4).

С увеличением константы k₁ равновесие достигается быстрее; однако положение равновесия определяется значением К.

Рассмотрим теперь параллельные реакции, когда реагент одновременно превращается, по двум направлениям (или более)

k₁              k₂

A ® B  и  A ® D              (R5)

Такие реакции весьма распространены, например, при окислении органических веществ параллельно протекают как парциальное (желательное) окисление, так и полное – до СО₂ и воды. Для схемы (R5) кинетика каждой реакции 1) и 2) описывается уравнением 1-го порядка, а убыль концентрации А и селективность по веществу В определяются уравнениями

[A] = C₀exp{-(k₁ +k₂)}t;             (37)  и

S_B = [B]/[B]+[D] = k₁/(k₁ +k₂)      (38)

Заметим, что для этой схемы селективность не является функцией времени и концентрации, а зависит только от соотношения констант скорости. Это, можно сказать, визитная карточка параллельной схемы превращения.

Частным случаем параллельных реакций являются сопряженные реакции, которые могут протекать только совместно, например, окисление сухого СО протекает очень медленно, а при наличии влаги или добавки Н₂ –быстро:

О₂ + СО  à CO₂        ; О₂ + H₂ à H₂O               (R6)

Вещество, инициирующее реакцию (Н₂), называется индуктором; вещество, реагирующее в обеих реакциях, О₂, – называется  актором; вещество, реагирующее только в присутствии индуктора, называется акцептором (СО).

В общем виде можно записать систему:

k₁                                    k₂

А + В (акц.) à D   и  А + I (инд.) à F    (R7)

Для этой схемы на основании 1-го постулата кинетики можно записать:

r_B = k₁ C_AC_B    r_I = k₂ C_AC_I         (39)

Отношение скоростей сопряженных реакций называется фактором индукции