|
Российский государственный университет нефти и газа им. И.М.ГубкинА КАфедра технической механики |
|
Расчётно-графическая работа по курсу «Детали машин» |
|
Расчёт цилиндрического одноступенчатого косозубого редуктора закрытого типа |
|
Выполнил: , студент группы ХТ-06-2 |
|
Проверила: , доцент |
|
Москва, 2007 г. |
Глава 1. Кинематический расчёт привода
§ 1.1. Выбор электродвигателя
КПД привода
![]() , где
, где
![]() - КПД редуктора,
- КПД редуктора,
![]()
![]() - КПД
открытой передачи (зубчатой конической),
- КПД
открытой передачи (зубчатой конической), ![]()
![]() - КПД пары
подшипников,
- КПД пары
подшипников, ![]()
![]() - КПД муфты,
- КПД муфты, ![]() ([1], табл. 1.1)
([1], табл. 1.1)
![]()
Мощность электродвигателя
Требуемая мощность
![]() , где
, где
![]() - мощность
исполнительного механизма,
- мощность
исполнительного механизма, ![]()
![]() - лежит между
стандартными значениями
- лежит между
стандартными значениями ![]() и
и
![]() ([1], табл. П1)
([1], табл. П1)
Проценты перегрузки и недогрузки
![]() , поэтому
, поэтому ![]()
![]()
Число оборотов на валу электродвигателя
Частота вращения вала исполнительного механизма
![]() , где
, где
![]() - угловая
скорость вала исполнительного механизма;
- угловая
скорость вала исполнительного механизма;![]()
![]()
Предварительное число оборотов на валу электродвигателя
![]() , где
, где
![]() - передаточное
число редуктора;
- передаточное
число редуктора; ![]()
![]() -
передаточное число открытой передачи (зубчатой конической);
-
передаточное число открытой передачи (зубчатой конической); ![]() ([1], табл.1.2)
([1], табл.1.2)
![]()
Выбираем стандартное
значение ![]() ([1], табл.П1)
([1], табл.П1)
Выбираем электродвигатель , соответствующий вычисленным числу оборотов и мощности – электродвигатель 80B4. Фактическая частота вращения его вала равна:
![]() ([1], табл.П1)
([1], табл.П1)
§ 1.2.Определение передаточных чисел передач, входящих в состав привода
Общее передаточное число привода
![]() , где
, где
![]() - фактическая
частота вращения вала электродвигателя;
- фактическая
частота вращения вала электродвигателя; ![]()
![]() - частота
вращения вала исполнительного механизма;
- частота
вращения вала исполнительного механизма; ![]()
Передаточное число редуктора
![]() -
предварительное передаточное число редуктора
-
предварительное передаточное число редуктора
Выбираем стандартное
значение: ![]() ([1], стр.10)
([1], стр.10)
Передаточное число открытой передачи
![]()
§ 1.3.Определение частоты вращения, угловой скорости, мощности и крутящего момента на валах привода
Частота вращения
![]()
![]()
![]()
Угловая скорость
![]()
![]()
![]()
Мощность
![]()
![]()
![]()
![]() ;
;
Крутящий момент
![]()
![]()
![]()
Таблица результатов кинематического расчёта привода
|
Вал |
|
|
|
|
Примечание |
|
1 |
1,2 |
1415 |
148,10 |
8,103 |
Вал шестерни |
|
2 |
1,129 |
449,21 |
47,02 |
24,011 |
Вал колеса |
|
3 |
1,05 |
143,01 |
14,97 |
70,140 |
Вал исполнительного механизма |
|
|
|||||
Глава 2. Расчёт зубчатых передач
§ 2.1. Выбор материала шестерни и колеса
Для шестерни и колеса выбираем сталь 45 – углеродистую, качественную, конструкционную сталь, содержащую 0.45 % углерода.
Термообработка: улучшение.
Твёрдость шестерни – ![]() ; Твёрдость
колеса –
; Твёрдость
колеса – ![]() ([1], табл.2.1).
([1], табл.2.1).
§ 2.2. Определение допускаемого напряжения при расчёте на контактную выносливость
![]() , где
, где
![]() - предел
контактной выносливости
- предел
контактной выносливости
![]() - для улучшения
- для улучшения
![]()
![]()
![]() -
коэффициент безопасности,
-
коэффициент безопасности, ![]() -
для улучшения ([1], табл. 2.2)
-
для улучшения ([1], табл. 2.2)
![]() - коэффициент
долговечности,
- коэффициент
долговечности, ![]()
![]()
![]()
Расчётное
напряжение: ![]()
![]()
§ 2.3. Определение допускаемого напряжения изгиба при расчёте на усталость
![]() , где
, где
![]() - предел
выносливости по напряжениям изгиба
- предел
выносливости по напряжениям изгиба
![]()
![]()
![]()
![]() -
коэффициент безопасности;
-
коэффициент безопасности; ![]() -
для улучшения ([1], табл. 2.3)
-
для улучшения ([1], табл. 2.3)
![]() -
коэффициент, учитывающий влияние двухстороннего приложения нагрузки;
-
коэффициент, учитывающий влияние двухстороннего приложения нагрузки; ![]() - при
односторонней нагрузке
- при
односторонней нагрузке
![]() -
коэффициент долговечности;
-
коэффициент долговечности; ![]()
![]()
![]()
§ 2.4. Определение межосевого расстояния
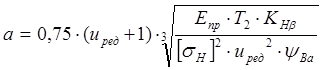 , где
, где
![]() -
приведённый модуль упругости материала колёс;
-
приведённый модуль упругости материала колёс;![]() (шестерня и
колесо – стальные)
(шестерня и
колесо – стальные)
![]() -
крутящий момент на валу колеса;
-
крутящий момент на валу колеса; ![]()
![]() -
допускаемое контактное напряжение;
-
допускаемое контактное напряжение; ![]()
![]() -
передаточное число редуктора;
-
передаточное число редуктора; ![]()
![]() -
коэффициент ширины колеса;
-
коэффициент ширины колеса; ![]()
![]() -
коэффициент концентрации нагрузки по длине зуба.
-
коэффициент концентрации нагрузки по длине зуба.
Выбирается в зависимости от относительной ширины колеса ![]()
![]()
![]()
Выбираем
стандартное значение ([1], табл. 2.4) ![]() и
и ![]() (при твёрдости
рабочих поверхностей зубьев
(при твёрдости
рабочих поверхностей зубьев ![]()
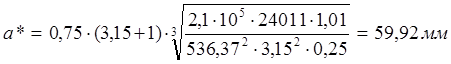
Выбираем
стандартное значение ([1], стр. 20) ![]()
§ 2.5. Определение модуля зацепления
![]()
![]()
Среднее значение модуля зацепления
![]()
Выбираем
стандартное значение (ГОСТ 9563-60) ![]()
§ 2.6. Определение числа зубьев шестерни и колеса
Число зубьев шестерни
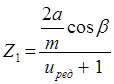 , где
, где
![]() - межосевое
расстояние;
- межосевое
расстояние; ![]()
![]() - модуль
зацепления;
- модуль
зацепления; ![]()
![]() - передаточное
число редуктора;
- передаточное
число редуктора; ![]()
![]() - угол наклона
зуба
- угол наклона
зуба
Принимаем
![]() ;
;
![]()
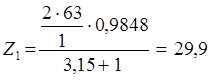
Число зубьев
не может быть дробным, поэтому принимаем ![]()
Число зубьев колеса
![]() ;
; ![]()
Принимаем ![]()
Уточняется угол наклона зуба
![]()
![]()
![]() - входит в
интервал
- входит в
интервал ![]()
Уточняется передаточное число редуктора
![]()
![]()
§ 2.7. Определение основных геометрических параметров шестерни и колеса
Диаметр делительной окружности
![]() , где
, где
![]() - модуль
зацепления;
- модуль
зацепления; ![]()
![]() - число зубьев
зубчатого колеса
- число зубьев
зубчатого колеса
![]() - угол наклона
зуба;
- угол наклона
зуба; ![]()
![]()
![]()
Диаметр окружности выступов
![]()
![]()
![]()
Диаметр окружности впадин
![]()
![]()
![]()
Ширина колеса и шестерни
![]() , где
, где
![]() -
коэффициент ширины колеса;
-
коэффициент ширины колеса; ![]()
![]() - межосевое
расстояние;
- межосевое
расстояние; ![]()
![]()
![]()
![]()
Проверяется межосевое расстояние
![]() ;
; ![]()
§ 2.8. Определение окружной скорости зубчатых колёс и выбор степени точности передачи
![]() , где
, где
![]() - делительный
диаметр шестерни;
- делительный
диаметр шестерни; ![]()
![]() - частота
вращения вала шестерни;
- частота
вращения вала шестерни; ![]()
![]() - назначаем
степень точности передачи – 9 (передача пониженной точности) ([1], табл. 2.6)
- назначаем
степень точности передачи – 9 (передача пониженной точности) ([1], табл. 2.6)
§ 2.9. Определение сил, действующих в зацеплении
Окружная сила
![]() , где
, где
![]() - крутящий
момент на валу колеса;
- крутящий
момент на валу колеса; ![]()
![]() -
делительный диаметр колеса;
-
делительный диаметр колеса; ![]()
![]()
Радиальная сила
![]() , где
, где
![]() - угол
зацепления;
- угол
зацепления; ![]()
![]()
![]() - угол наклона
зуба;
- угол наклона
зуба; ![]()
![]()
Осевая сила
![]()
![]()
![]()
![]()
§ 2.10. Проверка прочности зубьев по контактным напряжениям
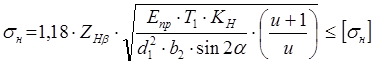 , где
, где
![]() - расчётное
допускаемое напряжение;
- расчётное
допускаемое напряжение; ![]()
![]() -
приведённый модуль упругости материала колёс;
-
приведённый модуль упругости материала колёс;![]() (шестерня и
колесо – стальные)
(шестерня и
колесо – стальные)
![]() -
крутящий момент на валу шестерни;
-
крутящий момент на валу шестерни; ![]()
![]() - делительный
диаметр шестерни;
- делительный
диаметр шестерни; ![]()
![]() - ширина колеса;
- ширина колеса; ![]()
![]() - угол
зацепления;
- угол
зацепления; ![]()
![]()
![]() - передаточное
число редуктора;
- передаточное
число редуктора; ![]()
![]() -
коэффициент повышения прочности косозубых передач по контактным напряжениям
-
коэффициент повышения прочности косозубых передач по контактным напряжениям
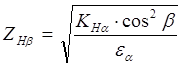 ,
где
,
где
![]() - коэффициент
неравномерности нагрузки;
- коэффициент
неравномерности нагрузки; ![]()
([1], табл. 2.9)
![]() - угол наклона
зуба;
- угол наклона
зуба; ![]()
![]() - коэффициент
торцового перекрытия
- коэффициент
торцового перекрытия
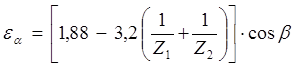
![]()
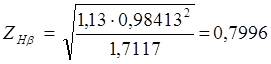
![]() - коэффициент
расчётной нагрузки
- коэффициент
расчётной нагрузки
![]() , где
, где
![]() - коэффициент
концентрации нагрузки;
- коэффициент
концентрации нагрузки; ![]()
![]() - коэффициент
динамической нагрузки;
- коэффициент
динамической нагрузки; ![]()
([1], табл. 2.7)
![]()
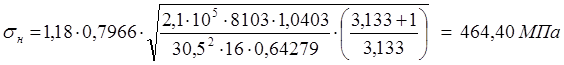
![]()
![]() .
. 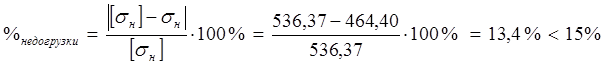
Условие прочности зубьев по контактным напряжениям выполняется
§ 2.11. Проверка прочности зубьев по
напряжениям изгиба Проверка производится для того из пары
зубчатых колёс, для которого отношение ![]() наименьшее (
наименьшее (![]() - допускаемое
напряжение изгиба,
- допускаемое
напряжение изгиба, ![]() -
коэффициент формы зуба).
-
коэффициент формы зуба).
![]()
![]()
Значение ![]() зависит от
приведённого числа зубьев
зависит от
приведённого числа зубьев ![]() и
выбирается по таблице ([1], табл.2.8)
и
выбирается по таблице ([1], табл.2.8)
![]() , где
, где
![]() -
число зубьев зубчатого колеса;
-
число зубьев зубчатого колеса;
![]() -
угол наклона зуба;
-
угол наклона зуба; ![]()
![]()
![]()
![]()
![]()
![]()
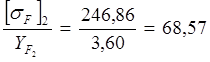
![]() , следовательно,
расчёт проводим для колеса.
, следовательно,
расчёт проводим для колеса.
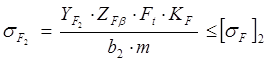 , где
, где
![]() -
допускаемое напряжение изгиба для колеса;
-
допускаемое напряжение изгиба для колеса; ![]()
![]() -
коэффициент формы зуба;
-
коэффициент формы зуба; ![]()
![]() - окружная сила;
- окружная сила;
![]()
![]() -
ширина колеса;
-
ширина колеса; ![]()
![]() - модуль
зацепления;
- модуль
зацепления; ![]()
![]() -
коэффициент повышения прочности косозубых передач по напряжениям изгиба
-
коэффициент повышения прочности косозубых передач по напряжениям изгиба
![]() ,
где
,
где
![]() - коэффициент
неравномерности нагрузки;
- коэффициент
неравномерности нагрузки; ![]()
([1], табл.2.9)
![]() - коэффициент ,
учитывающий повышение прочности на изгиб
- коэффициент ,
учитывающий повышение прочности на изгиб
![]()
![]() - коэффициент
торцового перекрытия;
- коэффициент
торцового перекрытия; ![]()
![]()
![]() -
коэффициент расчётной нагрузки
-
коэффициент расчётной нагрузки
![]() , где
, где
![]() -
коэффициент распределения нагрузки по длине зуба;
-
коэффициент распределения нагрузки по длине зуба; ![]() ([1], табл.2.4)
([1], табл.2.4)
![]() -
коэффициент динамической нагрузки;
-
коэффициент динамической нагрузки; ![]() ([1], табл.2.7)
([1], табл.2.7)
![]()
![]()
![]()
Условие прочности зубьев по напряжениям изгиба выполняется
Глава 3. Расчёт валов
§ 3.1. Проектный расчёт валов редуктора
Предварительно оценивают средний диаметр валов из расчёта только на кручение при пониженных допускаемых напряжениях
![]() , где
, где
![]() - крутящий
момент, передаваемый валом
- крутящий
момент, передаваемый валом
![]() - допускаемое
касательное напряжение для валов редукторов;
- допускаемое
касательное напряжение для валов редукторов; ![]()
Проектный расчёт ведущего вала (вала шестерни)
Средний диаметр вала:
![]()
![]()
![]()
![]()
Ведущий вал соединяется упругой втулочно-пальцевой муфтой с валом электродвигателя, поэтому диаметры этих двух валов необходимо согласовать: диаметр ведущего вала на входе должен удовлетворять условию:
![]()
Из таблицы ([1], табл. П.2) находим диаметр вала электродвигателя 80B4
![]()
Следовательно, ![]()
Найденный средний диаметр вала не удовлетворяет этому условию. Поэтому конструктивно принимаем:
![]() - диаметр вала на
входе
- диаметр вала на
входе
![]() - диаметр вала
под подшипником
- диаметр вала
под подшипником
![]() - диаметр вала
под шестерней
- диаметр вала
под шестерней
![]() - диаметр вала
на выходе
- диаметр вала
на выходе
Проектный расчёт ведомого вала (вала колеса)
Средний диаметр
вала: ![]()
![]()
![]()
![]()
Конструктивно принимаем:
![]() - диаметр вала
на входе
- диаметр вала
на входе
![]() - диаметр вала
под подшипником
- диаметр вала
под подшипником
![]() - диаметр вала
под колесом
- диаметр вала
под колесом
![]() - диаметр вала
на выходе
- диаметр вала
на выходе
§ 3.2. Уточнённый расчёт ведомого вала
Расстояние a
![]() , где
, где ![]() - диаметр
ступицы
- диаметр
ступицы
![]()
![]()
Опорные реакции в вертикальной плоскости
![]()
![]()
![]()
![]() , где
, где ![]() - делительный
диаметр колеса
- делительный
диаметр колеса
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]() ;
; ![]()
Проверка: ![]()
Опорные реакции в горизонтальной плоскости
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Суммарные опорные реакции
Опора А
![]()
![]()
Опора B
![]()
![]()
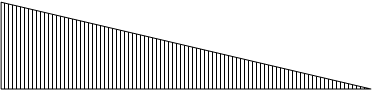
Эпюра вертикальных изгибающих моментов
Сечение I-I
![]()
![]()
![]()
![]()
Сечение II-II
![]()
![]()
![]()
![]()
Максимальный вертикальный изгибающий момент
![]()
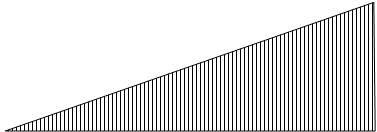
Эпюра горизонтальных изгибающих моментов
Сечение I-I
![]()
![]()
![]()
![]()
Сечение II-II
![]()
![]()
![]()
![]()
Максимальный горизонтальный изгибающий момент
![]()
Суммарный изгибающий момент в опасном сечении
![]()
![]()
Расчётная схема ведомого вала

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()




![]()
![]()
![]() , где
, где
![]() - фактический коэффициент запаса
усталостной прочности при совместном действии напряжений при кручении и изгибе
- фактический коэффициент запаса
усталостной прочности при совместном действии напряжений при кручении и изгибе
![]() -
фактический коэффициент запаса
усталостной прочности при действии напряжений только при изгибе
-
фактический коэффициент запаса
усталостной прочности при действии напряжений только при изгибе
![]() -
фактический коэффициент
запаса усталостной прочности при действии напряжений только при кручении
-
фактический коэффициент
запаса усталостной прочности при действии напряжений только при кручении
Определение Sσ
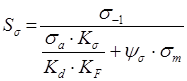 , где
, где
![]() - предел
усталостной прочности материала вала при изгибе
- предел
усталостной прочности материала вала при изгибе
![]() , где
, где ![]() - предел
прочности углеродистой стали;
- предел
прочности углеродистой стали; ![]()
![]()
![]() - амплитуда
цикла напряжений при изгибе
- амплитуда
цикла напряжений при изгибе
![]() - среднее
напряжение цикла при изгибе
- среднее
напряжение цикла при изгибе
Цикл напряжений изгиба является симметричным.
Отсюда следует, что ![]()
![]()
![]()
![]() -
коэффициент, корректирующий влияние среднего напряжения цикла при изгибе на
сопротивление усталости;
-
коэффициент, корректирующий влияние среднего напряжения цикла при изгибе на
сопротивление усталости; ![]()
![]() - эффективный
коэффициент концентрации напряжений при изгибе ([1], табл
- эффективный
коэффициент концентрации напряжений при изгибе ([1], табл
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.