Теорема кодирования Шеннона - теоретическая база помехоустойчивого кодирования. Реализация помехоустойчивого кодирования и его эффективность

МОСКОВСКИЙАВИАЦИОННЫЙ ИНСТИТУТ

(ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Курсовая работа по дисциплине

«основы теории кодирования»

Вариант 4(5)

Серпухов – 2005г.

Оглавление.

Введение.                                                                                                            2

Расчётная часть.      4

Выводы.12

Список использованной литературы.                                                                 13

Введение

Теорема кодирования Шеннона - теоретическая база помехоустойчивого кодирования.

Теорема гласит, что существует некий канал связи и производительность его источника меньше или равна пропускной способности канала связи, то существующий  способ кодирования обеспечивает передачу сообщения с любой малой вероятностью ошибки декодирования этого сообщения. Если производительность источника больше пропускной способности, то такого кода не существует. Очевидно, что пропускная способность канала связи это максимальная скорость передачи информации в канале связи и, при которой обеспечивается заданная достоверность приёма.

Теорема Шеннона утверждает, что помехи в канале связи не исключаются сколь угодно высокой достоверностью декодирования сообщения, а лишь ограничивают максимальной скорость передачи сообщения.

Это вытекает из того, что при введении избыточного кодирования число переданных информационных символов всегда меньше длинны кода n.Поэтому длительность сигналов некоторых сообщений, оказывается меньше чем длинна сигналов кодированного сообщения.

>

Следовательно, помехоустойчивый код принципиально должен быть избыточным.

Анализируя графики зависимости вероятности ошибки как функции  , мы не видим параметров помехоустойчивого кода. Теорема Шеннона не даёт конкретных рекомендаций по построению оптимальных избыточных кодов. На сегодняшний день исследователи проблем передачи информации занимаются вопросами исследования и синтеза корректирующих кодов обеспечивающих максимальную скорость при минимальном фиксированном расстоянии.

Реализация помехоустойчивого кодирования и его эффективность.

Помехоустойчивыми кодами называются коды, обеспечивающие более высокую достоверность приёма по сравнению с простыми (без избыточными) кодами.

Вероятность доведения сообщения является мерой достоверности приёма сообщения.

,где 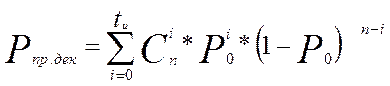- вероятность правильного декодирования.

-количество блоков для передачи 2200 двоичных символов

Для однозначного ответа о положительности и эффективности необходимо найти вероятность ошибки в приёме бита информации (элементарного символа)

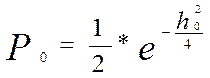 - вероятность ошибки элементарного символа.

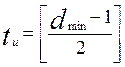- количество исправляемых ошибок.

В ходе исследований установлено, что метод декодирования кодов играет важную роль в определении характеристик статистического декодирования. Оптимальным является декодирование по максимуму правдоподобия.

Задание на курсовую работу.

Исследовать эффективность помехоустойчивого кодирования в системе передачи информации при условиях; длинна сообщения 2200 двоичных символов исследуемые блочные коды (23,12,7) (123,120,3).Вид сигнала А1

Отношение 10≤h₀²≤20

1.Построить статистические характеристики СПИ, характеризующие достоверность приёма информации.

Рассмотрим каждый код в отдельности. Блочный код (23,12,7).Необходимо найти количество исправляемых ошибок. Но при рассмотрении данного кода нам необходимо учитывать, что он потребляет в 2 раза больше энергии, чем код  (123,120,3).

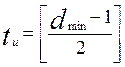                                                                                                                                                                                           (1)

Найдем вероятность ошибки элементарного символа для сигнала А1.

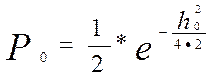при =16                                   (2)

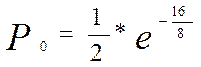
Найдём вероятность правильного декодирования по формуле:

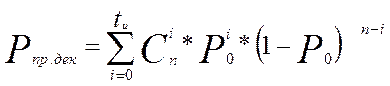                                                       (3)

=

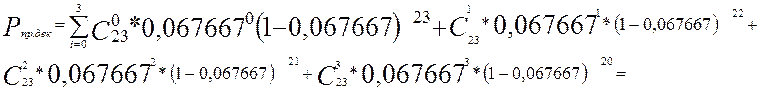
Найдём вероятность ошибки:

                                                                                   (4)

                                                                                       (5)

(количество блоков для передачи 2200 двоичных символов.) Найдём с помощью формулы (5) для  =16 блочного кода (23,12,7).

Рассмотрим блочный код (123,120,3).Необходимо найти количество исправляемых ошибок по формуле 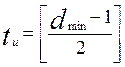(1.1)

                                      (1.1)

Найдем вероятность ошибки элементарного символа сигнала А1. по формуле (2.1)

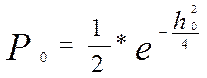при =16                                   (2.1)                                                                    

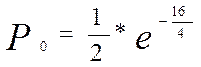
Найдём вероятность правильного декодирования по формуле (3)

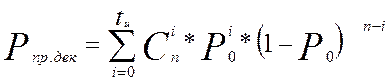                                                       (3.1)

=0,696291

Найдём вероятность ошибки по формуле (4.1)

                                                          (4.1)

Найдём с помощью формулы (5.1) для  =16 блочного кода (123,120,3).

                             (5.1)

(количество блоков для передачи 2200 двоичных символов)

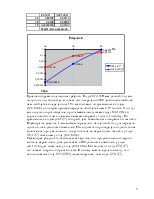
Для построения статистической характеристики необходимо взять ещё несколько точек ,найдём , ,, при другом .

Для кода (23,12,7).

Найдем ошибки элементарного символа для сигнала А1, воспользуемся формулой (2)

при =20

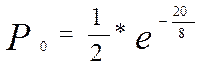=0,041042

Найдём вероятность правильного декодирования по формуле (3)

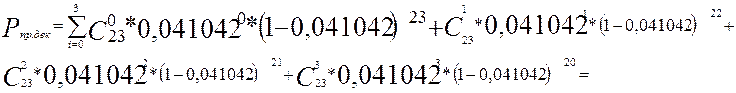
=0,986561

Найдём вероятность ошибки по формуле (4)

Найдём с помощью формулы (5) для  =20 блочного кода (23,12,7).

Для кода (123,120,3) имеем:

Вероятность ошибки элементарного символа для сигнала А1. при =20 по формуле (2.1) равна P0=0,0033