ПЗ – 2. Двухключевые системы защиты информации. Математическая модель и особенности построения НКГС, страница 2

Подчеркнем, что К_С и N должны быть взаимно простыми числами, т.е.

НОД (К_С, N) = 1.

Открытый ключ К_О используется отправителем сообщения для шифрования данных, а секретный ключ К_С используется получателем сообщения для его расшифрования.

Процедура шифрования использует открытый ключ К_О и открытое сообщение М и имеет вид

.

Для вычисления Е используется алгоритм возведения в степень по модулю N.

Обращение функции  , т.е. определение М при известных Е, К_О и N практически неосуществимо при .

Процедура расшифрования криптограммы Е осуществляется на основе секретного ключа К_С получателя и принятой им криптограммы Е на основе следующего выражения

или, что эквивалентно

,

.

Тогда

или  .

В соответствии с теоремой Эйлера

или в общей форме

.

Тогда, заменив х на М запишем

или  .

Именно вследствие указанного вычисление секретного ключа осуществляется  на основе данного выражения.

Таким образом, если криптограмму

возвести в степень К_С, то как результат будет восстановлено исходное сообщение М, так как

.

Поэтому в такой криптосистеме получатель защищает два параметра:

-  секретный ключ К_С;

-  пару чисел P, Q, таких что ;

в тоже время открытыми остаются (помещаются в открытый справочник):

-  значение модуля N;

-  открытый ключ К_О.

Противнику известны N и К_О. Вследствие большой величины N, противник не может за приемлемое время решить задачу факторизации, т.е. разложить N на простые множители, которые выполняют роль «потайного хода» при взятии дискретного логарифма. Если же указанную задачу удалось решить, то в этом случае на основе тройки чисел {P, Q, К_О}, характеризующей «потайной ход» просто осуществляется вычисление функции Эйлера

и противник определяет значение секретного ключа К_С

В связи с этим значение чисел P и Q должны быть очень большими (не менее 100 десятичных знаков).

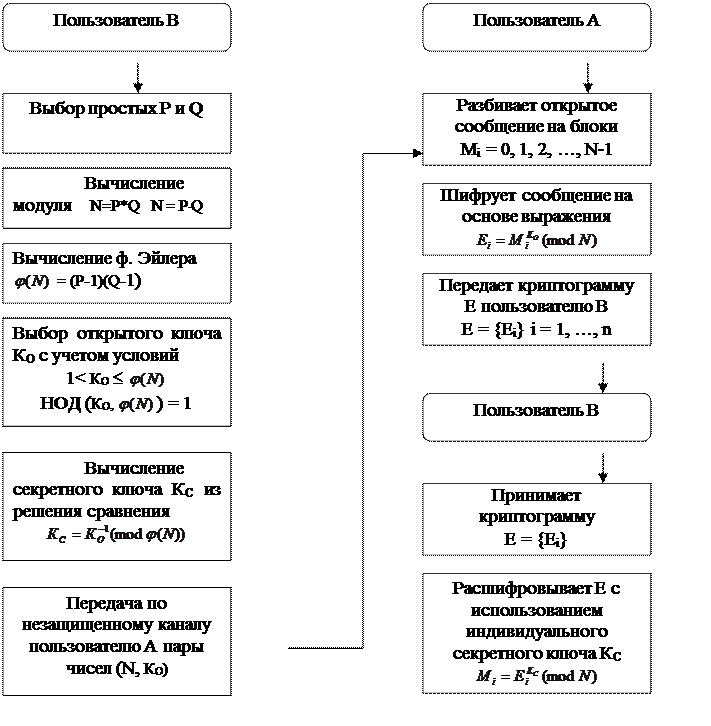
3.  Процедура шифрования и расшифрования по алгоритму RSA

Абонент А – отправитель сообщения, а абонент Б его получатель.

Криптограмма RSA формируется получателем сообщения, в первую очередь для сохранения в тайне значений чисел P и Q.

Последовательность действий пользователей А и Б.

1. Пользователь Б осуществляет выбор двух произвольных больших чисел P и Q.

2. Пользователь Б вычисляет значение

3. Пользователь Б вычисляет функцию Эйлера

и выбирает значение открытого ключа К_О с учетом выполнения условий

,  ,

4. Пользователь Б вычисляет значение секретного ключа К_С, используя расширенный алгоритм Евклида при решении сравнения

5. Пользователь Б пересылает пользователю А пару чисел (N и К_О) по незащищенному каналу

При передачи информации пользователем А пользователю Б, отправитель осуществляет следующие действия:

6. Пользователь А разбивает исходный открытый текст М на блоки, каждый из которых может быть представлен в виде числа М_i

М_i = 0, 1, 2, …, N-1.

7. Пользователь А шифрует текст, представленный в виде последовательности чисел М_i по формуле

и отправляет криптограмму

пользователю Б.

8. Пользователь Б расшифровывает принятую криптограмму

используя секретный ключ К_С

Пример

Занумеруем алфавит

А  Б  В …

1   2  3

Необходимо передать сообщение «ВАБ» ® (3, 1, 2)

1. Действия пользователя Б

1. Выбираем Р = 3, Q = 11

2. Вычисляем модуль N = Р×Q = 3×11 = 33

3. Вычисляет значение функции Эйлера

j(N) = j(33) = (Р-1)(Q-1) = (3-1)(11-1) = 20

и выбирает в качестве открытого ключа К_О число удовлетворяющее условиям

,   НОД (К_О, 20) = 1.

Пусть К_О =7.

4. Вычисляет значение секретного ключа К_С решая сравнение

с применением расширенного алгоритма Евклида.

Перейдем к обозначениям расширенного алгоритма Евклида

Данное уравнение эквивалентно уравнению

Так как , то

или

или

.

Начальный цикл:

1 цикл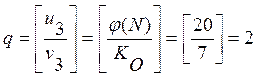   

 следующий цикл

2 цикл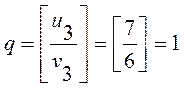  

 следующий цикл

3 цикл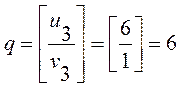  

 

Значит ,  ,

Отсюда  

К_С=3

5. Пользователь Б пересылает пользователю А пару чисел (N=33, К_О=7)

Действия пользователя А

6. Шифрует текст, представленный в виде последовательности чисел М₁, М₂, М₃, используя ключ  К_О=7 и N=33 по формуле

 

Указанное получено с учетом того, что

3¹ º 3 mod 33

3² º 9 mod 33

3⁴ º 81 mod 33

3¹×3² ×3⁴ º 3⁷ = 3×9×15 mod 33= 405 mod 33 = 9 mod 33

2¹ º 2 mod 33

2² º 4 mod 33

2⁴ º 16 mod 33

2¹×2² ×2⁴ º 2⁷ = 2×4×16 mod 33= 128 mod 33 = 29 mod 33

7. Передается криптограмма

Е₁,Е₂,Е₃ = 9,1,29

Действия пользователя Б по расшифровке

8. Осуществляет расшифровку с помощью секретного ключа К_С по формуле

М₁,М₂,М₃ = 3,1,2 ® ВАБ.

Указанное получено с учетом того, что

29¹ º 29 mod 33

29² º 16 mod 33

29¹ ×29² = 29×16 = 464 mod 33 = 2

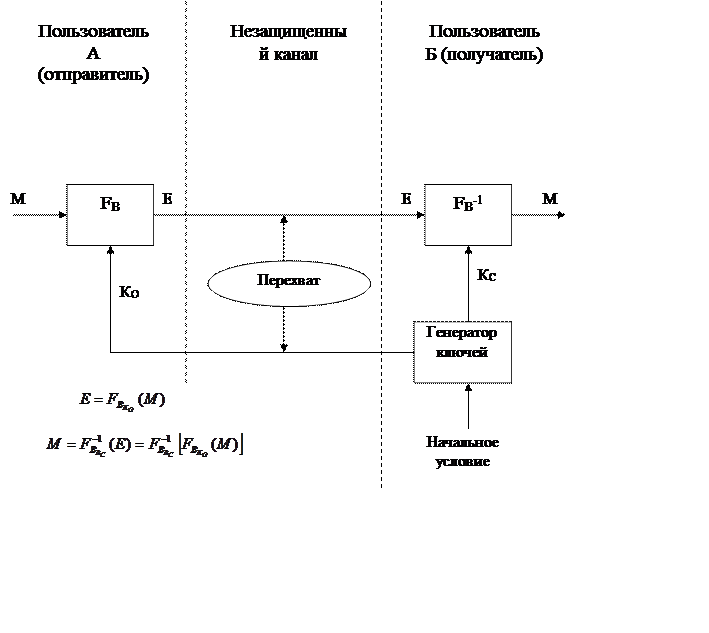
Рис. 1. Обобщенная схема НКГС

Рис. 2. Криптографический алгоритм RSA