Изучение методов криптографической защиты информации. Понятия шифра и кода. Классификация шифров, страница 3

3.  Практические примеры основных систем шифров

3.1. Шифры поточного гаммирования

Данные шифры широко применяются при шифровании цифровых данных. Шифрование производится на основе сложения по модулю т символов (чисел) сообщения и символов (чисел) гаммы шифрующей, формируемой на основе введенного ключа. Восстановление сообщения по принятой криптограмме и известной гамме, которая формируется на приемной стороне с использованием того же ключа, что и на передающей стороне, осуществляется путем вычитания из символов (чисел) криптограммы символов (чисел) гаммы шифрующей. Операция вычитания также осуществляется по модулю т. При использовании такого подхода для зашифрования двоичной информации используется метод линейного двоичного гаммирования, при реализации которого двоичные разряды открытого сообщения складываются по модулю 2 с соответствующими двоичными разрядами гаммы шифрующей.

Ввиду эквивалентности операции сложения по модулю 2 и операции вычитания по модулю 2, как зашифрование, так и расшифрование выполняются с помощью операции сложения по модулю 2:

                                    

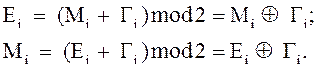
Формирование шифротекста Е_i  и расшифрованного (исходного) текста М_i  в аппаратуре шифрования осуществляется в устройствах (узлах) наложения и снятия шифра соответственно (УНШ, УСШ), ко-торые в простейшем случае представляют собой сумматоры по модулю 2.

Рассмотрим порядок шифрования методом поточного гаммирова-ния, когда в качестве гаммы шифрующей используется апериодичная последовательность символов, например, текст из какой-либо книги. Для этого каждой букве алфавита сопоставим число, соответствующее её порядковому номеру (таблица 1), на основе чего составляются числовые эквиваленты сообщения и гаммы шифрующей. Процесс зашифрования будет определяться выражением , а процесс расшифрования - . Зашифруем сообщение М: ВЫПОЛНИТЬ КОМАНДУ. В качестве ключа используем гамму шифрующую Г:  БЕЗОПАСНОСТЬ СВЯЗИ.

При зашифровании, если в результате сложения числового эквивалента буквы открытого сообщения М с числовым эквивалентом буквы гаммы шифрующей Г получается число больше 31, то из него вычитается модуль 32, например, (14+27) = 41-32 = 9  Й).

Пример зашифрования и расшифрования методом гаммирования приведён в таблицах 2, 3.

При расшифровании из чисел криптограммы Е вычитаются числа гаммы шифрующей М. Если при этом получается отрицательное число, то к нему прибавляется модуль 32 (9 - 27 = -18+32 = 14  О).

Таблица 1

Условные обозначения букв алфавита

Буква	А	Б	В	Г	Д	Е	Ж	З	И	Й	К
Номер	0	1	2	3	4	5	6	7	8	9	10
Буква	Л	М	Н	О	П	Р	С	Т	У	Ф	Х
Номер	11	12	13	14	15	16	17	18	19	20	21
Буква	Ц	Ч	Ш	Щ	Ы	Ь	Э	Ю	Я	-
Номер	22	23	24	25	26	27	28	29	30	31

Примеры зашифрования и расшифрования при линейном двоичном гаммировании приведены в таблицах 4 и 5.

Стойкость шифрования методом поточного гаммирования зависит от структурных свойств гаммы шифрующей и её периода повторения. Наивысшая стойкость шифрования достигается тогда, ко-гда гамма шифрующая является апериодической (неповторяющейся) последовательностью символов.

Таблица 2

Зашифрование методом гаммирования