Протокол статистического исследования показателей здоровья населения. Заболеваемость среди пациентов гастроэнтерологического отделения 3-й городской больницы г.Гомеля, страница 5

V	p	V∙p	V-M	(V-M)2	(V-M)2∙p
10	1	10	-10,8	116,64	116,64
13	1	13	-7,8	60,84	60,84
14	2	28	-6,8	46,24	92,48
15	3	45	-5,8	33,64	100,92
16	1	16	-4,8	23,04	23,04
17	1	17	-3,8	14,44	14,44
18	1	18	-2,8	7,84	7,84
19	2	38	-1,8	3,24	6,48
20	7	140	-0,8	0,64	4,48
21	5	105	0,2	0,04	0,2
22	3	66	1,2	1,44	4,32
24	5	120	3,2	10,24	51,2
27	1	27	6,2	38,44	38,44
29	1	29	8,2	67,24	67,24
55	1	55	34,2	1169,64	1169,64
	∑p=35	∑=727			∑=1758,2

1)  Нахождение моды (М¸).

Мода – это величина варьирующего признака, которая более часто встречается в изучаемой совокупности, т.е. варианта, соответствующая наибольшей частоте. В данном случае мода равна 20.

2)  Нахождение медианы (Ме).

Медиана – это делящая вариационный ранжированный ряд пополам, на две равные половины. Т.к. сумма частот – нечётное число, то Ме= n+1∕2, где n – сумма частот.

Ме= 18 следовательно, место медианы приходится на 18-ю варианту. Эта варианта – 20.

3) Нахождение средней арифметической (М).

В данном случае определяется средняя арифметическая взвешанная, т.к. индивидуальные значения признака повторяются. Вычисляем непосредственным (прямым) способом по формуле:

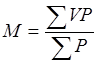 , где p – частота (число случаев) наблюдений каждой варианты.

М=727/35=20,8

4)  Определение среднего квадратичного отклонения (σ).

Определяется непосредственным способом по формуле:

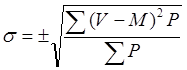
5) Определяем степень разнообразия признаков.

Для этого находим коэффициент вариации:

Если коэффициент вариации более 20% - сильное разнообразие, от 20 до 10% - слабое разнообразие признаков.

В данном случае наблюдается сильное разнообразие признаков, т.к. коэффициент вариации 34,09% (больше 20%).

6) Вычисление средней ошибки средней арифметической:

, где n – число наблюдений.

=1,2

6)  Оцениваем степень достоверности средней арифметической, которая определяется по формуле:

t = M/m

t = 20,8/1,2 = 17,3, т.е. больше 2, следовательно, величина высокодостоверна.

7)Определение доверительных границ:

М_ген = М_выб  t ∙ m_M , где t = 2 при точности исследования 95%

М_ген = 20,8  2 ∙ 1,2 = 20,82,4

Среднее время пребывания пациентов гастроэнтерологического отделения  в стационаре лежит в интервале от 18,4 до 23,2 дней, т.е. от 18 до 23 дней.

3.Графическое изображение данных

1) Линейная диаграмма

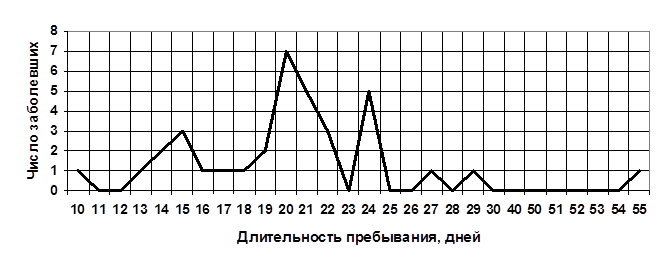
Рисунок 1. Длительность пребывания пациентов в гастроэнтерологическом отделении в январе 1989 г.

2) Столбиковая диаграмма

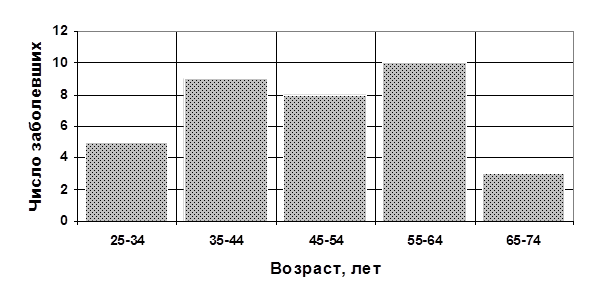
Рисунок 2. Заболеваемость пациентов различных возрастных групп гастроэнтерологическими заболеваниями.

3) Секторная диаграмма

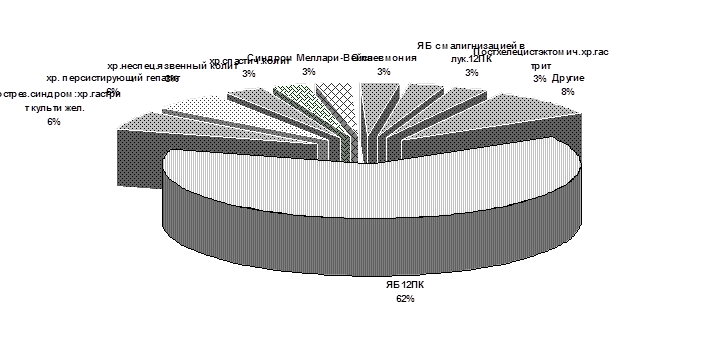
Рисунок 3. Характер заболеваний у пациентов, поступивших в гастроэнтерологическое отделение в январе 1989 г.

IV этап.Заключение (анализ и выводы).