Данные о численности населения, числе родившихся и умерших в регионе. Коэффициенты рождаемости, смертности, естественного прироста населения, жизненности по годам

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

Учреждение высшего профессионального образования

«Комсомольский - на - Амуре государственный

Технический университет»

Факультет экономики и менеджмента

Кафедра «Экономика и финансы»

РАСЧЁТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ

По дисциплине «Статистика»

Экономическая статистика

Студент группы 0МО-1                                                                         

Преподаватель                                                                                         

2012

Задача 1:

Вариант№2

Представлены данные о численности населения, числе родившихся и умерших в регионе.

Год	Население на начало годы, тыс. чел.	Число родившихся, чел.	Число умерших, чел.
2000	2000	55000	40000
2001	2100	59000	45000
2002	2500	75000	45000
2003	2250	30000	25000
2004	2300	40000	35000
2005	2400	42000	40000
2006	2550	-	-

Определите: 1) среднюю численность населения за каждый год. 2) коэффициенты рождаемости, смертности, естественного прироста населения, жизненности по годам; 3) погодовые балансы динамики численности населения.

Решение:

1.  Определим среднюю численность населения за каждый год:

чел.

 чел.

чел.

чел.

чел.

чел.

2. Общий коэффициент рождаемости показывает число родившихся в расчете на 1000 чел. населения:

.

 ‰

 ‰

 ‰

 ‰

 ‰

 ‰

Общий коэффициент смертности характеризует число умерших в расчете на 1000 чел населения:

.

 ‰

 ‰

 ‰

 ‰

 ‰

 ‰

Коэффициент естественного прироста населения показывает, насколько увеличилась или уменьшилась численность населения за счет естественных факторов (рождаемости и смертности) в расчете на 1000 чел:

‰ или .

 ‰

 ‰

 ‰

 ‰

 ‰

 ‰

Коэффициент жизненности характеризует соотношение между уровнем рождаемости и смертности:

 или  .

 

 

 

 

 

 

3. Составим погодовые балансы динамики численности населения

Год	S тыс. чел.		Абсолютный прирост	в тыс. чел. За счёт
2000	2000	2100	100	15	85
2001	2100	2500	400	14	386
2002	2500	2250	-250	30	-280
2003	2250	2300	50	5	45
2004	2300	2400	100	5	95
2005	2400	2550	150	2	148
Итого	200	2550	550	71	479

Задача 6:

Вариант №2

Охарактеризуйте динамику безработицы, рассчитав за каждый год для всех безработных, молодежи, женщин:

1.  среднюю продолжительность безработицы;

2.  структуру продолжительности безработицы.

Изобразите динамику рассчитанных показателей графически. Сделайте выводы.

Продолжительность безработицы	Всего чел.	Из них
		молодежь 16 – 29 лет	женщины
До 1 месяца	3750	930	1850
От 1 до 4 месяцев	9400	2380	5300
От 4 до 8 месяцев	6220	2050	4670
От 8 до 1 года	5640	1250	3480
Более 1 года	3230	530	1830
Всего:	28240	7140	17430

Решение:

1. Определим среднюю продолжительность безработицы с помощью средней арифметической взвешенной:

Ч_безр. =  чел.

Ч_{безр. мол.} =  чел.

Ч_{безр. жен.} =  чел.

2. Определим структуру продолжительности безработицы:

Продолжительность безработицы	Всего чел.	Из них
		молодежь 16 – 29 лет	женщины
До 1 месяца	3750/28240=0,133	930/7140=0,130	1850/17430=0,106
От 1 до 4 месяцев	9400/28240=0,333	2380/7140=0,333	5300/17430=0,304
От 4 до 8 месяцев	6220/28240=0,220	2050/7140=0,287	4670/17430=0,268
От 8 до 1 года	5640/28240=0,2	1250/7140=0,175	3480/17430=0,199
Более 1 года	3230/28240=0,114	530/7140=0,075	1830/17430=0,105
Всего:	1	1	1

Изобразим динамику рассчитанных показателей графически.

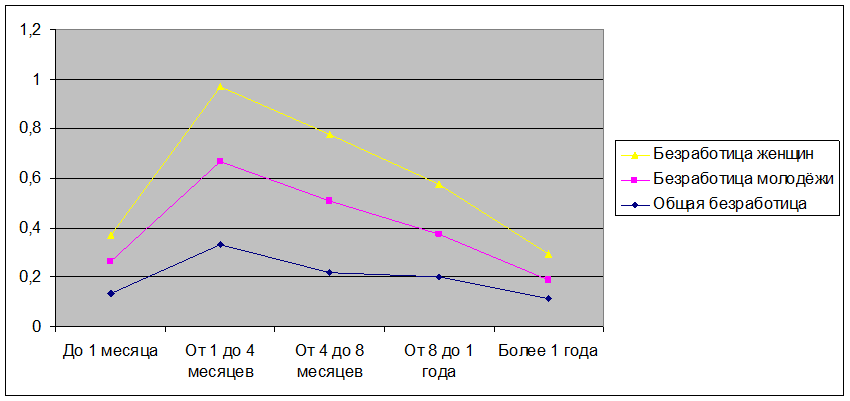
Вывод: Наибольшая численность безработицы зарегистрирована продолжительностью от 1 до 4 месяцев. Наименьшая численность безработицы зарегистрирована продолжительностью более 1 года.

Задача 10:

Вариант №2

Планом предусмотрены следующие показатели:

Показатель	Вариант 1
Средняя месячная выработка на одного рабочего	2068
Средняя дневная выработка	94
Средняя часовая выработка	12
Фактически за отчетный месяц
Выпуск продукции (тыс. р.)	255,6
Среднесписочное число рабочих, чел	120
Число отработанных рабочими чел.-дней	2520
Число отработанных рабочими чел.-часов	19404

Определите индексы средней часовой, дневной и месячной производительности труда.

Решение:

Определим индекс средней месячной производительности труда:

 - средняя месячная производительность труда на 5 % меньше месячной производительности, предусмотренной планом.

Определим индекс средней дневной производительности труда:

 - средняя дневная производительность труда на 0,125 % меньше дневной производительности, предусмотренной планом.

Определим индекс средней часовой производительности труда:

 - средняя часовая производительность труда на 0,125 % меньше часовой производительности, предусмотренной планом.

Задача 21:

По предприятию, начавшему деятельность 27 марта, имеются следующие данные о списочной численности рабочих: 27 марта – 500, 28 марта – 500, 29 и 30 марта – выходные дни, 31 марта – 533 чел. Заполните соответствующими показателями пустые клетки таблицы.

Определите прироста фонда заработной платы во втором квартале по сравнению с первым, вызванный ростом численности рабочих и изменение среднего заработка.

Решение:

Показатели	Март	1-й кв.	Апрель	Май	Июнь	2-й кв.	Первое полугодие
Среднее списочное число рабочих	506,6	168,9	520	515	523	519,3	344,1
Фонд заработной платы рабочих, тыс. р.	1291,83	1291,83	1840	1880	5620 – 1840 – 1880 = 1900	5620	1291,83 + 5620 = 6911,83
Средняя заработная плата одного списочного рабочего, р.	2550	850	1840000 / 520 = 3538,5	3650,5	3632,9	3607,3	1728,65

Средняя списочная численность работников () за месяц определяется путем деления суммы численности работников списочного состава () за все календарные дни месяца на число календарных дней (Дк) в данном месяце (28, 29, 30, 31). При этом списочная численность работников за выходные и праздничные дни приравнивается к списочной численности персонала предыдущего рабочего дня. Методика расчета не меняется и в том случае, когда вновь организованное предприятие начало работать не с начала месяца.

Среднесписочная численность за март:

 чел.

За период, состоящий из нескольких месяцев, средняя списочная численность определяется как средняя величина из показателей средней списочной численности за все месяцы данного периода. Если предприятие начало работать не с начала периода (квартала, года), то средняя списочная определяется путем деления суммы среднесписочной численности за каждый месяц периода работы  на полное число месяцев в данном периоде.

Определим прироста фонда заработной платы во втором квартале по сравнению с первым:

∆ФЗП = 5620 – 1291,83 = 4328,17 тыс. р.

Задача 32:

Имеются следующие данные об основных фондах строительного предприятия:

Сумма износа на начало года, тыс. р.	300
Процент износа на начало года	20
1 мая введено в эксплуатацию новых основных фондов, тыс. р.	5
1 августа куплено у других строительных организаций, тыс. р.	20
Процент износа поступивших фондов	10
1 июля выбыло основных фондов по полной стоимости, тыс. р.	18
процент износа выбывших фондов	80
Среднегодовая норма амортизации, %	10

Определите: 1) стоимость основных фондов на конец года: а) полную первоначальную; б) первоначальную с учетом износа; 2) среднегодовую стоимость основных фондов; 3) коэффициенты обновления и выбытия основных фондов; 4) коэффициент износа и годности основных фондов на конец года.

Решение:

Определим полную первоначальную стоимость основных фондов на начало года:

Ф_н.г. = 300/0,20 = 1500 тыс. р.

Тогда на начало года первоначальная стоимость с учетом износа составит:

Ф'_н.г. = 1500 – 300 = 1200 тыс. р.

Определим среднегодовую стоимость фондов предприятия

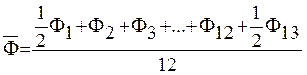
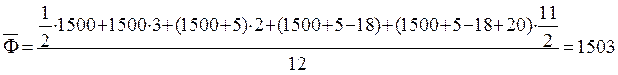 тыс. р.

Определим полную стоимость основных фондов на конец года: