Если нелинейность однозначна, тогда g'(A)=0.
Характеристика НЭ всегда такова, что в уравнении 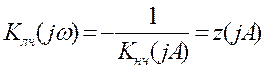 график
зависимости
график
зависимости 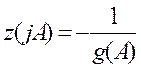 представляет собой
отрицательный участок на оси абсцисс.
представляет собой
отрицательный участок на оси абсцисс.
Такой нелинейностью может быть, например, транзисторный усилитель мощности (нелинейность с ограничением).
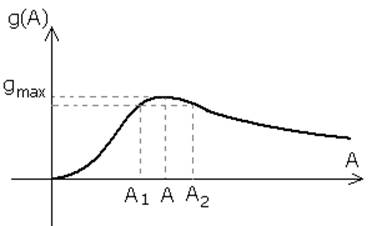
Если
порядок линейной части системы не ниже третьего, а 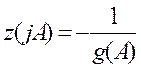 принимает
вид характеристики
принимает
вид характеристики ![]() , тогда в системе могут возникнуть
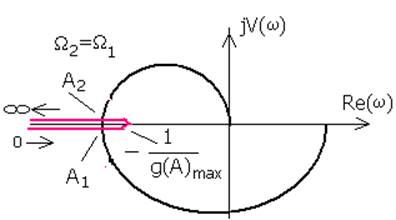
автоколебания. Частота этих колебаний, как следует из рисунка, соответствует
значению
, тогда в системе могут возникнуть
автоколебания. Частота этих колебаний, как следует из рисунка, соответствует
значению ![]() , при которой
, при которой ![]() (частотная характеристика
линейной части системы) пересекает ось абсцисс в ее отрицательных значениях, и
не зависит от вида нелинейного элемента!
(частотная характеристика
линейной части системы) пересекает ось абсцисс в ее отрицательных значениях, и
не зависит от вида нелинейного элемента!
Оценка симметричных автоколебаний
при наличии динамической нелинейности
Сложней анализировать симметричные автоколебания в динамической системе.
Как и ранее, колебания в системе определяются
знаменателем операторного выражения 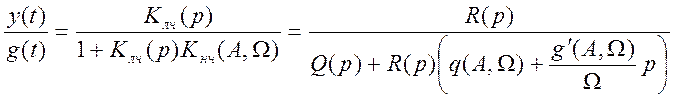 , то есть
уравнением
, то есть
уравнением 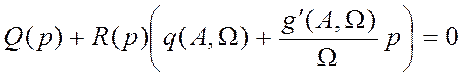 .
.
После подстановки ![]() последовательно
получают:
последовательно
получают:
![]() ,
,
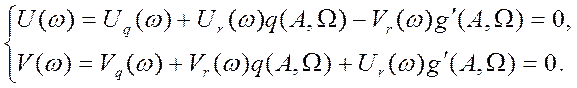
Полученная система уравнений решается относительно ![]() и
и ![]() ,
которых может быть достаточно много. Каждое из найденных решений необходимо проверить
на устойчивость режима автоколебаний по удовлетворению неравенству:
,
которых может быть достаточно много. Каждое из найденных решений необходимо проверить
на устойчивость режима автоколебаний по удовлетворению неравенству:
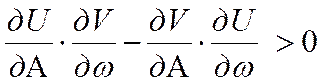 .
.
РЕЗЮМЕ:
Симметричные автоколебания имеют ограниченную область применения. Их обычно создают в реальных системах позиционирования для борьбы с сухим трением в механических узлах электромеханических систем. (Следящие системы, состоящие в состоянии покоя. Вот около покоя и создается сухое трение, которое делает систему неминемальнофазной).
Несимметричные автоколебания в НСАУ
Несимметричные автоколебания в системах автоматического управления характеризуются тем, что гармонический сигнал на входе нелинейного элемента смещен относительно нуля, а на выходе его есть постоянная составляющая.
|
|
Здесь D – электродвигатель, ДОС – датчик обратной связи. Нелинейным элементом является усилитель мощности. |
Пусть
на входе нелинейного элемента (реле с зоной нечувствительности) имеется сигнал
![]() , где
, где ![]() -
это постоянный сигнал, а
-
это постоянный сигнал, а ![]() (на постоянный
сигнал наложена гармоника).
(на постоянный
сигнал наложена гармоника).
В
этом случае выходной сигнал НЭ (см. ![]() ) зависит от постоянной составляющей и
частоты входного сигнала.
) зависит от постоянной составляющей и
частоты входного сигнала.
|
|
Разложение
в ряд Фурье будет иметь вид:
Как и ранее, при гармонической линеаризации воспользуемся только первой гармоникой. Аналогичная ситуация может возникнуть и в случае несимметричной нелинейности. |
Коэффициенты гармонической линеаризации
при несимметричных автоколебаниях
Итак,
на входе НЭ действует сигнал: ![]() . Иногда, если
НЭ несимметричный, постоянная составляющая х0 может быть равна
нулю. В общем случае коэффициенты гармонической линеаризации определяются по
формулам:
. Иногда, если
НЭ несимметричный, постоянная составляющая х0 может быть равна
нулю. В общем случае коэффициенты гармонической линеаризации определяются по
формулам: 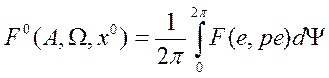 ,
,
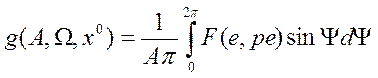 ,
,
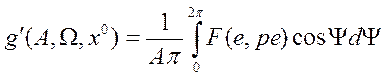 .
.
Характеристика НЭ может быть представлена следующим выражением:
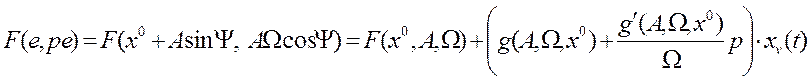 .
.
Структура НСАУ при несимметричных автоколебаниях
Рассмотрим НСАУ первого класса с динамическим воздействием на входе:

Здесь
![]() - задание и
- задание и ![]() ,
, ![]() ,
,
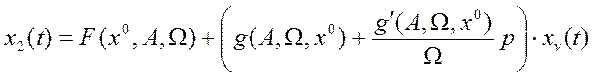 ,
, ![]() ,
,
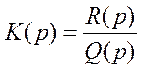 . Объединив все эти выражения,
получим:
. Объединив все эти выражения,
получим:
![]()
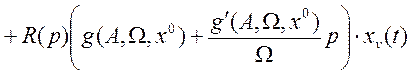 .
.
Так
как на входе НЭ действует сигнал ![]() процессы в
системе (в силу ее линейного представления) разбиваются на два уровня:
процессы в
системе (в силу ее линейного представления) разбиваются на два уровня:
- установившееся движение,
- гармонические колебания.
Выделим уравнение для установившегося процесса:
![]() , где
, где ![]() - эквивалентный входной сигнал
(положим его постоянным), и уравнение гармонических колебаний:
- эквивалентный входной сигнал
(положим его постоянным), и уравнение гармонических колебаний:
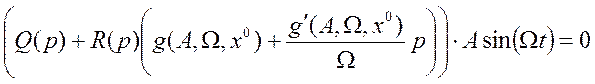 .
.
Из уравнения установившегося процесса определяется величина
смещения ![]() и подставляется в уравнение
колебательного движения (в коэффициенты гармонической линеаризации). В
результате получают операторное уравнение
и подставляется в уравнение
колебательного движения (в коэффициенты гармонической линеаризации). В
результате получают операторное уравнение 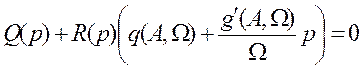 ,
разрешаемое относительно
,
разрешаемое относительно ![]() и
и ![]() .
.
В случае с однозначной нечетно-симметрической нелинейностью характеристическое уравнение упрощается и принимает вид:
![]() , а после
подстановки
, а после
подстановки ![]() последовательно получают:
последовательно получают:
![]() ,
,
![]() , откуда
, откуда
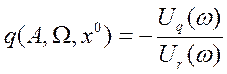 и
и ![]() .
.
Полученные соотношения позволяют заключить, что при
однозначной нелинейности частота ![]() несимметричных
колебаний остается такой же, как и при симметричных, независимо от величины
смещения
несимметричных
колебаний остается такой же, как и при симметричных, независимо от величины
смещения ![]() и параметров нелинейности. Амплитуда
же несимметричных колебаний зависит от смещения и выражается через амплитуду
симметричных, так как
и параметров нелинейности. Амплитуда
же несимметричных колебаний зависит от смещения и выражается через амплитуду
симметричных, так как ![]() . То есть обе
величины
. То есть обе
величины ![]() однозначно определяются параметрами
линейной части.
однозначно определяются параметрами
линейной части.
Рассмотрим НСАУ с нелинейностью релейного типа:

Здесь
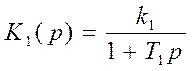 ,
, 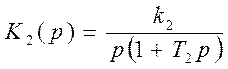 .
.
Гармоническая линеаризация нелинейности при симметричных колебаниях дает:
![]() , где
, где 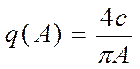 , а
при несимметричных:
, а
при несимметричных: ![]() , где
, где
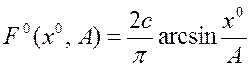 ,
, 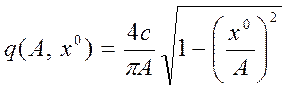 .
.
Уравнение замкнутой системы относительно переменной х имеет вид:
![]() .
.
При
симметричных колебаниях, когда g(t)=0 (или pg(t)=0), имеем характеристическое
уравнение 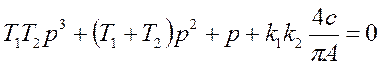 . Подставив
. Подставив ![]() , получим:
, получим:
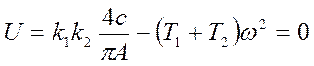 и
и ![]() , откуда
, откуда 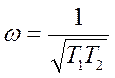 ,
, 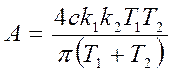 .
.
В
случае несимметричных колебаний при входном воздействии ![]() , в соответствии с полученным
выше, имеем уравнение для постоянных составляющих:
, в соответствии с полученным
выше, имеем уравнение для постоянных составляющих: 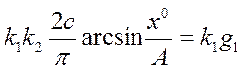 ,
откуда
,
откуда 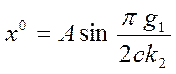 . Подстановка
. Подстановка ![]() в
в ![]() дает:
дает:
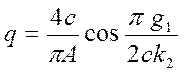 .
.
Теперь
для определения амплитуды А несимметричных автоколебаний используем равенство ![]() (равенство коэффициентов
гармонической линеаризации при наличии и отсутствии симметрии в выходном
сигнале):
(равенство коэффициентов
гармонической линеаризации при наличии и отсутствии симметрии в выходном
сигнале): 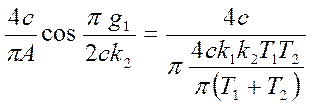 , откуда получаем
, откуда получаем 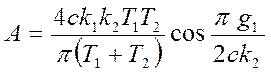 . Тогда постоянная составляющая
(смещение) будет найдена в виде:
. Тогда постоянная составляющая
(смещение) будет найдена в виде:
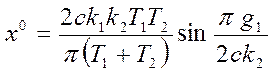 . Частота колебаний, как уже было
отмечено, не изменится.
. Частота колебаний, как уже было
отмечено, не изменится.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.