Методы оценки шумов квантования по уровню дискретных преобразователей информации в ЭМС. Основная расчетная модель ДСАУ, её передаточные функции и спектральные плотности случайных воздействий, страница 2

                              U_ц (t)

              N

Рис. 5. 3. Модель ЦАП в блоке "2".

Блок ЦАП "2" (см. рис.2. 3) с линеаризованной характеристикой и коэффициентом передачи  и помехой U_Ц(t) изображен на рис.5. 3.

После этих преобразований расчетная модель ДСАУ приобретает вид рис 6. 3.

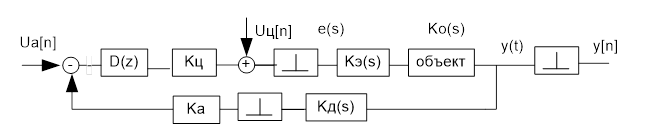
Рис. 6. 3.Расчетная модель  помех в ДСАУ.

Здесь , сигнал управления g(t) = 0, считаем сигналом на входе помеху U_A[n,].

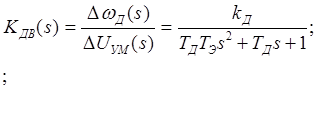
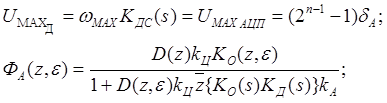
Следует выбрать АЦП и ЦАП с равными аналоговыми квантами, тогда соблюдается такое равенство

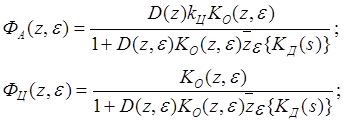                                                    (1. 3.)

Яков Залманович Цыпкин, предложил считать U_A[n], и U_Ц[n] - случайными величинами, типа белого шума, тогда:е

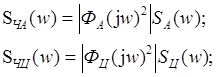                                                                          (2. 3.)

Спектральная плотность входных сигналов, в плоскости "w"будет.

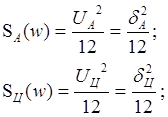                                                                                   (3. 3)

Для дисперсии непрерывной функции имеём такое выражение :

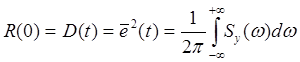                                                                (4. 3.)

Здесь полагаем, что спектральная плотность сигнала выхода S_у(ω) будет такой:

.                                                                                     (5.3.)

4.3.Погрешности от шумов квантования в преобразователях информации ДСАУ

По аналогии с выражениями (4.3.) и (5.3.) могут быть вычислены.

Дисперсия составляющей ошибки АЦП:

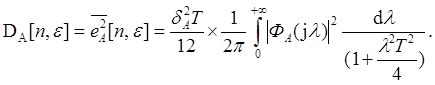                                              (6.3.)

Дисперсия составляющей ошибки ЦАП:

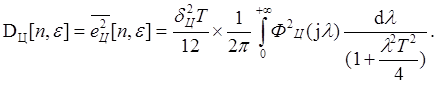                                                (7.3)

Примечание 2. Покажем преобразование формулы (4. 3.),с помощью выражений [(1. 3) - (4. 3.)], на примере (6. 3).Поскольку белый шум имеет постоянную амплитуду [см. выражение (2. 3)], то эта постоянная величина может быть выведена из под интеграла. Кроме того, функция - четно - симметричная. Поэтому интеграл (4. 3)может быть записан так 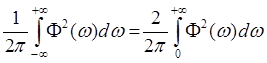 .Теперь заменим dω.  Используем выражение:

, тогда

 Отсюда .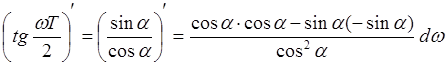

Следователь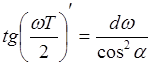но , но.

 Поэтому 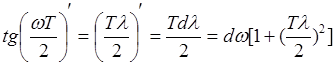 .Отсюда имеем:   (*)

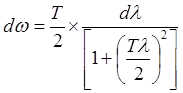Последнее выражение (*) определяет значения коэффициентов и окончательный вид

формул (6. 3.) и (7.3.)

Сложности исследования не ограничиваются только этим. Вычисление определенных интегралов (6. 3.) и (7. 3.) выполняются по известной в Теории управления теореме (закону)"Парсеваля - Релея",( которую изучали в первой части курсаТУ) [52, часть1]. Известно, что погрешность от "шума "квантования  может быть бóльшей на "смещенных" характеристиках, поэтому принимают  и вычисляют

 ,                                                          (8. 3.)

гдесреднеквадратичное значение амплитуды стационарных колебаний угловой скорости привода, вызванное шумами квантования преобразователей информации.

Величину  σ _ш необходимо "увязать" со значением предельного значения коэффициента неравномерности вращения к _{н ,} указанного в табл. 2 при заданном ( или требуемом  в техническом задании ) диапазоне регулирования скорости привода.

,                                                                                        (9. 3)

где γ допустимая доля σ _ш в максимальном отклонении Δω_max  угловой скорости привода в режиме стационарных колебаний.

В свою очередь Δω_max   можно определить  следующим образом:

,    (10.3)

где ω₀ среднее значение угловой скорости привода в данном диапазоне и к _н относительная величина в данном диапазоне (см. табл.2)

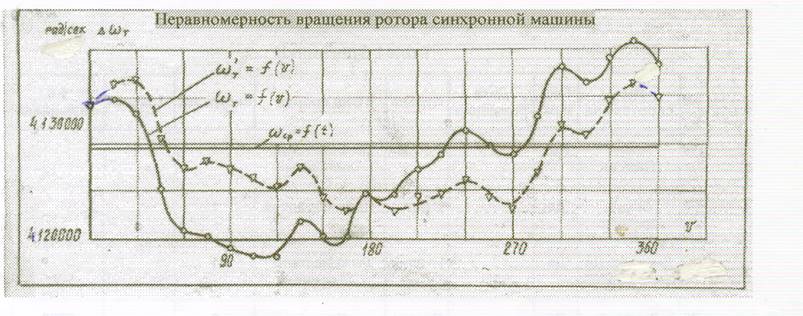
Примечание 3.Рассмотрим конкретный, но очень важный пример. Как было показано в диссертации П. Факадея (см стр. 4 текста данной лекции) шумы квантования преобразователей информации несущественно изменят суммарную статическую ошибку системы привода. Но иначе обстоит дело со стационарными колебаниями скорости . На рис.7. 3. мы приводим экспериментально полученную зависимость мгновенной скорости вращения вала синхронной машины.  Её номинальная скорость 157рад\с, средняя скорость

ω₀=4,1267228рад\с. Диапазон регулирования скорости:

 

Колебания, вызванные изменением сил трения в опорах подшипников качения, Δ=0,00616рад\с. Колебания, вызванные изменением сил трения в опорах подшипников качения и асимметрией питания статора , Δ=0,00913рад\с.

Рис.7.3 Кривая мгновенных колебаний угловой скорости синхронной машины вдоль расточки статора (по его угловым положениям)

При диапазоне регулирования скорости до d=1:100  получим рад\с .

По формуле (10. 3) можно определить допустимую величину γ=0,8 для расчета , т.к. доля прочих возмущений невелика (не более 15%).

0,1468

Но, если диапазон регулироваприя скорости расширить до d=1:1000, то  только относительное значение δ_АТ составит 146%. Поэтому нужно будет думать о снижении потерь в станке повышении  точности подшипников двигателя, точности преобразователя частоты , замене в приводе синхронного двигателя и прочих  возникших проблемах, а не "шумах"

АЦП и ЦАП.

Лекцию записал  Дробинский Д.16.10 2009, скорректировал  Живописцев Д.С. 29.10.10