В базовом варианте модели Солоу в стационарном состоянии объем капитала (К) и потребление (С) растут с тем же темпом, что и население являются неизменными падают, если норма сбережения больше нормы амортизации растут, если норма сбережения больше нормы амортизации
В базовом варианте модели Солоу в стационарном состоянии капиталовооруженность и потребление на душу населения растут с тем же темпом, что и население являются неизменными падают, если норма сбережения больше нормы амортизации растут, если норма сбережения больше нормы амортизации
В модели Солоу с тудосберегающим техническим прогрессом в стационарном состоянии объем капитала (К) и уровень выпуска (Y)
растут с постоянным темпом, равным темпу технического прогресса растут с темпом, равным темпу роста населения плюс темп технического прогресса растут, если норма сбережения больше нормы амортизации являются неизменными
В модели Солоу с тудосберегающим техническим прогрессом в стационарном состоянии капиталовооруженность и потребление на душу населения растут с постоянным темпом, равным темпу технического прогресса растут с темпом, равным темпу роста населения плюс темп технического прогресса растут, если норма сбережения больше нормы амортизации являются неизменными
В модели Солоу с тудосберегающим техническим прогрессом в стационарном состоянии капитал и потребление на одного эффективного рабочего растут с постоянным темпом, равным темпу технического прогресса растут с темпом, равным темпу роста населения плюс темп технического прогресса растут, если норма сбережения больше нормы амортизации являются неизменными
![]()
Золотым правилом накопления капитала является выражение
Уравнением накопления капитала является выражение в базовом варианте модели Солоу
Стационарная величина капиталовооруженности определяется из условия
Уравнением накопления капитала при наличии трудосберегающего технического прогресса является выражение
![]()
![]()
![]()
![]()
Нейтральный (по Хиксу) технический прогресс может быть описан следующей производственной функцией
Трудосберегающий технический прогресс может быть описан следующей производственной функцией
Капиталосберегающий технический прогресс может быть описан следующей производственной функцией
![]()
При наличии технического прогресса стационарное состояние в модели Солоу совместимо только с трудосберегающим техническим прогрессом капитолосберегающим техническим прогрессом нейтральным по Хиксу техническим прогрессом нейтральным по Солоу техническим прогрессом
Эластичность функций
Изучение эластичности соответствующей функции позволяет определить динамику спроса населения на данное благо или товар при изменении его цены динамику спроса на данное благо или товар при изменении доходов населения эффективность тех тили иных затрат изменение прибыли предприятия под воздействием различных факторов
Функция y=f(x) задана табличным способом. Два соседних значения аргумента равны х1=4 и х2=2, а значения функции соответственно у1=10 и у2=20. Тогда средняя эластичность равна
-2
-1
1
2
Функция y=f(x) задана табличным способом. Два соседних значения аргумента равны х1=4 и х2=2, а значения функции соответственно у1=10 и у2=20. Тогда дуговая эластичность равна
-2
-1
1
2
Функция y=f(x) задана табличным способом. Два соседних значения аргумента равны х1=4 и х2=2, а значения функции соответственно у1=10 и у2=20. Тогда процентная эластичность равна
-2
-1
1
2
Функция y=f(x) задана табличным способом. Два соседних значения аргумента равны х1=4 и х2=2, а значения функции соответственно у1=10 и у2=20. Тогда конечная эластичность равна
-2
-1
1
2
Процентная эластичность дискретной функции вычисляется по формуле
Конечная эластичность дискретной функции вычисляется по формуле
Средняя эластичность дискретной функции вычисляется по формуле
Дуговая эластичность дискретной функции вычисляется по формуле
Логарифмическая эластичность дискретной функции вычисляется по формуле
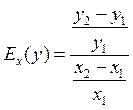 |
 |
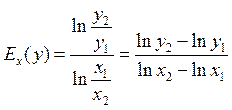 |
|||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.