Анализ межотраслевых связей. Схема и модель межотраслевого баланса (МОБ) производства и распределения продукции. Исследование и решение системы уравнений МОБ

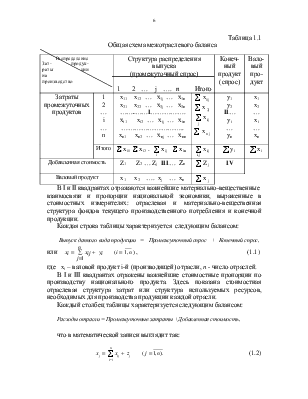
Прямые поставки продукции из цеха потребителю запрещены, потребитель получает готовую продукцию со складов. Определить оптимальный план перевозок, минимизирующий суммарные затраты. Склады на первом этапе являются потребителями продукции, на втором – поставщиками, поэтому им в таблице отводятся столбцы как потребителям и строки как поставщикам. Так как  потребители получают продукцию со складов, запретим прямые поставки тарифами , что обеспечивает условие оптимальности для клеток с , так как для этих клеток характеристики  на всех этапах решения.

Перевозки со склада на склад также запрещены, они блокируются запретительными тарифами М. Разрешается поставка склада самому себе, что означает размер неиспользованной мощности склада.

Заполним по методу минимального элемента сначала блок таблицы, в котором отражаются перевозки продукции со складов потребителям, затем фиктивную диагональ, затем перевозки от поставщиков на склады. Получим следующую таблицу.

План х₁

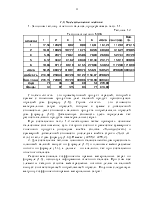
Для этого плана общие издержки состовят: Z₁=6290. Число занятых клеток в таблице m+n-1=5+5-1=9. Далее решаем задачу методом потенциалов.

Рассчитав потенциалы и характеристики для этого плана по аналогии с предыдущим, видим, что полученный план х₁ неоптимальный, так как . Строим для клетки (5,4) контур (5,4)-(5,3)-(4,3)-(4,4)-(5,4) и перемешаем по нему поставку = 200. Получим план х₂. При этом  z уменьшится на величину , в соответствии с экономическим смыслом характеристики

План х₂ оптимальный, так как все характеристики свободных клеток неотрицательны, и не единственный,  

Поставка в фиктивную диагональ х₅₂=200  означает размер неиспользованной мощности второго склада.

План х₂

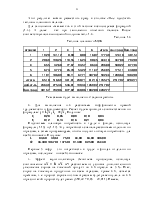
6.3.  Варианты для выполнения задания №6

Условия заданий те же, что и в рассмотренном примере.

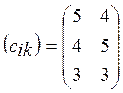
Прямые поставки продукции из цехов потребителям запрещены.

Задание №7

7. Управление запасами

При  решении задачи управления запасами в основном необходимо ответить на два вопроса: когда запасы подлежат пополнению и  каков объем пополнения запасов. А это, в свою очередь, необходимо для решения следующих двух задач: удовлетворить спрос на определенную продукцию и минимизировать суммарные издержки по обеспечению спроса на определенном уровне.

Разработано большое количество моделей оптимального управления запасами. Из всего этого множества  рассмотрим лишь следующие три модели:

·  модель определения оптимального уровня запаса;

·  модель определения оптимальной партии изделий;

·  модель запасов с дефицитом;

В зависимости от того или иного типа модели каждый раз оптимальный уровень запаса определяется из условия минимизации суммарных издержек, в которые включаются разные составляющие. При этом  действуют разные предпосылки относительно времени реализации поставки.

Рассмотрим последовательно реализацию каждой модели из приведенного списка.

Первая модель является базовой и определяется в предположении, что известны спрос на продукцию, издержки хранения единицы запаса и издержки оформления одного заказа, а также предполагается, что интенсивность  расходования запаса постоянна, а  поставка осуществляется мгновенно. Оптимальный уровень заказа в этом случае определяется из условия минимизации издержек хранения и заказывания. Обозначим их соответственно через  THC и TOC. Тогда общие издержки составят: TIC = THC + TOC.

Введем обозначения:

Q – величина одного заказа;

c_о – издержки оформления одного заказа;

D – величина спроса на продукцию;

c_h – издержки хранения ед. товара.

Тогда, THC = c_h Q/2, a TOC = c_o D/Q, следовательно,

TIC = c_h Q/2 + c_o D/Q. Минимизируя эту величину, получим известную формулу Уилсона:

Q^* = .

Приведем решение задачи по этой модели.

Пусть D = 5 000, C_o = 15, C_h = 10.

Тогда Q^* = =122.47.

Определим другие характеристики системы.

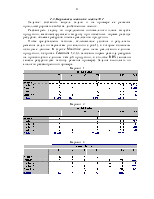
THC = c_h Q^*/2 = 10^.122.47/2 =  612.37, TOC = c_o D/Q^* = 15^.5000/122.47 = 612.37. Совпадение этих величин не случайно. В точке минимума суммарных издержек кривые издержек заказывания и хранения пересекаются, как это видно из рис.9.

Рис. 9.Графическое решение задачи

Прямая линия здесь характеризует издержки хранения (Holding Cost), равные (Q/2)c_h, гипербола - издержки заказывания (Setup Cost), равные (D/Q)c_o. Верхняя линия - суммарные издержки (Total Cost). Как видим, точка минимума этих издержек совпадает с точкой, в которой издержки хранения и заказывания совпадают (нижние две линии пересекаются).

Поскольку в предположении этой модели поставка осуществляется мгновенно, а интенсивность  расходования запаса постоянна, то максимальный уровень запаса совпадает с оптимальным и равен 122,47, а его средний уровень составляет половину оптимального и равен 61,24. При этом суммарные издержки запаса равны 1224,74, а число заказов равно D/Q^* = 41 (с округлением).

Рассмотрим вторую модель - модель определения оптимальной партии изделий. При определении оптимальной партии изделий предполагается, что заказ поступает не мгновенно, а постепенно, с постоянной интенсивностью p, а запас расходуется с интенсивностью d, при чем, p > d и, следовательно, пополнение запаса происходит с интенсивностью (p – d). За счет того, что запас одновременно пополняется и расходуется