






























Отрицательная мотивация к познавательной деятельности, к процессу и содержанию учения. 37,7 % |
Низкий уровень активности, познавательная инертность. Отсутствие стремления к деятельности в процессе познания. 33,4 % |
|||
|
Средний уровень. 34,9 % |
Эпизодическая активность, побуждаемая внешними стимулами (учителем, друзьями, родителями, способами выполнения заданий и т. д.). 36,5 % |
Неустойчивая мотивация к внешним сторонам деятельности. Эпизодическая познавательная мотивация с условием внешнего стимулирования. 31,9 % |
Ситуативная самостоятельность в познавательной деятельности. Проявление самостоятельности при наличии внешних побудителей. 41,4 % |
|
|
Высокий уровень. 17,4 % |
Активность, стимулируемая не только внешними, но и внутренними побудителями. 30,5 % |
Устойчивая потребность в познавательной деятельности. Интерес к результату и оценке познавательной деятельности как мотив. 24,1 % |
Интенсивный процесс самостоятельной деятельности по развитию интереса. Стремление использовать помощь. 10,3 % |
|
Почти у половины класса (46,5 %) низкий уровнь развития познавательного интереса; у 34,9 % класса - средние уровни; 17,4 % части класса высокий уровнь развития познавательного интереса; Следовательно, уровнь развития познавательного интереса детей в целом по классу мал, он требует повышения.
Проанализировав полученные результаты мы пришли к выводу, что в классе менее всего сформированны сосредоточенность внимания и стремление поделиться новой информацией.
2.2 Включение в учебный процесс игр по математике, направленных на формирование у учащихся 3 класса познавательного интереса
На основе результатов,полученных на констатирующем этапе мы пришли к выводу о необходимости развития у учащихся 3 класса таких компонентов познавательного интереса как сосредоточенность внимания и стремление поделиться новой информацией.
С этой целью мы разработали программу использования дидактических игр на уроках математики. Данный класс обучается по учебнику «Математика»2004 года, программы по математике для 3 класса автора Моро М. И.2005г. Программа расчитана на 4 часов в неделю.
Программа включения дидактических игр в уроки математике
|
Тема урока |
Математическая игра |
Компоненты познавательного интереса |
|
1 Задачи на увеличение числа в несколько раз |
математический бой |
Устойчивость интереса Сосредотосенность внимания |
|
2 Задачи на уменьшение числа в несколько раз. «меньше на … раз», «уменьшить в … раз» |
математическая мини-игра |
Устойчивость интереса Сосредотосенность внимания |
|
3Решение задач на уменьшение числа в несколько раз |
математические мини-игры |
Сосредотосенность внимания |
|
4 Умножение пяти, на 5 и соответствующие случаи деления |
математический лабиринт |
Сосредоточенность внимания |
|
5 Задачи на кратное сравнение |
||
|
6 Задачи на кратное сравнение |
математические мини-игры |
Сосредоточенность внимания |
|
7 Решение задач на разностное и кратное сравнение |
||
|
8 Умножение 6 на 6 и соответствующие случаи деления |
математический лабиринт |
Сосредоточенность внимания |
|
9 Решение задач на приведение к единице |
||
|
10 Решение задач на приведение к единице |
математический лабиринт |
Сосредоточенность внимания |
|
11 Решение задач. Закрепление. |
КВН |
стремление поделиться новой информацией Сосредотосенность внимания Стремление учавствовать в деятельности Устойчивость интереса |
|
12 Умножение 7 на 7 и соответствующие случаи деления |
математический лабиринт |
Сосредоточенность внимания |
Опишем методику включения в учебный процессс математических игр:
На уроке по теме «Задачи на уменьшение числа в несколько раз. «меньше на … раз», «уменьшить в … раз», на этапе закрепление полученных знаний была использована математическая мини-игра(эстафета).
Правила игры:
При решении примеров записывают не ответ, а букву соответствующию этому числу, которая находится под числом.В игре учавствует весь класс. С каждого ряда вызывается по 1 ученику для прохождения одного задания. Тот ряд который решит быстрее все примеры , тот и становится победителем.
40 : 5 + 4 = 94 — 24 + 16= 21 : 3 + 16 =
25 + 6 * 2 = 8+8 : 4 =
10 * 3 + 25= 36 : 3 + 10 =
В итоге выполнения задания должно получится слово МОЛОДЦЫ.
В ходе выполнения этафеты ученикам нобходимо учавствовать сплоченно, ребятам не только требуется сосредодачивать свое внимание на порядке выполнения задания и правильном подсчете,но и формируется такой компонент как устойчивость интереса.
На роке по теме «Умножение пяти, на 5 и соответствующие случаи деления» на этапе актуализации знаний была проведена игра Лабиринт:
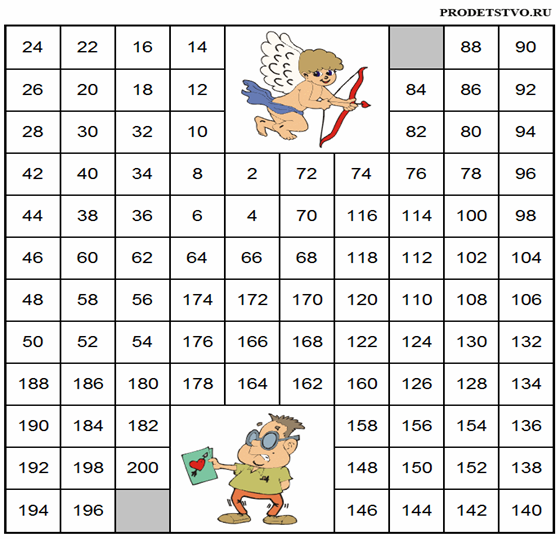 |
Ребята нас сейчас ожидае необычное задание. Нам нужно помочь Амуру попасть в сердце. -А кто из вас знает кто такой Амур?(варианты учеников).
-Правильно! Но что бы Амур попал в сердце, нам нужно бужет пройти по математичесому лабиринту используя числа делящиеся на 5. Нужно будет идти от большего числа к меньшему.(Вызывается ученик к доске.Класс наблюдает )
Молодцы! А кто сможет пройти этот математически лабиринт наоборот?
-Хорошо!
Кто мне сможет рассказать про число 15?(опрос с места).
-Ребята, а какими множителями мы можем представить число 15?
В ходе выполненя задания учащимся необходимо найти путь прохождения по математическому лабиринту. При этом они сосредотачивают свое внимание на порядке действий. Таким образом формируется такой компонент познавательного интереса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.