Погрешности результатов измерений и средств измерений. Метрологическая схема происхождения погрешности результатов измерений

2. ПОГРЕШНОСТИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И СРЕДСТВ ИЗМЕРЕНИЙ

2.1. Метрологическая схема происхождения погрешности результатов

измерений

Происхождение погрешностей результатов прямых измерений иллюстрирует метрологическая структурная схема, приведенная на рис. 2.1.

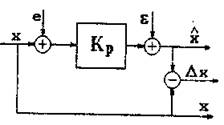
Рис. 2.1. Метрологическая структурная схема образования погрешности результатов измерений

На схеме рис. 2.1 обозначено: х- значение измеряемой величины; - результат прямого измерения; е - обозначение суммарного действия наводок, помех, погрешностей от взаимовлияния средства измерений и объекта измерений, погрешностей, вызванных некорректной постановкой задачи измерений; ε-собственная аддитивная погрешность средства измерений; К_Р- реальный коэффициент преобразования, присущий данному экземпляру средства измерений и отличающийся от идеального коэффициента преобразования, равного 1, не более, чем на нормированное значение погрешности; Δх- погрешность результата прямого измерения.

Из рис. 2.1 непосредственно следует, что формула для абсолютной погрешности результата прямого измерения имеет вид:

Δх = - х = ( К_Р -1 ) ´ х + ε + К_Р ´ е.

Введем обозначение Кр -1 = ΔК. С учетом того, что |ΔК • ε | <<|e|, получим выражение для абсолютной погрешности прямого измерения:

Δх ≈ ΔК -х + ε + е.             (2.1)

Относительная  погрешность  результата  прямого  измерения,  которая обычно выражается в процентах, определяется равенством

      (2.2)

где γ_K  γ_ε   γ_е суть: относительная погрешность коэффициента преобразования по отношению к значению идеального коэффициента, равного 1; относительная аддитивная погрешность средства измерений; относительная погрешность взаимодействия средства измерений с объектом, выраженные в процентах. Помехи, однородные с измеряемой величиной и действующие в сумме с ней на входе, а также внешние помехи входят в состав погрешностей е и ε.

В этих равенствах первые два слагаемые порождены собственными свойствами средства измерений из-за несовершенства технологии изготовления и неизбежного разброса параметров комплектующих изделий, деталей и узлов. По этой причине ΔК х + ε и γ_ε+γ_е называются инструментальными погрешностями (абсолютными и относительными соответственно). Инструментальные погрешности могут изменяться при изменении внешних факторов (климатических, механических и др.), действующих на средство измерений в реальных условиях эксплуатации. Ответственность за инструментальную погрешность несет производитель средства измерений, и поэтому в целях обеспечения надлежащего качества и гарантий для потребителя на инструментальную погрешность назначаются нормы в виде пределов допускаемых значений. Каждый экземпляр средства измерений при выпуске из производства и периодически во время эксплуатации должен контролироваться на предмет удовлетворения этим нормам.

Абсолютная инструментальная погрешность состоит из двух слагаемых. Первое из них, а именно, ΔКх линейно зависит от измеряемой величины и называется мультипликативной абсолютной погрешностью. Второе слагаемое ε не зависит от измеряемой величины и называется аддитивной абсолютной погрешностью. Точно так же слагаемые относительной инструментальной погрешности γ_ε+γ_е называются Мультипликативной относительной погрешностью и аддитивной относительной погрешностью соответственно.

Третьим слагаемым в равенствах (2.1), (2.2) является погрешность, которая возникает только при конкретном применении средства измерений, поэтому она нормироваться не может, ибо производитель не несет за нее ответственность. Для того, чтобы потребитель мог оценить характеристику этой погрешности в конкретных условиях применения, производитель сообщает и гарантирует нормированные характеристики входного сопротивления и иных свойств средства измерений, которые требуются для этого расчета.

В реальных условиях измерений, когда в составе погрешностей ε, и е присутствуют пульсации измеряемой величины и помехи, когда на средство азме рений действуют различные трудно учитываемые внешние факторы, а собственно средство измерений содержит внутренние источники случайного шума, тогда в общей погрешности измерений появляются случайные составляющие. Они проявляются в разбросе значений результатов многократных измерений неизменной во времени величины.

Альтернативой случайной составляющей погрешности средств измерений и результатов измерений является систематическая составляющая, которая порождается систематической составляющей аддитивной погрешности е, погрешностью коэффициента преобразования и взаимодействием средства измерений с объектом, а также паразитными медленно меняющимися сигналами, такими, как например, термоЭДС в измерительных цепях.

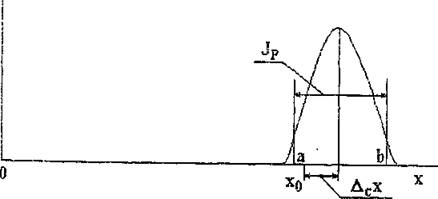Для иллюстрации сказанного на рис. 2.2 приведен пример возможного распределения большого количества результатов измерений неизменной величины х. Принято, что истинное значение измеряемой величины равно х₀ и что измерения сопровождаются систематической погрешностью Дсх, причем в этом случае Δ_с> 0 , Плотность разброса результатов измерений, вызванного случайной составляющей погрешности, показана колоколообразной кривой.

Из общих соображений понятно, что значение погрешности каждого конкретного результата измерений знать невозможно, ибо в противном случае можно было бы определить точное истинное значение измеряемой величины простым введением поправки на эту погрешность. Поэтому на практике пользуются характеристиками погрешности. Наиболее распространенными среди них являются:

-    характеристики случайной составляющей:

а)   среднеквадратическое значение случайной составляющей погрешности