Овладение статистическими методами обработки результатов многократных измерений неизменной во времени величины в условиях действия случайных погрешностей и помех с целью повышения точности результата измерений, страница 2

5.2. Пункт 4.2. программы работы.

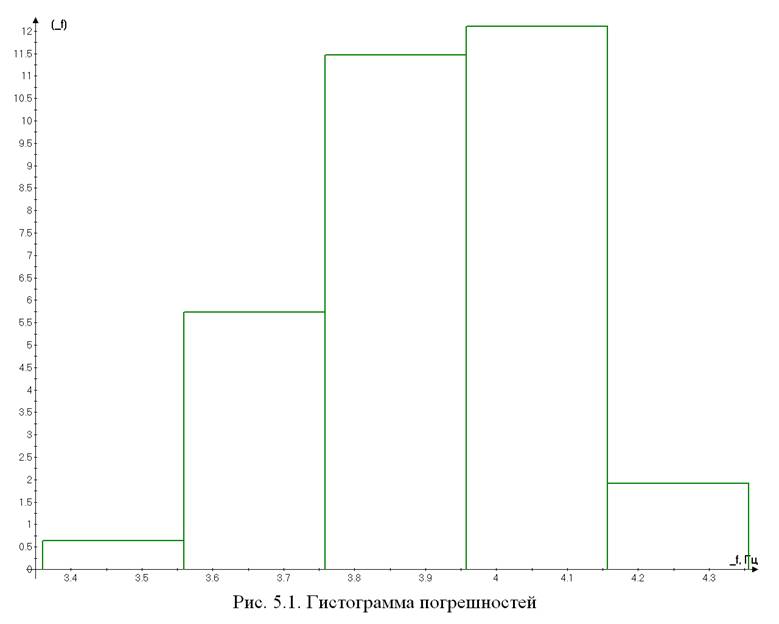
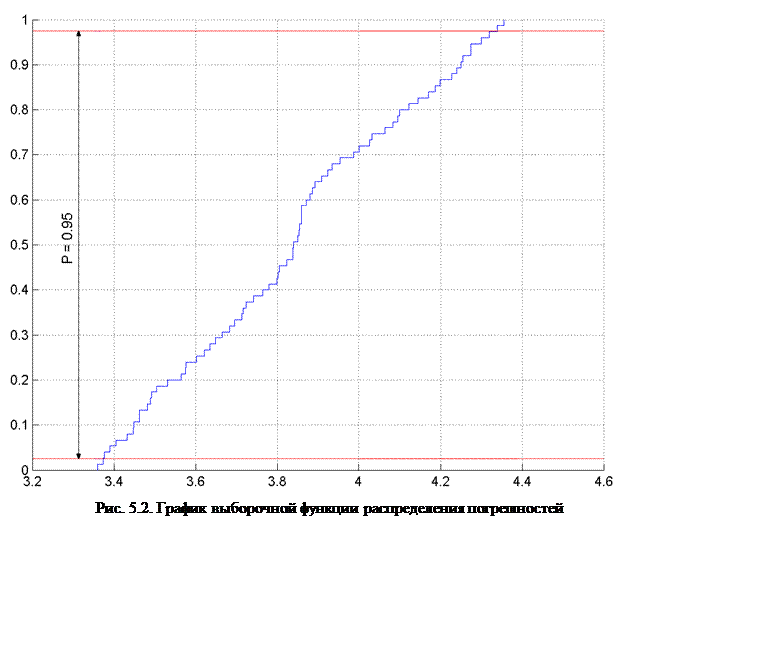
С помощью программы laba1_6_3.exe были построены графики гистограммы и выборочной функции распределения (рис. 5.1 и 5.2) на основе измерений приведенных в предыдущем пункте.

Минимальное значение:     0 кГц

Выборочная медиана:         0,589023 кГц

Максимальное значение:    0,589023 кГц

Среднее значение:               0,581169 кГц

Средина размаха:                 0,294511 кГц

С.К.О.:                                   0,068014 кГц

Исходным материалом для обработки послужили выборочные значения (Таблица 5.1), из которых затем был составлен вариационный ряд. По этим значениям построены выборочная функция распределения и гистограмма, которые послужили для оценки характеристик случайных составляющих погрешности.

5.3. Пункт 4.3. программы работы.

Таблица 5.2. Результаты проведенных ЭВМ вычислений

Границы доверительных интервалов случайны. Для математического ожидания они оцениваются по формулам: , где  и  - точечные оценки систематической составляющей и среднеквадратического значения случайной составляющей погрешности измерения соответствующего параметра, Q – заданная доверительная вероятность. В нашем случае Q = 0,95.

Вычисление границ доверительного интервала для среднеквадратического значения случайной составляющей погрешности основано на том, что если плотность распределения случайной составляющей погрешности нормальна, то плотность распределения величины:

Поскольку погрешности нормируются и предоставляются интервалами J_p, симметричными относительно нуля, то доверительные интервалы для них будут так же симметричными.

Выводы.

Исходя из вышесказанного, можно сделать вывод о наличии аддитивной и мультипликативной составляющих погрешности.

Аддитивная погрешность вызывает сдвиг измеряемой величины вдоль оси ординат. Отсюда мы и сделали вывод о ее наличии, так как значения вариационного ряда (полученные в результате выполнения программы laba1_6_4.exe) сдвинуты влево относительно измеренных значений. Аддитивная погрешность постоянна при всех значениях измеряемой величины. Эта погрешность могла быть вызвана контактными сопротивлениями, случайными и периодическими колебаниями в выходном сигнале и т. п.

О наличии мультипликативной погрешности сделали вывод из того, что она линейно зависит от измеряемой величины, то есть если она зависит, то она соответственно и присутствует в данной погрешности.

Вследствие провидения лабораторной работы нами не был получен вид закона распределения, из–за неработоспособности программного обеспечения, поэтому вывод о нем мы сделать не можем.