Метрология цвета. Общие сведения. Первый, второй и третий законы Грассмана. Вектор цвета в произвольной цветовой координатной системе

Пусть для получения цвета F надо взять r' таких новых единиц цвета R, g' единиц цвета G и b' единиц цвета В.

Это мы запишем в виде равенства:

Вспоминая опять, что цвет зависит только от относительного количества компонентов, а не от их абсолютных величин, заменим числа r', g' , b' их относительными долями в общей смеси, которые обозначим через r, g и b:

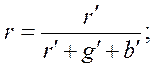
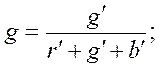
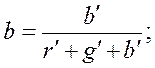
причем, очевидно, должно быть

.

Числа r, g и b, выражающие доли красного, зеленого и синего единичных цветов в данной смеси, называются трехцветными коэффициентами. Они служат выражением цвета в описываемой трехцветной системе.

Тот факт, что данный цвет F составляется из r долей единичного основного цвета R, g долей цвета G и b долей цвета В, записывают в форме цветового уравнения   вида

Из законов Грассмана следует, что цвет можно выразить точкой в трехмерном пространстве. Трехмерное пространство для геометрического изображения цвета принято называть цветовым пространством. В нем каждому цвету будет соответствовать определенная точка, а каждой точке пространства – соответствующий цвет.

В цветовой системе координат каждый цвет выражается через основные цвета этой системы, причем они должны быть линейно независимы (то есть ни один из них не должен получаться сложением двух других). Положение точки в пространстве, характеризующей тот или иной цвет, задается тремя координатами. Эту же точку можно рассматривать и как конец вектора, проведенного из начала координат (рис. 2.1).

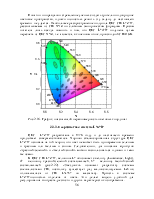
Для того чтобы процесс трехкомпонентного цветосмешения был более интуитивно понятен, его можно изобразить на трехмерном графике, оси которого образованы тремя основными цветами R, G и B (рис. 2.2). В прямоугольной системе координат это построение реализуется в виде так называемого цветового куба.

В цветовом кубе грани  образованы координатами R, G, B, а вершины соответствуют положению чистых цветов: красного, зеленого, синего и образуемых в результате их смешения желтого, пурпурного и голубого. Точка начала координат осей R, G, B соответствует положению черного цвета. Напротив него располагается белый цвет, образуемый смешением чистых красного, зеленого и синего цветов, а линия K–W представляет собой ось нейтральных цветов. Цвет А, показанный на графике, задается следующими координатами: R = 0,8 , G = 0,2, B = 0,6.

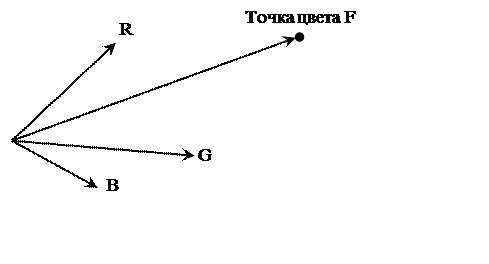
Рис. 2.1. Вектор цвета в произвольной цветовой координатной системе

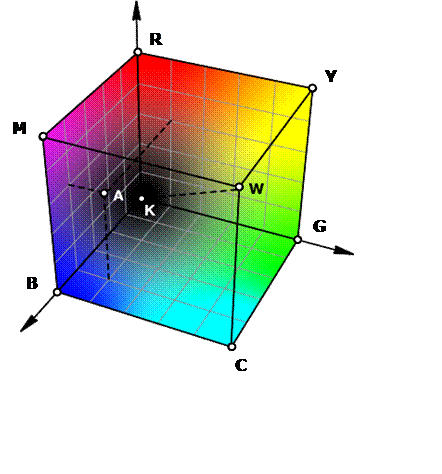
Рис. 2.2. Цветовой график трехкоординатного цветового пространства

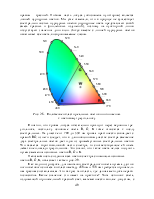
Однако еще Максвелл заметил, что для описания цветности нет необходимости прибегать к пространственным представлениям. Достаточно использовать плоскость треугольника цветности (рис. 2.3).

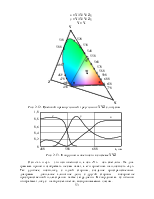
Максвелл значительно упростил этот график, вычертив его на плоскости в виде треугольника, представляющего собой проекцию точек трехмерного цветового графика на одной плоскости. Полученное им построение называется цветовым треугольником Максвелла (рис. 2.4). Он представляет собой равносторонний треугольник вершины которого соответствуют координатам основных красного, зеленого и синего цветов. Фактически этот треугольник представляет собой график цветностей цветового тела RGB. Значение яркости (светлоты) света в нем не учитывается.

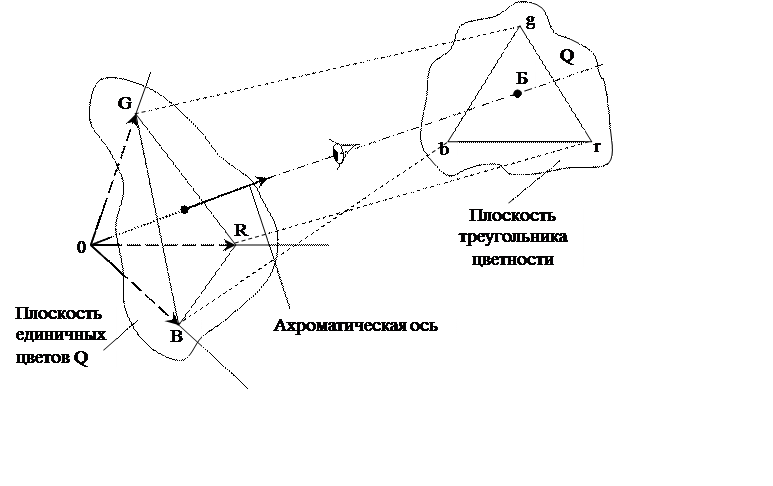
Рис. 2.3. Плоскость единичных цветов и образование треугольника цветности

Вершины треугольника соответствуют положению трех основных цветов: красного (R), зеленого (G) и синего (B). В центрах сторон треугольника распологаются дополнительные желтый (Y), пурпурный (C) и голубой цвета (М), а в точке пересечения перпендекуляров восстановленных от сторон треугольника находится белый цвет (W), задаваемый координатами цветности r = g = b = 1/3. На линиях W–R, W–G, W–B располагаются красные, зеленые и синие цвета, а на линиях W–C, W–M, W–Y – дополнительные им желтый, пурпурный и голубой цвета по степени увеличения их насыщенности. Цвет A1 определяется координатами цветности r = 0.1, g = 0.2 и получается смешением красного, зеленого и синего цветов