Графики плотностей распределения и предельных и действующих напряжений. Вероятность отказа вала по критерию сопротивления усталости за усталостное время, страница 2

=  =  = 90 МПа                                          (5)

5.  Среднее значение действующих напряжений

 = = 0,65772 =502 МПа.

Среднее квадратическое отклонение действующих напряжений

=  = 0,15502 = 76 МПа

6.  Плотность вероятности нормального распределения случайной величины x определяется по формуле

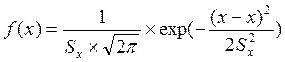                                         (6)

Если в выражении (6) перейти к новой переменной, называемой нормированной случайной величиной (см. табл. III [7. c.206]),

                                                             (7)

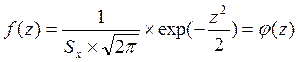тогда                                                                    (8)

          Выражение (8) является плотностью вероятностей нормированного нормального распределения. Значения этой функции приведены в [8. c.80].

Пользуясь значениями для , удобно вычислять значения плотности вероятностей f(x):

                                                     (9)

Для построения функций плотности вероятностей ,  предельных  и действующих  напряжений необходимые расчеты будем производить в табличной форме (табл. 3, [3. c.22]). В первой колонке табл. 3 задаемся значениями квантилей в диапазоне [-3,09; 3,09]. Во второй - записываем значения вероятностей Р, соответствующие квантилям  первой колонки, пользуясь табл. III [7]. В третью и четвертую колонки заносим значения пределов выносливости  и действующих напряжений , определяемых по уравнениям (5) и

                                                             (10)

В следующей, пятой колонке записываем значения нормированной функции  нормального распределения, определяемые с помощью таблицы [8. с.80]

Заметим, что  - четная функция, т.е. .

Численные значения функций  и  заносим в последние две колонки табл. 3. Они определяются по формуле (9). По данным табл. 3 строим графики функций  и , изображенные на рисунке 4.

Таблица 3 – Расчет функций плотностей распределения  и

zp	P	, МПа	, МПа
-3,0	0,001	502	274	0,0043	0,000047	0,000056
-2,5	0,006	547	312	0,0175	0,000200	0,000220
-2,0	0,023	592	350	0,0540	0,000600	0,000700
-1,5	0,067	637	388	0,1295	0,001400	0,001700
-1,0	0,159	682	426	0,2420	0,003000	0,003000
-0,5	0,309	727	464	0,3521	0,004000	0,004500
0	0,500	772	502	0,3989	0,005000	0,005200
0,5	0,691	817	540	0,3521	0,004000	0,004500
1,0	0,841	862	578	0,2420	0,003000	0,003000
1,5	0,933	907	616	0,1295	0,001400	0,001700
zp	P	, МПа	, МПа
2,0	0,977	952	654	0,0540	0,000600	0,000700
2,5	0,994	997	692	0,0175	0,000200	0,000220
3,0	0,999	1042	730	0,0043	0,000047	0,000056

7.  Как видно из рис. 2, верхняя граница рассеяния 730 МПа действующих напряжений оказалась больше нижней границы рассеяния пределов выносливости  495 МПа). Следовательно, существует вероятность отказа вала F, равная площади, заштрихованной на рис. 2. Для аналитического определения вероятности отказа F предложено выражение:

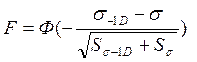                                                 (11)

где   Ф – интегральная функция распределения нормированной случайной величины (функция Лапласа), значения которой приведены в приложении 1 (табл. П.7 [3. с.53]). Следует иметь в виду, что эта функция является нечетной, т.е. Ф(-х) = 1 – Ф(х). В нашем случае вероятность отказа вала

Рисунок 4 – Интегральные функции распределения пределов выносливости

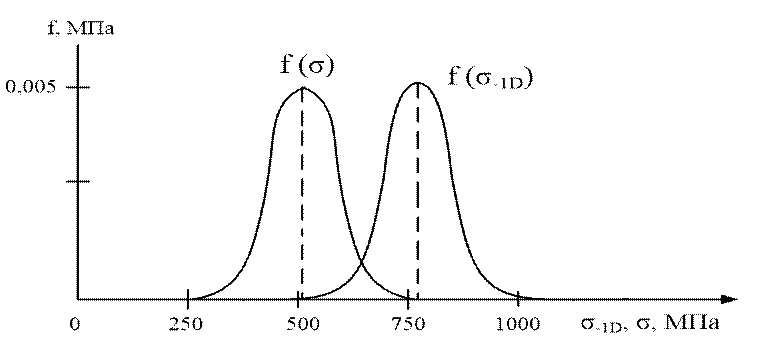
Рисунок 5 – Функции плотности вероятностей fи f